青海省中考数学真题汇编(近几年)3 函数
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 若 , 是函数 图象上的两点,当 时,下列结论正确的是( )
A、 B、 C、 D、2. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 A、
A、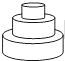 B、
B、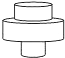 C、
C、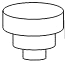 D、
D、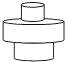 3. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、
3. 若 ,则正比例函数 与反比例函数 在同一平面直角坐标系中的大致图象可能是( )A、 B、
B、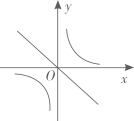 C、
C、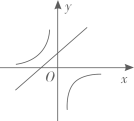 D、
D、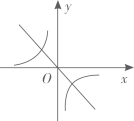 4. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( )
4. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( ) A、
A、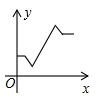 B、
B、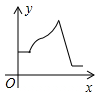 C、
C、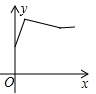 D、
D、
二、填空题
-
5. 已知点 在第四象限,则m的取值范围是 .6. 已知点 和点 在反比例函数 的图象上,则 与 的大小关系是 .7. 函数 中自变量x的取值范围是 .
8. 根据如图所示的程序,计算 的值,若输入 的值是1时,则输出的 值等于.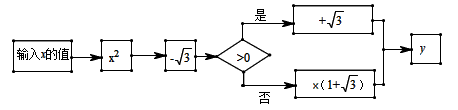 9. 如图, 是反比例函数 图象上的一点,过点 向 轴作垂线交于点 ,连接 .若图中阴影部分的面积是1,则此反比例函数的解析式为.
9. 如图, 是反比例函数 图象上的一点,过点 向 轴作垂线交于点 ,连接 .若图中阴影部分的面积是1,则此反比例函数的解析式为.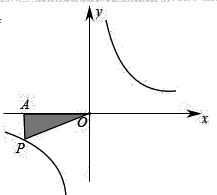
三、综合题
-
10. 如图,在平面直角坐标系中,直线 与坐标轴交于 两点,点 在 轴上,点 在 轴上, 点的坐标为 ,抛物线 经过点 .
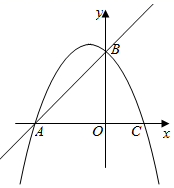 (1)、求抛物线的解析式;(2)、根据图象写出不等式 的解集;(3)、点 是抛物线上的一动点,过点 作直线 的垂线段,垂足为 点,当 时,求P点的坐标.11. 如图1(注:与图2完全相同)所示,抛物线 经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C.
(1)、求抛物线的解析式;(2)、根据图象写出不等式 的解集;(3)、点 是抛物线上的一动点,过点 作直线 的垂线段,垂足为 点,当 时,求P点的坐标.11. 如图1(注:与图2完全相同)所示,抛物线 经过B、D两点,与x轴的另一个交点为A,与y轴相交于点C. (1)、求抛物线的解析式.(2)、设抛物线的顶点为M,求四边形ABMC的面积(请在图1中探索)(3)、设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标(请在图2中探索)12. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点 、 、 三点.
(1)、求抛物线的解析式.(2)、设抛物线的顶点为M,求四边形ABMC的面积(请在图1中探索)(3)、设点Q在y轴上,点P在抛物线上.要使以点A、B、P、Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标(请在图2中探索)12. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点 、 、 三点. (1)、求抛物线的解析式和对称轴;(2)、 是抛物线对称轴上的一点,求满足 的值为最小的点 坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点 E ,使四边形 OEBF 是以 OB 为对角线且面积为12的平行四边形?若存在,请求出点 E 坐标,若不存在请说明理由(请在图2中探索)
(1)、求抛物线的解析式和对称轴;(2)、 是抛物线对称轴上的一点,求满足 的值为最小的点 坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点 E ,使四边形 OEBF 是以 OB 为对角线且面积为12的平行四边形?若存在,请求出点 E 坐标,若不存在请说明理由(请在图2中探索)
13. 如图,抛物线 与坐标轴交点分别为 , , ,作直线BC.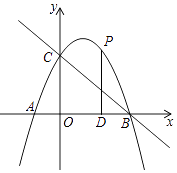 (1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.
(1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.