云南省中考数学真题汇编（近几年）6 统计与概率

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列判断正确的是（）

A、北斗系统第五十五颗导航卫星发射前的零件检查，应选择抽样调查 B、一组数据6，5，8，7，9的中位数是8 C、甲、乙两组学生身高的方差分别为S_甲²＝2.3，S_乙²＝1.8.则甲组学生的身高较整齐 D、命题“既是矩形又是菱形的四边形是正方形”是真命题

查看试题解析
2. 下列说法正确的是（）

A、为了解三名学生的视力情况，采用抽样调查 B、任意画一个三角形，其内角和是 $360 °$ 是必然事件 C、甲、乙两名射击运动员10次射击成绩（单位：环）的平均数分别为 $\bar{x_{甲}}$ 、 $\bar{x_{乙}}$ ，方差分别为 S_甲² 、 S_乙² .若 $\bar{x_{甲}} = \bar{x_{乙}}$ ， S_甲² =0.4 ， S_乙²⁼² ，则甲的成绩比乙的稳定 D、一个抽奖活动中，中奖概率为 $\frac{1}{20}$ ，表示抽奖20次就有1次中奖

查看试题解析
3. 2020年以来，我国部分地区出现了新冠疫情．一时间，疫情就是命令，防控就是责任，一方有难八方支援，某公司在疫情期间为疫区生产A、B、C、D四种型号的帐篷共20000顶，有关信息见如下统计图：

下列判断正确的是（）

A、单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍 B、单独生产B型帐篷的天数是单独生产A型帐篷天数的1.5倍 C、单独生产A型帐篷与单独生产D型帐篷的天数相等 D、每天单独生产C型帐篷的数量最多

查看试题解析
4. 下列判断正确的是（）

A、甲乙两组学生身高的平均数均为1.58，方差分别为S_甲²=2.3，S_乙²=1.8，则甲组学生的身高较整齐 B、为了了解某县七年级4000名学生的期中数学成绩，从中抽取100名学生的数学成绩进行调查，这个问题中样本容量为4000 C、在“童心向党，阳光下成长”合唱比赛中，30个参赛队的决赛成绩如下表：
比赛成绩/分 9.5 9.6 9.7 9.8 9.9
参赛队个数 9 8 6 4 3
则这30个参赛队决赛成绩的中位数是9.7 D、有13名同学出生于2003年，那么在这个问题中“至少有两名同学出生在同一个月”属于必然事件

查看试题解析
5. 2017年12月8日，以“[数字工匠]玉汝于成，[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节•玉溪暨第10届全国三维数字化创新设计大赛（简称“全国3D大赛”）总决赛在玉溪圆满闭幕．某学校为了解学生对这次大赛的了解程度，在全校1300名学生中随机抽取部分学生进行了一次问卷调查，并根据收集到的信息进行了统计，绘制了下面两幅统计图．下列四个不符合题意的是（）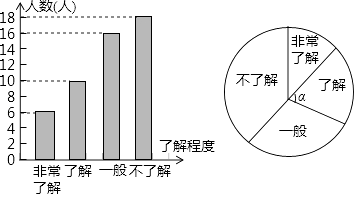

A、抽取的学生人数为50人 B、“非常了解”的人数占抽取的学生人数的12% C、a=72° D、全校“不了解”的人数估计有428人

查看试题解析

二、填空题

6. 某中学九年级甲、乙两个班参加了一次数学考试，考试人数每班都为40人，每个班的考试成绩分为A、B、C、D、E五个等级，绘制的统计图如下：

根据以上统计图提供的信息，则D等级这一组人数较多的班是

查看试题解析

7. 某公司员工的月工资如下：

员工	经理	副经理	职员A	职员B	职员C	职员D	职员E	职员F	杂工G
月工资/元	7000	4400	2400	2000	1900	1800	1800	1800	1200

经理、职员C、职员D从不同的角度描述了该公司员工的收入情况.设该公司员工的月工资数据（见上述表格）的平均数、中位数、众数分别为k、m、n，请根据上述信息完成下列问题：

(1)、

k =

，

m =

，

n =

；

(2)、上月一个员工辞职了，从本月开始，停发该员工工资.若本月该公司剩下的8名员工的月工资不变，但这8名员工的月工资数据（单位：元）的平均数比原9名员工的月工资数据（见上述表格）的平均数减小了.你认为辞职的那名员工可能是.

查看试题解析

三、综合题

8. 为庆祝中国共产党成立100周年，某市组织该市七、八两个年级学生参加演讲比赛，演讲比赛的主题为“追忆百年历程，凝聚青春力量”该市一中学经过初选，在七年级选出3名同学，其中2名女生，分别记 $x_{1}$ 、 $x_{2}$ ，1名男生，记为 $y_{1}$ ；在八年级选出3名同学，其中1名女生，记为 $x_{3}$ ，2名男生，分别记为 $y_{2}$ 、 $y_{3}$ ．现分别从两个年级初选出的同学中，每个年级随机选出一名同学组成代表队参加比赛．

(1)、用列表法或树状图法（树状图也称树形图）中的一种方法，求所有可能出现的代表队总数；

(2)、求选出的代表队中的两名同学恰好是一名男生和一名女生的概率P ．

查看试题解析
9. 有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，4，6；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球.小杰先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），小玉再从瓶子中随机取出一个小球，记下小球上的数字.

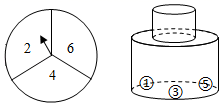(1)、请用列表或画树状图的方法（选其中一种）表示出所有可能出现的结果；

(2)、若得到的两数字之和是3的倍数，则小杰赢；若得到的两数字之和是7的倍数，则小玉赢，此游戏公平吗？为什么？

查看试题解析
10. 甲、乙两个家庭来到以“生态资源，绿色旅游”为产业的美丽云南，各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪个城市旅游不受任何因素影响，上述三个城市中的每一个被选到的可能性相同，甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为 $P$ .

(1)、直接写出甲家庭选择到大理旅游的概率；

(2)、用列表法或树状图法（树状图也称树形图）中的一种方法，求 $P$ 的值.

查看试题解析
11. 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：

月销售量/件数

1770

480

220

180

120

90

人数

1

1

3

3

3

4

(1)、直接写出这15名营业员该月销售量数据的平均数、中位数、众数；

(2)、如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由.

查看试题解析
12. 甲、乙两名同学玩一个游戏：在一个不透明的口袋中装有标号分别为1，2，3，4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球，记下标号后放回口袋中，充分摇匀后，再从口袋中随机摸出一个小球，记下该小球的标号，两次记下的标号分别用x、y表示.若x＋y为奇数，则甲获胜；若x＋y为偶数，则乙获胜.

(1)、用列表法或树状图法(树状图也称树形图)中的一种方法，求(x，y)所有可能出现的结果总数；

(2)、你认为这个游戏对双方公平吗？请说明理由.

查看试题解析
13. 某初级中学数学兴趣小组为了了解本校学生的年龄情况，随机调查了该校部分学生的年龄，整理数据并绘制如下不完整的统计图．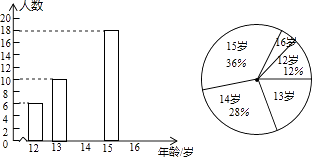
依据以上信息解答以下问题：

(1)、求样本容量；

(2)、直接写出样本容量的平均数，众数和中位数；

(3)、若该校一共有1800名学生，估计该校年龄在15岁及以上的学生人数．

查看试题解析
14. 数学课上，李老师准备了四张背面看上去无差别的卡片A，B，C，D，每张卡片的正面标有字母a，b，c表示三条线段（如图），把四张卡片背面朝上放在桌面上，李老师从这四张卡片中随机抽取一张卡片后不放回，再随机抽取一张．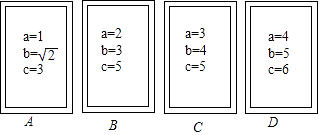

(1)、用树状图或者列表表示所有可能出现的结果；

(2)、求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率．

查看试题解析
15. 近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：

(1)、本次一共调查了多少名购买者？

(2)、请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为度．

(3)、若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？

查看试题解析
16. 为了促进“足球进校园”活动的开展，某市举行了中学生足球比赛活动现从A，B，C三支获胜足球队中，随机抽取两支球队分别到两所边远地区学校进行交流．

(1)、请用列表或画树状图的方法（只选择其中一种），表示出抽到的两支球队的所有可能结果；

(2)、求出抽到B队和C队参加交流活动的概率．

查看试题解析
17. 某同学参加了学校举行的“五好小公民•红旗飘飘”演讲比赛，7名评委给该同学的打分（单位：分）情况如下表：
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8

(1)、直接写出该同学所得分数的众数与中位数；

(2)、计算该同学所得分数的平均数

查看试题解析
18. 将正面分别写着数字1，2，3的三张卡片（注：这三张卡片的形状、大小、质地，颜色等其他方面完全相同，若背面上放在桌面上，这三张卡片看上去无任何差别）洗匀后，背面向上放在桌面上，从中先随机抽取一张卡片，记该卡片上的数字为x，再把剩下的两张卡片洗匀后，背面向上放在桌面上，再从这两张卡片中随机抽取一张卡片，记该卡片上的数字为y．

(1)、用列表法或树状图法（树状图也称树形图）中的一种方法，写出（x，y）所有可能出现的结果．

(2)、求取出的两张卡片上的数字之和为偶数的概率P．

查看试题解析

19. 某鞋店在一周内销售某款女鞋，尺码（单位：cm）数据收集如下：

24 23.5 21.5 23.5 24.5 23 22 23.5 23.5 23 22.5 23.5 23.5 22.5 24 24 22.5 25 23 23 23.5 23 22.5 23 23.5 23.5 23 24 22 22.5

绘制如图不完整的频数分布表及频数分布直方图：

尺码/cm	划记	频数
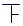
21.5≤x＜22.5		3
22.5≤x＜23.5
23.5≤x＜24.5		13
24.5≤x＜25.5		2

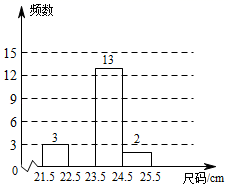(1)、请补全频数分布表和频数分布直方图；

(2)、若店主要进货，她最应该关注的是尺码的众数，上面数据的众数为

(3)、若店主下周对该款女鞋进货120双，尺码在23.5≤x＜25.5范围的鞋应购进约多少双？

查看试题解析

20. 垃圾的分类回收不仅能够减少环境污染，美化家园，甚至能够变废为宝，节约能源，为增强学生垃圾分类意识，推动垃圾分类进校园，某中学组织全校1565名学生参加了“垃圾分类知识竞赛”（满分为100分），该校数学兴趣小组为了解全校学生竞赛分数情况，采用简单随机抽样的方法（即每名学生的竞赛分数被抽到的可能性相等的抽样方法）抽取部分学生的竞赛分数进行调查分析．

(1)、以下三种抽样调查方案：

方案一：从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本；

方案二：从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本；

方案三：从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本，其中抽取的样最具有代表性和广泛性的一种抽样调查方案是（填写“方案一”、“方案二”或“方案三”）；

(2)、该校数学兴趣小组根据简单随机抽样方法获得的样本，绘制出如下统计表（90分及以上为“优秀”，60分及以上为“及格”，学生竞赛分数记为x分）

样本容量		平均分			及格率			优秀率	最高分	最低分
100		83.59			95%			40%	100	52
分数段	$50 \leq x < 60$		$60 \leq x < 70$	$70 \leq x < 80$		$80 \leq x < 90$	$90 \leq x \leq 100$
频数	5		7	18		30	40

结合上述信息解答下列问题：

①样本数据的中位数所在分数段为；

②全校1565名学生，估计竞赛分数达到“优秀”的学生有人．

查看试题解析

评委	评委1	评委2	评委3	评委4	评委5	评委6	评委7
打分	6	8	7	8	5	7	8

比赛成绩/分	9.5	9.6	9.7	9.8	9.9
参赛队个数	9	8	6	4	3

月销售量/件数	1770	480	220	180	120	90
人数	1	1	3	3	3	4