云南省中考数学真题汇编(近几年)5 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 由5个完全相同的正方体组成的几何体的主视图是( )
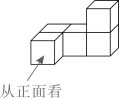 A、
A、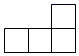 B、
B、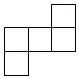 C、
C、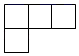 D、
D、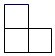 2. 下列几何体中,主视图是长方形的是( )A、
2. 下列几何体中,主视图是长方形的是( )A、 B、
B、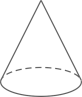 C、
C、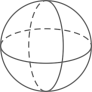 D、
D、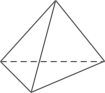 3. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
3. 下列图形既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为( )
4. 如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为( ) A、
A、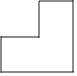 B、
B、 C、
C、 D、
D、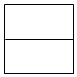 5. 下列几何体的左视图为长方形的是( )A、
5. 下列几何体的左视图为长方形的是( )A、 B、
B、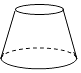 C、
C、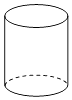 D、
D、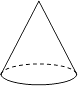 6. 下列图形既是轴对称图形,又是中心对称图形的是( )A、三角形 B、菱形 C、角 D、平行四边形7. 下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
6. 下列图形既是轴对称图形,又是中心对称图形的是( )A、三角形 B、菱形 C、角 D、平行四边形7. 下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )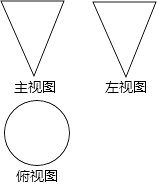 A、三棱柱 B、三棱锥 C、圆柱 D、圆锥8. 在 中, ,若 ,则 的长是( )A、 B、 C、60 D、809. 如图,在平面直角坐标系中,将△OAB(顶点为网格线交点)绕原点O顺时针旋转90°,得到△OA′B′,若反比例函数y= 的图象经过点A的对应点A′,则k的值为( )
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥8. 在 中, ,若 ,则 的长是( )A、 B、 C、60 D、809. 如图,在平面直角坐标系中,将△OAB(顶点为网格线交点)绕原点O顺时针旋转90°,得到△OA′B′,若反比例函数y= 的图象经过点A的对应点A′,则k的值为( )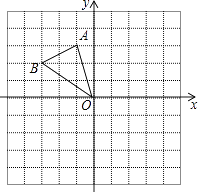 A、-6 B、﹣3 C、3 D、610. 如图,点A在双曲线y═ (x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于 OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为( )
A、-6 B、﹣3 C、3 D、610. 如图,点A在双曲线y═ (x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于 OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为( ) A、2 B、 C、 D、11. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )
A、2 B、 C、 D、11. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )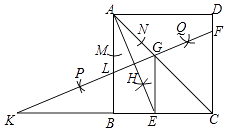 A、①②③ B、②③④ C、①③④ D、①②④12. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A、①②③ B、②③④ C、①③④ D、①②④12. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )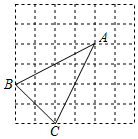 A、4个 B、5个 C、6个 D、7个
A、4个 B、5个 C、6个 D、7个二、填空题
-
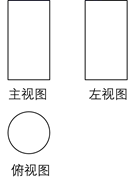
13. 如图是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为 .
 14. 如图,已知AB∥CD,若 ,则 = .
14. 如图,已知AB∥CD,若 ,则 = . 15. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .16. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .
15. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .16. 如图,在 中,点D , E分别是 的中点, 与 相交于点F , 若 ,则 的长是 .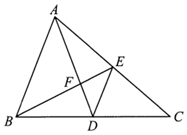
三、解答题
-
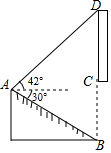
17. 小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=6.5m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90, ≈1.73)
四、综合题
-
18. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .
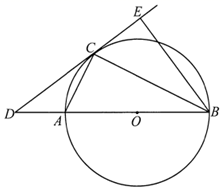 (1)、求证: 是 的切线:(2)、若 ,求 的长.19. (材料阅读)2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个规标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为f= (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.
(1)、求证: 是 的切线:(2)、若 ,求 的长.19. (材料阅读)2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上立一个规标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于300m时,还要考虑球气差,球气差计算公式为f= (其中d为两点间的水平距离,R为地球的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.(问题解决)某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,点A,B的水平距离d=800m,测量仪AC=1.5m,觇标DE=2m,点E,D,B在垂直于地面的一条直线上,在测量点A处用测量仪测得山项觇标顶端E的仰角为37°,测量点A处的海拔高度为1800m.
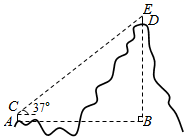 (1)、数据6400000用科学记数法表示为;(2)、请你计算该山的海拔高度.(要计算球气差,结果精确到0.01m)
(1)、数据6400000用科学记数法表示为;(2)、请你计算该山的海拔高度.(要计算球气差,结果精确到0.01m)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
20. 如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.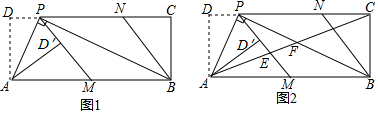 (1)、求证:AD2=DP•PC;(2)、请判断四边形PMBN的形状,并说明理由;(3)、如图2,连接AC,分别交PM,PB于点E,F.若 = ,求 的值.21. 如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点.
(1)、求证:AD2=DP•PC;(2)、请判断四边形PMBN的形状,并说明理由;(3)、如图2,连接AC,分别交PM,PB于点E,F.若 = ,求 的值.21. 如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点. (1)、求证:四边形AEFD是矩形;(2)、如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF上时,则有OB=OM.请说明理由;(3)、如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,DM,当△AMD是等腰三角形时,求AP的长.
(1)、求证:四边形AEFD是矩形;(2)、如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF上时,则有OB=OM.请说明理由;(3)、如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,DM,当△AMD是等腰三角形时,求AP的长.
-