云南省中考数学真题汇编(近几年)4 图形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 一个十二边形的内角和等于( )A、2160° B、2080° C、1980° D、1800°2. 下列判断正确的是( )A、北斗系统第五十五颗导航卫星发射前的零件检查,应选择抽样调查 B、一组数据6,5,8,7,9的中位数是8 C、甲、乙两组学生身高的方差分别为S甲2=2.3,S乙2=1.8.则甲组学生的身高较整齐 D、命题“既是矩形又是菱形的四边形是正方形”是真命题3. 一个十边形的内角和等于( )A、 B、 C、 D、4. 如图,直线c与直线a、b都相交.若 , ,则 ( )
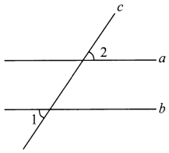 A、 B、 C、 D、5. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )
A、 B、 C、 D、5. 如图,等边 的三个顶点都在 上, 是 的直径.若 ,则劣弧 的长是( )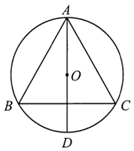 A、 B、 C、 D、6. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A、 B、 C、 D、6. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、7. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )
A、 B、1 C、 D、7. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )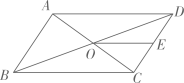 A、 B、 C、 D、8. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A、 B、 C、 D、8. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )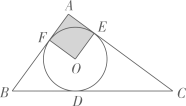 A、4 B、6.25 C、7.5 D、99. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( )A、48π B、45π C、36π D、32π10. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )
A、4 B、6.25 C、7.5 D、99. 一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的全面积是( )A、48π B、45π C、36π D、32π10. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )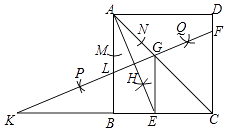 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
11. 如图,直线c与直线a、b都相交.若 ∥ , ,则 度.
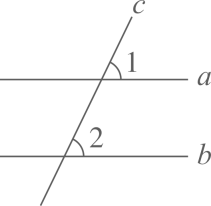 12. 如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为°.
12. 如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B北偏西35°方向,则∠ABC的度数为°.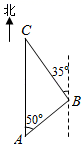 13. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .14. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm.
13. 在平行四边形ABCD中,∠A=30°,AD= ,BD=4,则平行四边形ABCD的面积等于 .14. 如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为cm. 15. 如图,若AB∥CD,∠1=40度,则∠2=度.
15. 如图,若AB∥CD,∠1=40度,则∠2=度.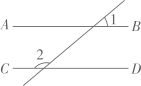 16. 已知四边形 是矩形,点E是矩形 的边上的点,且 .若 , ,则 的长是.17. 已知 的三个顶点都是同一个正方形的顶点, 的平分线与线段 交于点D . 若 的一条边长为6,则点D到直线 的距离为 .
16. 已知四边形 是矩形,点E是矩形 的边上的点,且 .若 , ,则 的长是.17. 已知 的三个顶点都是同一个正方形的顶点, 的平分线与线段 交于点D . 若 的一条边长为6,则点D到直线 的距离为 .
三、解答题
-
18. 如图,AC是∠BAE的平分线,点D是线段AC上的一点,∠C=∠E,AB=AD.求证:BC=DE.
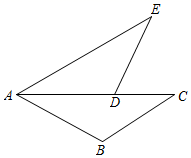 19. 如图,已知 , .求证: .
19. 如图,已知 , .求证: . 20. 已知:如图,AB=AD,BC=DC.求证:∠B=∠D.
20. 已知:如图,AB=AD,BC=DC.求证:∠B=∠D.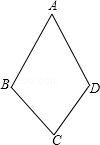 21. 如图,在四边形 中, 与 相交于点E . 求证: .
21. 如图,在四边形 中, 与 相交于点E . 求证: .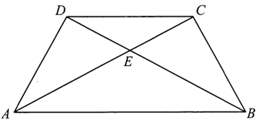
四、作图题
-
22. 如图,点P是⊙O的直径AB延长线上的一点(PB<OB),点E是线段OP的中点.
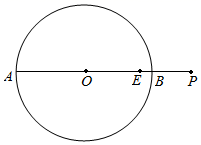 (1)、尺规作图:在直径AB上方的圆上作一点C,使得EC=EP,连接EC,PC(保留清晰作图痕迹,不要求写作法);并证明PC是⊙O的切线;(2)、在(1)的条件下,若BP=4,EB=1,求PC的长.
(1)、尺规作图:在直径AB上方的圆上作一点C,使得EC=EP,连接EC,PC(保留清晰作图痕迹,不要求写作法);并证明PC是⊙O的切线;(2)、在(1)的条件下,若BP=4,EB=1,求PC的长.五、综合题
-
23. 如图,四边形 是菱形,点H为对角线 的中点,点E在 的延长线上, ,垂足为E,点F在 的延长线上, ,垂足为F.
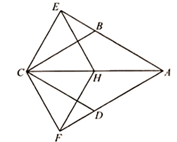 (1)、若 ,求证:四边形 是菱形;(2)、若 , 的面积为16,求菱形 的面积.24. 如图, 为⊙O的直径, 为⊙O上一点, ,垂足为D, 平分 .
(1)、若 ,求证:四边形 是菱形;(2)、若 , 的面积为16,求菱形 的面积.24. 如图, 为⊙O的直径, 为⊙O上一点, ,垂足为D, 平分 .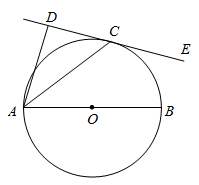 (1)、求证: 是⊙O的切线;(2)、若 , ,求 的长.25. 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)、求证: 是⊙O的切线;(2)、若 , ,求 的长.25. 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.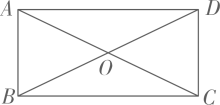 (1)、求证:四边形ABCD是矩形;(2)、若∠AOB∶∠ODC=4∶3,求∠ADO的度数.26. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .
(1)、求证:四边形ABCD是矩形;(2)、若∠AOB∶∠ODC=4∶3,求∠ADO的度数.26. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .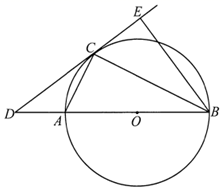 (1)、求证: 是 的切线:(2)、若 ,求 的长.27. 如图,四边形 是矩形,E、F分别是线段 、 上的点,点O是 与 的交点.若将 沿直线 折叠,则点E与点F重合.
(1)、求证: 是 的切线:(2)、若 ,求 的长.27. 如图,四边形 是矩形,E、F分别是线段 、 上的点,点O是 与 的交点.若将 沿直线 折叠,则点E与点F重合. (1)、求证:四边形 是菱形;(2)、若 ,求 的值.28. 如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点.
(1)、求证:四边形 是菱形;(2)、若 ,求 的值.28. 如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点. (1)、求证:四边形AEFD是矩形;(2)、如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF上时,则有OB=OM.请说明理由;(3)、如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,DM,当△AMD是等腰三角形时,求AP的长.29. 如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED= .
(1)、求证:四边形AEFD是矩形;(2)、如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,当点M落在线段EF上时,则有OB=OM.请说明理由;(3)、如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,DM,当△AMD是等腰三角形时,求AP的长.29. 如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED= .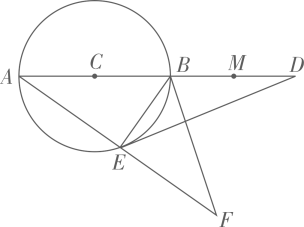 (1)、求证:△DEB∽△DAE;(2)、求DA,DE的长;(3)、若点F在B、E、M三点确定的圆上,求MD的长.
(1)、求证:△DEB∽△DAE;(2)、求DA,DE的长;(3)、若点F在B、E、M三点确定的圆上,求MD的长.
-