云南省中考数学真题汇编（近几年）3 函数

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，在平面直角坐标系中，将△OAB（顶点为网格线交点）绕原点O顺时针旋转90°，得到△OA′B′，若反比例函数y= $\frac{k}{x}$ 的图象经过点A的对应点A′，则k的值为（）

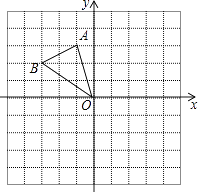A、-6 B、﹣3 C、3 D、6

查看试题解析
2. 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与y轴交于点B（0，﹣2），点A（﹣1，m）在抛物线上，则下列结论中错误的是（）

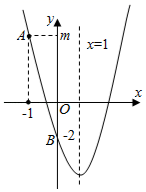A、ab＜0 B、一元二次方程ax²+bx+c＝0的正实数根在2和3之间 C、a＝ $\frac{m + 2}{3}$ D、点P₁（t，y₁），P₂（t+1，y₂）在抛物线上，当实数t＞ $\frac{1}{3}$ 时，y₁＜y₂

查看试题解析
3. 如图，点A在双曲线y═ $\frac{k}{x}$ （x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于 $\frac{1}{2}$ OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F（0，2），连接AC．若AC=1，则k的值为（）

A、2 B、 $\frac{32}{25}$ C、 $\frac{4 \sqrt{3}}{5}$ D、 $\frac{2 \sqrt{5} + 2}{5}$

查看试题解析

二、填空题

4. 已知一个反比例函数的图象经过点 $(3 ， 1)$ ，若该反比例函数的图象也经过点 $(- 1 ， m)$ ，则 $m =$ .

查看试题解析
5. 若点(3，5)在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则k＝.

查看试题解析
6. 已知点P（a，b）在反比例函数y= $\frac{2}{x}$ 的图象上，则ab= ．

查看试题解析
7. 若反比例函数的图象经过点 $(1 ， - 2)$ ，则该反比例函数的解析式（解析式也称表达式）为．

查看试题解析
8. 如图，点A的坐标为（4，2）．将点A绕坐标原点O旋转90°后，再向左平移1个单位长度得到点A′，则过点A′的正比例函数的解析式为．

查看试题解析
9. 已知点A（a，b）在双曲线y= $\frac{5}{x}$ 上，若a、b都是正整数，则图象经过B（a，0）、C（0，b）两点的一次函数的解析式（也称关系式）为．

查看试题解析

三、综合题

10. 某鲜花销售公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成．

如图中的射线 $l_{1}$ ，射线 $l_{2}$ 分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资 $y_{1}$ （单位：元）和 $y_{2}$ （单位：元）与其当月鲜花销售量x（单位：千克）（ $x \geq 0$ ）的函数关系．

(1)、分别求 $y_{1}$ ﹑ $y_{2}$ 与x的函数解析式（解析式也称表达式）；

(2)、若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过2000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？

查看试题解析
11. 为了做好校园疫情防控工作，校医每天早上对全校办公室和教室进行药物喷洒消毒，她完成3间办公室和2间教室的药物喷洒要19min；完成2间办公室和1间教室的药物喷洒要11min.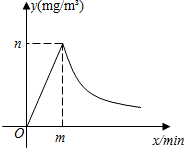

(1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间？

(2)、消毒药物在一间教室内空气中的浓度y（单位：mg/m³）与时间x（单位：min）的函数关系如图所示：校医进行药物喷洒时y与x的函数关系式为y＝2x，药物喷洒完成后y与x成反比例函数关系，两个函数图象的交点为A（m，n）.当教室空气中的药物浓度不高于1mg/m³时，对人体健康无危害，校医依次对一班至十一班教室（共11间）进行药物喷洒消毒，当她把最后一间教室药物喷洒完成后，一班学生能否进入教室？请通过计算说明.

查看试题解析
12. 如图，两条抛物线 $y_{1} = - x^{2} + 4$ ， $y_{2} = - \frac{1}{5} x^{2} + b x + c$ 相交于A，B两点，点A在x轴负半轴上，且为抛物线 $y_{2}$ 的最高点.

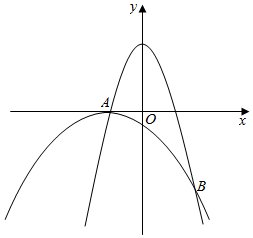(1)、求抛物线 $y_{2}$ 的解析式和点B的坐标；

(2)、点C是抛物线 $y_{1}$ 上A，B之间的一点，过点C作x轴的垂线交 $y_{2}$ 于点D，当线段CD取最大值时，求 $S_{△ B C D}$ .

查看试题解析
13. 众志成城抗疫情，全国人民在行动.某公司决定安排大、小货车共20辆，运送260吨物资到A地和B地，支援当地抗击疫情.每辆大货车装15吨物资，每辆小货车装10吨物资，这20辆货车恰好装完这批物资.已知这两种货车的运费如下表：

A地（元/辆）

B地（元/辆）

大货车

900

1000

小货车

500

700

现安排上述装好物资的20辆货车（每辆大货车装15吨物资，每辆小货车装10吨物资）中的10辆前往A地，其余前往B地，设前往A地的大货车有x辆，这20辆货车的总运费为y元.

(1)、这20辆货车中，大货车、小货车各有多少辆？

(2)、求 $y$ 与 $x$ 的函数解析式，并直接写出 $x$ 的取值范围；

(3)、若运往A地的物资不少于140吨，求总运费y的最小值.

查看试题解析
14. 已知k是常数，抛物线y＝x²＋(k²＋k－6)x＋3k的对称轴是y轴，并且与x轴有两个交点.

(1)、求k的值：

(2)、若点P在抛物线y＝x²＋(k²＋k－6)x＋3k上，且P到y轴的距离是2，求点P的坐标.

查看试题解析
15. 某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克，规定销售单价不低于成本，又不高于成本的两倍.经过市场调查发现，某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示：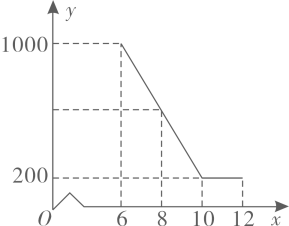

(1)、求y与x的函数解析式(也称关系式)；

(2)、求这一天销售西瓜获得的利润的最大值.

查看试题解析
16. 某公司计划购买A，B两种型号的电脑，已知购买一台A型电脑需0.6万元，购买一台B型电脑需0.4万元，该公司准备投入资金y万元，全部用于购进35台这两种型号的电脑，设购进A型电脑x台．

(1)、求y关于x的函数解析式；

(2)、若购进B型电脑的数量不超过A型电脑数量的2倍，则该公司至少需要投入资金多少万元？

查看试题解析
17. 如图，抛物线y=ax²+bx过点B（1，﹣3），对称轴是直线x=2，且抛物线与x轴的正半轴交于点A．

(1)、求抛物线的解析式，并根据图象直接写出当y≤0时，自变量x的取值范围；

(2)、在第二象限内的抛物线上有一点P，当PA⊥BA时，求△PAB的面积．

查看试题解析
18. 已知二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象经过A（0，3），B（﹣4，﹣ $\frac{9}{2}$ ）两点．

(1)、求b，c的值．

(2)、二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象与x轴是否有公共点，求公共点的坐标；若没有，请说明情况．

查看试题解析
19. 某驻村扶贫小组为解决当地贫困问题，带领大家致富．经过调查研究，他们决定利用当地生产的甲乙两种原料开发A，B两种商品，为科学决策，他们试生产A、B两种商品100千克进行深入研究，已知现有甲种原料293千克，乙种原料314千克，生产1千克A商品，1千克B商品所需要的甲、乙两种原料及生产成本如下表所示．

甲种原料（单位：千克）
乙种原料（单位：千克）
生产成本（单位：元）
A商品
3
2
120
B商品
2.5
3.5
200
设生产A种商品x千克，生产A、B两种商品共100千克的总成本为y元，根据上述信息，解答下列问题：

(1)、求y与x的函数解析式（也称关系式），并直接写出x的取值范围；

(2)、x取何值时，总成本y最小？

查看试题解析
20. 已知抛物线 $y = - 2 x^{2} + b x + c$ 经过点 $(0 ， - 2)$ ，当 $x < - 4$ 时，y随x的增大而增大，当 $x > - 4$ 时，y随x的增大而减小．设r是抛物线 $y = - 2 x^{2} + b x + c$ 与x轴的交点（交点也称公共点）的横坐标， $m = \frac{r^{9} + r^{7} - 2 r^{5} + r^{3} + r - 1}{r^{9} + 60 r^{5} - 1}$ ．

(1)、求b、c的值：

(2)、求证： $r^{4} - 2 r^{2} + 1 = 60 r^{2}$ ；

(3)、以下结论： $m < 1 ， m = 1 ， m > 1$ ，你认为哪个符合题意？请证明你认为正确的那个结论．

查看试题解析
21. 抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于A、B两点，与y轴交于点C，点A的坐标为 $(- 1 ， 0)$ ，点C的坐标为 $(0 ， - 3)$ .点P为抛物线 $y = x^{2} + b x + c$ 上的一个动点.过点P作 $P D ⊥ x$ 轴于点D，交直线 $B C$ 于点E.

(1)、求b、c的值；

(2)、设点 $F$ 在抛物线 $y = x^{2} + b x + c$ 的对称轴上，当 $△ A C F$ 的周长最小时，直接写出点F的坐标；

(3)、在第一象限，是否存在点P，使点P到直线 $B C$ 的距离是点D到直线 $B C$ 的距离的5倍？若存在，求出点P所有的坐标；若不存在，请说明理由.

查看试题解析
22. 如图：在平面直角坐标系中，直线l：y= $\frac{1}{3}$ x﹣ $\frac{4}{3}$ 与x轴交于点A，经过点A的抛物线y=ax²﹣3x+c的对称轴是x= 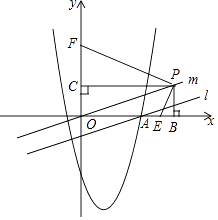$\frac{3}{2}$ ．

(1)、求抛物线的解析式；

(2)、平移直线l经过原点O，得到直线m，点P是直线m上任意一点，PB⊥x轴于点B，PC⊥y轴于点C，若点E在线段OB上，点F在线段OC的延长线上，连接PE，PF，且PF=3PE．求证：PE⊥PF；

(3)、若（2）中的点P坐标为（6，2），点E是x轴上的点，点F是y轴上的点，当PE⊥PF时，抛物线上是否存在点Q，使四边形PEQF是矩形？如果存在，请求出点Q的坐标，如果不存在，请说明理由．

查看试题解析

	A地（元/辆）	B地（元/辆）
大货车	900	1000
小货车	500	700

	甲种原料（单位：千克）	乙种原料（单位：千克）	生产成本（单位：元）
A商品	3	2	120
B商品	2.5	3.5	200