云南省中考数学真题汇编（近几年）1 数与式

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 ${(\frac{1}{2})}^{- 1} = - 2$ C、 ${(- 3 a)}^{3} = - 9 a^{3}$ D、 $a^{6} \div a^{3} = a^{3} (a \neq 0)$

查看试题解析
2. 某地区2021年元旦的最高气温为 $9 ℃$ ，最低气温为 $- 2 ℃$ ，那么该地区这天的最低气温比最高气温低（）

A、 $7 ℃$ B、 $- 7 ℃$ C、 $11 ℃$ D、 $- 11 ℃$

查看试题解析
3. 某款国产手机上有科学计算器，依次按键： $4 \sin (60) =$ ，显示的结果在哪两个相邻整数之间（）

A、2～3 B、3～4 C、4～5 D、5～6

查看试题解析
4. 千百年来的绝对贫困即将消除，云南省 $95 %$ 的贫困人口脱贫， $95 %$ 的贫困村出列， $90 %$ 的贫困县摘帽，1500000人通过易地扶贫搬迁实现“挪穷窝”，“斩穷根”（摘自2020年5月11日云南日报）.1500000这个数用科学记数法表示为（）

A、 $15 \times 10^{6}$ B、 $1.5 \times 10^{5}$ C、 $1.5 \times 10^{6}$ D、 $1.5 \times 10^{7}$

查看试题解析
5. 要使 $\frac{\sqrt{x + 1}}{2}$ 有意义，则x的取值范围为（）

A、x≤0 B、x≥－1 C、x≥0 D、x≤－1

查看试题解析
6. 2019年“五一”期间，某景点接待海内外游客共688000人次，688000这个数用科学记数法表示为（）

A、68.8×10⁴ B、0.688×10⁶ C、6.88×10⁵ D、6.88×10⁶

查看试题解析
7. 按一定规律排列的单项式： $a^{2} ， 4 a^{3} ， 9 a^{4} ， 16 a^{5} ， 25 a^{6}$ ，……，第n个单项式是（）

A、 $n^{2} a^{n + 1}$ B、 $n^{2} a^{n - 1}$ C、 $n^{n} a^{n + 1}$ D、 ${(n + 1)}^{2} a^{n}$

查看试题解析
8. 下列运算中，正确的是（）

A、 $\sqrt{5}$ ﹣2 $\sqrt{5}$ ＝﹣2 B、6a⁴b÷2a³b＝3ab C、（﹣2a²b）³＝﹣8a⁶b³ D、 $\frac{a}{a - 1} \cdot \frac{a^{2} - 2 a + 1}{1 - a} = a$

查看试题解析
9. 按一定规律排列的单项式：a， $- 2 a$ ， $4 a$ ， $- 8 a$ ， $16 a$ ， $- 32 a$ ，…，第n个单项式是（）

A、 ${(- 2)}^{n - 1} a$ B、 ${(- 2)}^{n} a$ C、 $2^{n - 1} a$ D、 $2^{n} a$

查看试题解析
10. 截止2018年5月末，中国人民银行公布的数据显示，我国外汇的储备规模约为3.11×10⁴亿元美元，则3.11×10⁴亿表示的原数为（）

A、2311000亿 B、31100亿 C、3110亿 D、311亿

查看试题解析
11. 下列计算正确的是（）

A、a²•a=a² B、a⁶÷a²=a³ C、a²b﹣2ba²=﹣a²b D、（﹣ $\frac{3}{2 a}$ ）³=﹣ $\frac{9}{8 a^{3}}$

查看试题解析
12. 按一定规律排列的单项式：x³ ，－x⁵ ， x⁷ ，－x⁹ ， x¹¹ ， ……第n个单项式是（）

A、(－1)ⁿ^－¹x²ⁿ^－¹ B、(－1)ⁿx²ⁿ^－¹ C、(－1)ⁿ^－¹x²ⁿ^＋¹ D、(－1)ⁿx²ⁿ^＋¹

查看试题解析

二、填空题

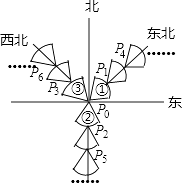
13. 要使 $\frac{5}{x + 1}$ 有意义，则x的取值范围是.

查看试题解析
14. 若零上8℃记作＋8℃，则零下6℃记作℃..

查看试题解析
15. 中国是最早采用正负数表示相反意义的量的国家.某仓库运进面粉7吨，记为 $+ 7$ 吨，那么运出面粉8吨应记为吨.

查看试题解析
16. 分解因式：x²-2x+1=.

查看试题解析
17. 观察下列一组数：﹣ $\frac{2}{3}$ ， $\frac{6}{9}$ ，﹣ $\frac{12}{27}$ ， $\frac{20}{81}$ ，﹣ $\frac{30}{243}$ ，…，它们是按一定规律排列的，那么这一组数的第n个数是.

查看试题解析
18. 若m+ $\frac{1}{m}$ =3，则m²+ $\frac{1}{m^{2}}$ = ．

查看试题解析
19. 如图：图象①②③均是以P₀为圆心，1个单位长度为半径的扇形，将图形①②③分别沿东北，正南，西北方向同时平移，每次移动一个单位长度，第一次移动后图形①②③的圆心依次为P₁P₂P₃ ，第二次移动后图形①②③的圆心依次为P₄P₅P₆…，依此规律，P₀P₂₀₁₈=个单位长度．

查看试题解析

三、计算题

20. 计算： ${(- 3)}^{2} + \frac{\tan 45 °}{2} + {(\sqrt{2} - 1)}^{0} - 2^{- 1} + \frac{2}{3} \times (- 6)$ ．

查看试题解析
21. 计算：1²⁰²¹﹣ $\sqrt[3]{8}$ +（π﹣3.14）⁰﹣（﹣ $\frac{1}{5}$ ）^-1.

查看试题解析
22. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x^{2} - 4} \div \frac{x^{2} - 2 x}{x + 2}$ ，其中 $x = \frac{1}{2}$ .

查看试题解析
23. 计算： $3^{2} - {(π - 5)}^{0} - \sqrt{4} + {(- 1)}^{- 2}$ .

查看试题解析
24. 先化简，再求值（ $\frac{1}{a - b}$ ﹣ $\frac{b}{a^{2} - b^{2}}$ ）÷ $\frac{a^{2} - a b}{a^{2} - 2 a b + b^{2}}$ ，其中a，b满足a+b﹣ $\frac{1}{2}$ =0．

查看试题解析
25. 计算﹣（﹣2）+（π﹣3.14）⁰+ $\sqrt[3]{27}$ +（﹣ $\frac{1}{3}$ ）^﹣¹

查看试题解析
26. 先化简，再求值：（ $\frac{1}{a - 2}$ +1）÷ $\frac{a^{2} - 1}{3 a - 6}$ ，其中a=tan60°﹣|﹣1|．

查看试题解析
27. 计算： $\sqrt{18}$ ﹣2cos45°﹣（ $\frac{1}{3}$ ）^﹣¹﹣（π﹣1）⁰

查看试题解析

四、综合题

28. 已知抛物线 $y = - 2 x^{2} + b x + c$ 经过点 $(0 ， - 2)$ ，当 $x < - 4$ 时，y随x的增大而增大，当 $x > - 4$ 时，y随x的增大而减小．设r是抛物线 $y = - 2 x^{2} + b x + c$ 与x轴的交点（交点也称公共点）的横坐标， $m = \frac{r^{9} + r^{7} - 2 r^{5} + r^{3} + r - 1}{r^{9} + 60 r^{5} - 1}$ ．

(1)、求b、c的值：

(2)、求证： $r^{4} - 2 r^{2} + 1 = 60 r^{2}$ ；

(3)、以下结论： $m < 1 ， m = 1 ， m > 1$ ，你认为哪个符合题意？请证明你认为正确的那个结论．

查看试题解析
29. 观察下列各个等式的规律：
第一个等式： $\frac{2^{2} - 1^{2} - 1}{2}$ =1，第二个等式： $\frac{3^{2} - 2^{2} - 1}{2}$ =2，第三个等式： $\frac{4^{2} - 3^{2} - 1}{2}$ =3…
请用上述等式反映出的规律解决下列问题：

(1)、直接写出第四个等式；

(2)、猜想第n个等式（用n的代数式表示），并证明你猜想的等式是正确的．

查看试题解析
30. 有一列按一定顺序和规律排列的数：
第一个数是 $\frac{1}{1 \times 2}$ ；
第二个数是 $\frac{1}{2 \times 3}$ ；
第三个数是 $\frac{1}{3 \times 4}$ ；
…
对任何正整数n，第n个数与第（n+1）个数的和等于 $\frac{2}{n \times (n + 2)}$ ．

(1)、经过探究，我们发现： $\frac{1}{1 \times 2} = \frac{1}{1} - \frac{1}{2} \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$
设这列数的第5个数为a，那么 $a > \frac{1}{5} - \frac{1}{6}$ ， $a = \frac{1}{5} - \frac{1}{6}$ ， $a < \frac{1}{5} - \frac{1}{6}$ ，哪个正确？
请你直接写出正确的结论；

(2)、请你观察第1个数、第2个数、第3个数，猜想这列数的第n个数（即用正整数n表示第n数），并且证明你的猜想满足“第n个数与第（n+1）个数的和等于 $\frac{2}{n \times (n + 2)}$ ”；

(3)、设M表示 $\frac{1}{1^{2}}$ ， $\frac{1}{2^{2}}$ ， $\frac{1}{3^{2}}$ ，…， $\frac{1}{2016^{2}}$ ，这2016个数的和，即 $M = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \dots \dots + \frac{1}{2016^{2}}$ ，
求证： $\frac{2016}{2017} < M < \frac{4031}{2016}$ ．

查看试题解析