上海市中考数学真题汇编(近几年)5 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )A、平行四边形 B、等腰梯形 C、正六边形 D、圆
二、填空题
-
2. 如图,已知 ,则 .
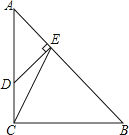
 3. 在矩形ABCD中,AB=6,BC=8,点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是 .4. 如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是 .5. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD , 从木杆的顶端D观察井水水岸C , 视线DC与井口的直径AB交于点E , 如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为米.
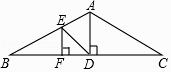
3. 在矩形ABCD中,AB=6,BC=8,点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是 .4. 如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是 .5. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD , 从木杆的顶端D观察井水水岸C , 视线DC与井口的直径AB交于点E , 如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为米. 6. 如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,联结AD . 如果将△ACD沿直线AD翻折后,点C的对应点为点E , 那么点E到直线BD的距离为 .
6. 如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,联结AD . 如果将△ACD沿直线AD翻折后,点C的对应点为点E , 那么点E到直线BD的距离为 . 7. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.8. 如图,在正方形ABCD中,E是边AD的中点.将△ABE沿直线BE翻折,点A落在点F处,联结DF,那么∠EDF的正切值是.
7. 在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且 ,那么AD的长是.8. 如图,在正方形ABCD中,E是边AD的中点.将△ABE沿直线BE翻折,点A落在点F处,联结DF,那么∠EDF的正切值是.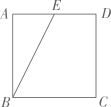 9. 如图,已知平行四边形ABCD,E是边BC的中点,联结DE并延长,与AB的延长线交于点F.设 = , = 那么向量 用向量 、 表示为 .
9. 如图,已知平行四边形ABCD,E是边BC的中点,联结DE并延长,与AB的延长线交于点F.设 = , = 那么向量 用向量 、 表示为 .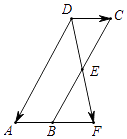 10. 如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 .
10. 如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 .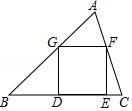 11.
11.如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为 .

三、综合题
-
12. 已知在 中, , , 为 边上的中线.
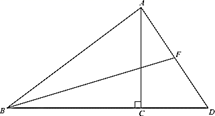 (1)、求 的长;(2)、求 的值.13. 如图,在梯形 中, 是对角线 的中点,联结 并延长交边 或边 于E.
(1)、求 的长;(2)、求 的值.13. 如图,在梯形 中, 是对角线 的中点,联结 并延长交边 或边 于E. (1)、当点E在边 上时,
(1)、当点E在边 上时,①求证: ;
②若 ,求 的值;
(2)、若 ,求 的长.14.已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
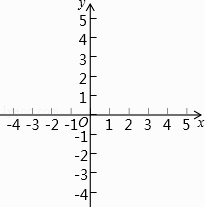 (1)、求这条抛物线的表达式和点B的坐标;(2)、点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;(3)、将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
(1)、求这条抛物线的表达式和点B的坐标;(2)、点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;(3)、将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
-