上海市中考数学真题汇编（近几年）4 图形的性质
试卷更新日期：2021-08-20 类型：二轮复习
一、单选题
-
1. 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（ ）A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC2. 下列命题中，真命题是（ ）A、对角线互相垂直的梯形是等腰梯形 B、对角线互相垂直的平行四边形是正方形 C、对角线平分一组对角的平行四边形是菱形 D、对角线平分一组对角的梯形是直角梯形3. 如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是（ ）A、平行四边形 B、等腰梯形 C、正六边形 D、圆4. 下列命题中，假命题是( )A、矩形的对角线相等 B、矩形对角线交点到四个顶点的距离相等 C、矩形的对角线互相平分 D、矩形对角线交点到四条边的距离相等5. 已知⊙A与⊙B外切，⊙C与⊙A、⊙B都内切，且AB＝5，AC＝6，BC＝7，那么⊙C的半径长是（ ）A、11 B、10 C、9 D、86. 如图，已知∠POQ=30°，点A，B在射线OQ上（点A在点O、B之间），半径长为2的⊙A与直线OP相切，半径长为3的⊙B与⊙A相交，那么OB的取值范围是（ ）
A、5＜OB＜9 B、4＜OB＜9 C、3＜OB＜7 D、2＜OB＜77. 如图，已知平行四边形ABCD中， ，E为 中点，求 （ ）
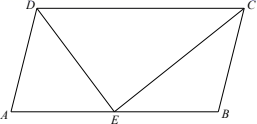A、 B、 C、 D、8. 如图，已知长方形 中， ，圆B的半径为1，圆A与圆B内切，则点 与圆A的位置关系是（ ）
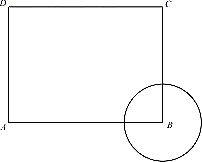A、点C在圆A外，点D在圆A内 B、点C在圆A外，点D在圆A外 C、点C在圆A上，点D在圆A内 D、点C在圆A内，点D在圆A外二、填空题
-
9. 的余角是 ．10. 在矩形ABCD中，AB=6，BC=8，点O在对角线AC上，圆O的半径为2，如果圆O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是 ．11. 如图，AC、BD是平行四边形ABCD的对角线，设 = ， = ，那么向量 用向量 表示为 ．
12. 六个带 角的直角三角板拼成一个正六边形，直角三角板的最短边为1，求中间正六边形的面积 ．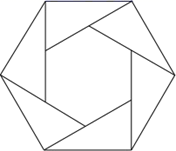
13. 如图，在△ABC中，AB=4，BC=7，∠B=60°，点D在边BC上，CD=3，联结AD ． 如果将△ACD沿直线AD翻折后，点C的对应点为点E ， 那么点E到直线BD的距离为 ．
14. 如图，已知直线l1∥l2 ， 含30°角的三角板的直角顶点C在l1上，30°角的顶点A在l2上，如果边AB与l1的交点D是AB的中点，那么∠1＝度.
15. 如图，在正边形ABCDEF中，设 ， ，那么向量 用向量 表示为.
16. 在△ABC和△A1B1C1中，已知∠C＝∠C1＝90°，AC＝A1C1＝3，BC＝4，B1C1＝2，点D、D1分别在边AB、A1B1上，且 ，那么AD的长是.17. 如图，在正方形ABCD中，E是边AD的中点.将△ABE沿直线BE翻折，点A落在点F处，联结DF，那么∠EDF的正切值是.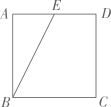
18. 如图，已知平行四边形ABCD，E是边BC的中点，联结DE并延长，与AB的延长线交于点F．设 = ， = 那么向量 用向量 、 表示为 ．
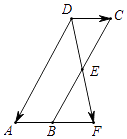19. 通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题．如果从某个多边形的一个顶点出发的对角线共有2条，那么该多边形的内角和是度．20. 对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点（如图1），那么这个矩形水平方向的边长称为该图形的宽，铅锤方向的边长称为该矩形的高．如图2，菱形ABCD的边长为1，边AB水平放置．如果该菱形的高是宽的 ，那么它的宽的值是 ．
21. 定义：在平面内，一个点到图形的距离是这个点到这个图上所有点的最短距离，在平面内有一个正方形，边长为2，中心为O，在正方形外有一点 ，当正方形绕着点O旋转时，则点P到正方形的最短距离d的取值范围为 ．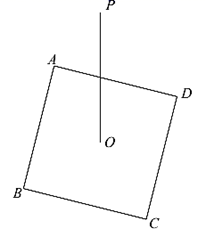
三、综合题
-
22. 已知在 中， ， ， 为 边上的中线．
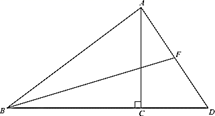(1)、求 的长；(2)、求 的值．23. 如图，△ABC中，AB=AC ， ⊙O是△ABC的外接圆，BO的延长交边AC于点D ．
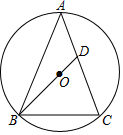(1)、求证：∠BAC=2∠ABD；(2)、当△BCD是等腰三角形时，求∠BCD的大小；(3)、当AD=2，CD=3时，求边BC的长．24. 如图，在直角梯形ABCD中， ，∠DAB=90°，AB=8，CD=5，BC=3 ．
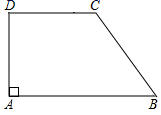(1)、求梯形ABCD的面积；(2)、联结BD ， 求∠DBC的正切值．25. 已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF ， CE的延长线交DA的延长线于点G ， CF的延长线交BA的延长线于点H ．
(1)、求证：△BEC∽△BCH；(2)、如果BE2=AB•AE ， 求证：AG=DF ．26. 如图1是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角为60°时，箱盖ADE落在AD'E'的位置（如图2所示）.已知AD＝90厘米，DE＝30厘米，EC＝40厘米.
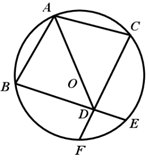
(1)、求点D'到BC的距离；(2)、求E、E'两点的距离.27. 如图1，AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线，过点A作AE⊥AD，交BD的延长线于点E.
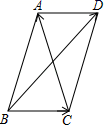
(1)、求证：∠E＝ ∠C；(2)、如图2，如果AE＝AB，且BD：DE＝2：3，求cos∠ABC的值；(3)、如果∠ABC是锐角，且△ABC与△ADE相似，求∠ABC的度数，并直接写出 的值.28. 已知：在圆O内，弦 与弦 交于点 分别是 和 的中点，联结 ．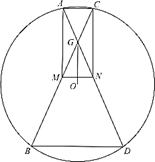
(1)、求证： ；(2)、联结 ，当 时，求证：四边形 为矩形．29. 如图，已知△ABC中，AB=BC=5，tan∠ABC= ．
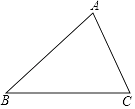(1)、求边AC的长；(2)、设边BC的垂直平分线与边AB的交点为D，求 的值．
30. 已知⊙O的直径AB=2，弦AC与弦BD交于点E．且OD⊥AC，垂足为点F．
(1)、如图1，如果AC=BD，求弦AC的长；
(2)、如图2，如果E为弦BD的中点，求∠ABD的余切值；(3)、联结BC、CD、DA，如果BC是⊙O的内接正n边形的一边，CD是⊙O的内接正（n+4）边形的一边，求△ACD的面积．31. 已知：如图，正方形ABCD中，P是边BC上一点，BE⊥AP，DF⊥AP，垂足分别是点E、F．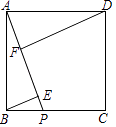
(1)、求证：EF=AE﹣BE；
(2)、联结BF，如课 = ．求证：EF=EP．
