上海市中考数学真题汇编（近几年）3 函数

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 将抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 向下平移两个单位，以下说法错误的是（）

A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变

查看试题解析
2. 已知反比例函数的图象经过点(2，﹣4)，那么这个反比例函数的解析式是（）

A、y= $\frac{2}{x}$ B、y=﹣ $\frac{2}{x}$ C、y= $\frac{8}{x}$ D、y=﹣ $\frac{8}{x}$

查看试题解析
3. 下列函数中，函数值y随自变量x的值增大而增大的是( )

A、 $y = \frac{x}{3}$ B、 $y = - \frac{x}{3}$ C、 $y = \frac{3}{x}$ D、 $y = - \frac{3}{x}$

查看试题解析
4. 下列对二次函数y=x²﹣x的图象的描述，正确的是（）

A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧部分是下降的

查看试题解析
5. 如果一次函数y=kx+b（k、b是常数，k≠0）的图象经过第一、二、四象限，那么k、b应满足的条件是（）

A、k＞0，且b＞0 B、k＜0，且b＞0 C、k＞0，且b＜0 D、k＜0，且b＜0

查看试题解析

二、填空题

6. 如果一次函数y=kx+3（k是常数，k≠0）的图象经过点（1，0），那么y的值随x的增大而．（填“增大”或“减小”）

查看试题解析
7. 已知函数 $y = k x$ 经过二、四象限，且函数不经过 $(- 1 ， 1)$ ，请写出一个符合条件的函数解析式．

查看试题解析
8. 如果函数y＝kx（k≠0）的图象经过第二、四象限，那么y的值随x的值增大而．（填“增大”或“减小”）

查看试题解析
9. 如果将抛物线y=x²向上平移3个单位，那么所得新抛物线的表达式是．

查看试题解析
10. 小明从家步行到学校需走的路程为1800米．图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行米．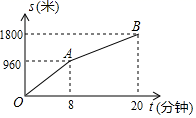

查看试题解析
11. 在登山过程中，海拔每升高1千米，气温下降6℃，已知某登山大本营所在的位置的气温是2℃，登山队员从大本营出发登山，当海拔升高x千米时，所在位置的气温是y℃，那么y关于x的函数解析式是.

查看试题解析
12. 已知f(x)＝x²－1，那么f(－1)＝.

查看试题解析
13. 已知反比例函数y= $\frac{k - 1}{x}$ （k是常数，k≠1）的图象有一支在第二象限，那么k的取值范围是．

查看试题解析
14. 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量与售价之间的关系如图所示，成本为5元/千克，现以8元/千克卖出，赚元．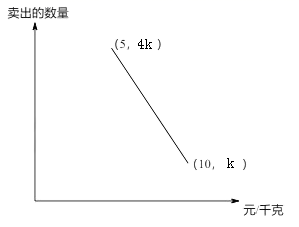

查看试题解析

三、综合题

15. 在平面直角坐标系xOy中，直线y=﹣ $\frac{1}{2}$ x+5与x轴、y轴分别交于点A、B(如图)．抛物线y=ax²+bx(a≠0)经过点A ．

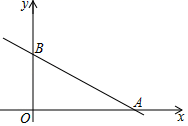(1)、求线段AB的长；

(2)、如果抛物线y=ax²+bx经过线段AB上的另一点C ，且BC= $\sqrt{5}$ ，求这条抛物线的表达式；

(3)、如果抛物线y=ax²+bx的顶点D位于△AOB内，求a的取值范围．

查看试题解析
16. 在平面直角坐标系xOy中(如图)，已知抛物线y＝x²－2x ，其顶点为A.

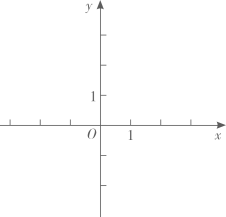(1)、写出这条抛物线的开口方向、顶点A的坐标，并说明它的变化情况；

(2)、我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”
①试求抛物线y＝x²－2x的“不动点”的坐标；

②平移抛物线y＝x²－2x ，使所得新抛物线的顶点B是该抛物线的“不动点”，其对称轴与x轴交于点C，且四边形OABC是梯形，求新抛物线的表达式.

查看试题解析
17. 在平面直角坐标系xOy中（如图），已知一次函数的图象平行于直线 $y = \frac{1}{2} x$ ，且经过点A（2，3），与x轴交于点B。

(1)、求这个一次函数的解析式；

(2)、设点C在y轴上，当AC＝BC时，求点C的坐标。

查看试题解析
18. 一辆汽车在某次行驶过程中，油箱中的剩余油量y（升）与行驶路程x（千米）之间是一次函数关系，其部分图象如图所示．

(1)、求y关于x的函数关系式；（不需要写定义域）

(2)、已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？

查看试题解析
19. 在平面直角坐标系xOy中（如图）．已知抛物线y=﹣ $\frac{1}{2}$ x²+bx+c经过点A（﹣1，0）和点B（0， $\frac{5}{2}$ ），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．

(1)、求这条抛物线的表达式；

(2)、求线段CD的长；

(3)、将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．

查看试题解析
20. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．
甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示．
乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．

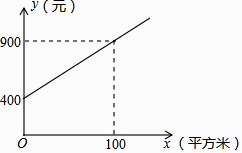(1)、求如图所示的y与x的函数解析式：（不要求写出定义域）；

(2)、如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．

查看试题解析
21.
已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x²+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．

(1)、求这条抛物线的表达式和点B的坐标；

(2)、点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；

(3)、将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．

查看试题解析
22. 已知抛物线 $y = a x^{2} + c (a \neq 0)$ 过点 $P (3 ， 0) ， Q (1 ， 4)$ ．

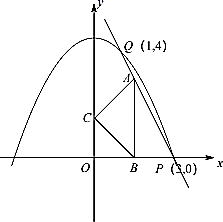(1)、求抛物线的解析式；

(2)、点A在直线 $P Q$ 上且在第一象限内，过A作 $A B ⊥ x$ 轴于B，以 $A B$ 为斜边在其左侧作等腰直角 $A B C$ ．
①若A与Q重合，求C到抛物线对称轴的距离；

②若C落在抛物线上，求C的坐标．

查看试题解析