山西省中考数学真题汇编（近几年） 6 统计与概率
试卷更新日期：2021-08-20 类型：二轮复习
一、单选题
-
1. 在体育课上，甲、乙两名同学分别进行了5次跳远测试，经计算他们的平均成绩相同．若要比较这两名同学的成绩哪一个更为稳定，通常需要比较他们成绩的（ ）A、众数 B、平均数 C、中位数 D、方差2. 近年来快递业发展迅速，下表是2018年1～3月份我省部分地市邮政快递业务量的统计结果（单位：万件）：
太原市
大同市
长治市
晋中市
运城市
临汾市
吕梁市
3303.78
332.68
302.34
319.79
725.86
416.01
338.87
1～3月份我省这七个地市邮政快递业务量的中位数是（ ）
A、319.79万件 B、332.68万件 C、338.87万件 D、416.01万件3. 在一个不透明的袋子里装有两个黄球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，再随机摸出一个球．两次都摸到黄球的概率是（ ）A、 B、 C、 D、4. 如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个小矩形．将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是（ ）
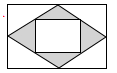A、 B、 C、 D、5. 每天登录“学习强国”App进行学习，在获得积分的同时，还可获得“点点通”附加奖励，李老师最近一周每日“点点通”收入明细如下表，则这组数据的中位数和众数分别是（ ）星期
一
二
三
四
五
六
日
收入（点）
15
21
27
27
21
30
21
A、27点，21点 B、21点，27点 C、21点，21点 D、24点，21点二、填空题
-
6. 要表示一个家庭一年用于“教育”， “服装”，“食品”，“其他”这四项的支出各占家庭本年总支出的百分比，从“扇形统计图”，“条形统计图”，“折线统计图”中选择一种统计图，最适合的统计图是.7. 某校为了选拔一名百米赛跑运动员参加市中学生运动会，组织了 次预选赛，其中甲，乙两名运动员较为突出，他们在 次预选赛中的成绩（单位：秒）如下表所示：
甲
乙
由于甲，乙两名运动员的成绩的平均数相同，学校决定依据他们成绩的稳定性进行选拔，那么被选中的运动员是 ．
三、综合题
-
8. 中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行，太原市作为主赛区，将承担多项赛事，现正从某高校的甲、乙两班分别招募10人作为颁奖礼仪志愿者，同学们踊跃报名，甲、乙两班各报了20人，现已对他们进行了基本素质测评，满分10分.各班按测评成绩从高分到低分顺序各录用10人，对这次基本素质测评中甲、乙两班学生的成绩绘制了如图所示的统计图.
请解答下列问题：
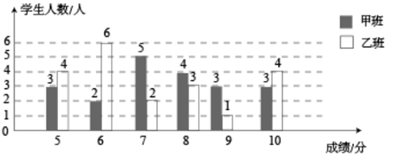(1)、甲班的小华和乙班的小丽基本素质测评成绩都为7分，请你分别判断小华，小丽能否被录用(只写判断结果，不必写理由).(2)、请你对甲、乙两班各被录用的10名志愿者的成绩作出评价(从“众数”，“中位数”，或“平均数”中的一个方面评价即可).(3)、甲、乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务，四个场馆分别为：太原学院足球场，太原市沙滩排球场，山西省射击射箭训练基地，太原水上运动中心，这四个场馆分别用字母A，B，C，D的四张卡片(除字母外，其余都相同)背面朝上，洗匀放好.志愿者小玲从中随机抽取一张(不放回)，再从中随机抽取一张，请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“A”和“B”的概率.9.从共享单车，共享汽车等共享出行到共享充电宝，共享雨伞等共享物品，各式各样的共享经济模式在各个领域迅速普及应用，越来越多的企业与个人成为参与者与受益者．根据国家信息中心发布的《中国分享经济发展报告2017》显示，2016年我国共享经济市场交易额约为34520亿元，比上年增长103%；超6亿人参与共享经济活动，比上年增加约1亿人．
如图是源于该报告中的中国共享经济重点领域市场规模统计图：
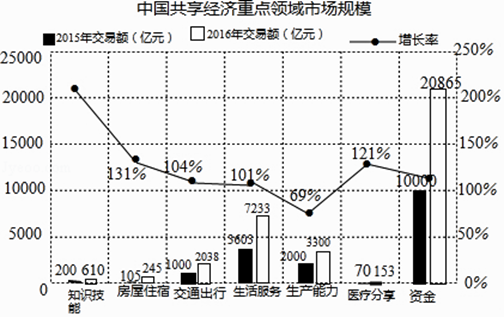(1)、请根据统计图解答下列问题：①图中涉及的七个重点领域中，2016年交易额的中位数是亿元．
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率（精确到1%），并就这两个重点领域中的一个分别从交易额和增长率两个方面，谈谈你的认识．
(2)、小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣，他们上网查阅了相关资料，顺便收集到四个共享经济领域的图标，并将其制成编号为A，B，C，D的四张卡片（除编号和内容外，其余完全相同）他们将这四张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张，请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率（这四张卡片分别用它们的编号A，B，C，D表示）
10. 在“优秀传统文化进校园”活动中，学校计划每周二下午第三节课时间开展此项活动，拟开展活动项目为：剪纸，武术，书法，器乐，要求七年级学生人人参加，并且每人只能参加其中一项活动．教务处在该校七年级学生中随机抽取了100名学生进行调查，并对此进行统计，绘制了如图所示的条形统计图和扇形统计图（均不完整）．
请解答下列问题：
(1)、请补全条形统计图和扇形统计图；
(2)、在参加“剪纸”活动项目的学生中，男生所占的百分比是多少？(3)、若该校七年级学生共有500人，请估计其中参加“书法”项目活动的有多少人？
(4)、学校教务处要从这些被调查的女生中，随机抽取一人了解具体情况，那么正好抽到参加“器乐”活动项目的女生的概率是多少？11. 年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通， 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等．《 新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域（ 基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩）总体的人才与就业机会．下图是其中的一个统计图．请根据图中信息，解答下列问题：
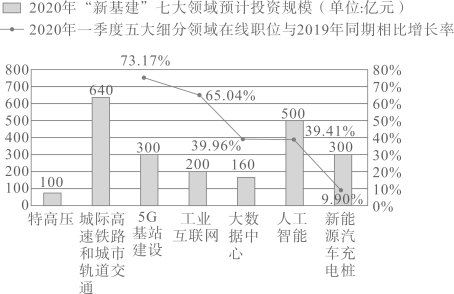(1)、填空：图中 年“新基建”七大领域预计投资规模的中位数是亿元；(2)、甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“ 基站建设”和“人工智能”作为自己的就业方向，请简要说明他们选择就业方向的理由各是什么；(3)、小勇对“新基建”很感兴趣，他收集到了五大细分领域的图标，依次制成编号为 ， ， ， ， 的五张卡片（除编号和内容外，其余完全相同），将这五张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画树状图的方法求抽到的两张卡片恰好是编号为 （ 基站建设）和 （人工智能）的概率．
12. 近日，教育部印发了《关于举办第三届中华经典诵写讲大赛的通知》，本届大赛以“传承中华经典，庆祝建党百年”为主题，分为“诵读中国”经典通读，“诗教中国”诗词讲解，“笔墨中国”汉字书写，“印记中国”印章篆刻比赛四类（依次记为 ， ， ， ）．为了解同学们参与这四类比赛的意向，某校学生会从有意向参与比赛的学生中随机抽取若干名学生进行了问卷调查（调查问卷如图所示），所有问卷全部收回，并将调查结果绘制成如下所示的统计图和统计表（均不完整）．请根据图表提供的信息，解答下列问题：
(1)、参与本次问卷调查的总人数为人，统计表中 的百分比 为；(2)、请补全统计图；(3)、小华想用扇形统计图反映有意向参与各类比赛的人数占被调查总人数的百分比，是否可行？若可行，求出表示 类比赛的扇形圆心角的度数；若不可行，请说明理由；(4)、学校“诗教中国”诗词讲解大赛初赛的规则是：组委会提供“春”“夏”“秋”“冬”四组题目（依次记为 ， ， ， ），由电脑随机给每位参赛选手派发一组，选手根据题目要求进行诗词讲解．请用列表或画树状图的方法求甲，乙两名选手抽到的题目在同一组的概率．