山西省中考数学真题汇编(近几年) 5 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
2. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( ) A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似3. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似3. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、
4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、 B、
B、 C、
C、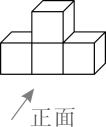 D、
D、 5. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
5. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )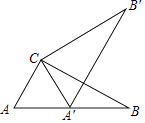 A、12 B、6 C、6 D、6. 如图,在矩形纸片 中, , ,点F是 上一点,点E在 上,将矩形纸片沿直线 折叠,点A落在点 处.点B恰好落在边 上的点 处, 交 于点G,若 ,则四边形 的面积等于( )
A、12 B、6 C、6 D、6. 如图,在矩形纸片 中, , ,点F是 上一点,点E在 上,将矩形纸片沿直线 折叠,点A落在点 处.点B恰好落在边 上的点 处, 交 于点G,若 ,则四边形 的面积等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通.如图是该地铁某站扶梯的示意图,扶梯 的坡度 ( 为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端 以0.5米/秒的速度用时40秒到达扶梯顶端 ,则王老师上升的铅直高度 为米.
 8. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
8. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .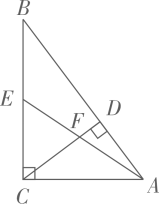 9.
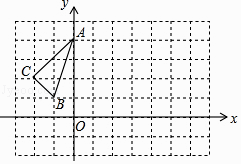
9.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 .
 10.
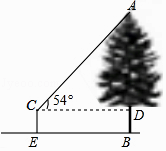
10.如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)
 11. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm.
11. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm.
三、解答题
-
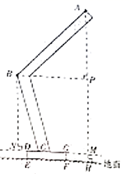
12. 某公园为引导游客观光游览公园的景点,在主要路口设置了导览指示牌.某校“综合与实践”活动小组想要测量此指示牌的高度,他们绘制了该指示牌支架侧面的截面图如图所示,并测得 , , , ,四边形 为矩形,且 .请帮助该小组求出指示牌最高点 到地面 的距离(结果精确到 .参考数据: , , , ).

四、综合题
-
13. 请阅读下列材料,并完成相应的任务:
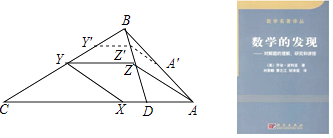
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y,使得AX=BY=XY.(如图)解决这个问题的操作步骤如下:
第一步,在CA上作出一点D,使得CD=CB,连接BD.第二步,在CB上取一点Y',作Y'Z'∥CA,交BD于点Z',并在AB上取一点A',使Z'A'=Y'Z'.第三步,过点A作AZ∥A'Z',交BD于点Z.第四步,过点Z作ZY∥AC,交BC于点Y,再过点Y作YX∥ZA,交AC于点X.
则有AX=BY=XY.
下面是该结论的部分证明:
证明:∵AZ∥A'Z',∴∠BA'Z'=∠BAZ,
又∵∠A'BZ'=∠ABZ.∴△BA'Z'~△BAZ.
∴ .
同理可得 .∴ .
∵Z'A'=Y'Z',∴ZA=YZ.
任务:
(1)、请根据上面的操作步骤及部分证明过程,判断四边形AXYZ的形状,并加以证明;(2)、请再仔细阅读上面的操作步骤,在(1)的基础上完成AX=BY=XY的证明过程;(3)、上述解决问题的过程中,通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY,从而确定了点Z,Y的位置,这里运用了下面一种图形的变化是 .A、平移 B、旋转 C、轴对称 D、位似14. 祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.项目
内容
课题
测量斜拉索顶端到桥面的距离
测量示意图
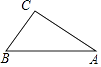
说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内.
测量数据
∠A的度数
∠B的度数
AB的长度
38°
28°
234米
…
…
 (1)、请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)(2)、该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).15.
(1)、请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)(2)、该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).15.综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3 ,4 ,5 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
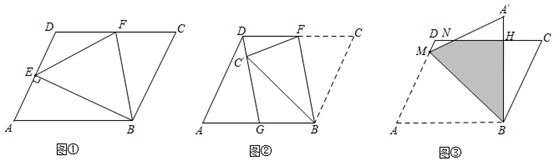
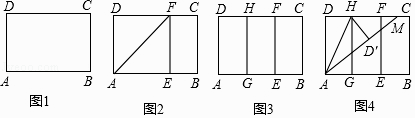 (1)、请在图2中证明四边形AEFD是正方形.(2)、请在图4中判断NF与ND′的数量关系,并加以证明;(3)、请在图4中证明△AEN(3,4,5)型三角形;(4)、在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.16. 综合与实践,问题情境:数学活动课上,老师出示了一个问题:如图①,在 中, ,垂足为 , 为 的中点,连接 , ,试猜想 与 的数量关系,并加以证明;
(1)、请在图2中证明四边形AEFD是正方形.(2)、请在图4中判断NF与ND′的数量关系,并加以证明;(3)、请在图4中证明△AEN(3,4,5)型三角形;(4)、在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.16. 综合与实践,问题情境:数学活动课上,老师出示了一个问题:如图①,在 中, ,垂足为 , 为 的中点,连接 , ,试猜想 与 的数量关系,并加以证明;独立思考:
(1)、请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将 沿着 ( 为 的中点)所在直线折叠,如图②,点 的对应点为 ,连接 并延长交 于点 ,请判断 与 的数量关系,并加以证明;
(3)、问题解决:智慧小组突发奇想,将 沿过点 的直线折叠,如图③,点A的对应点为 ,使 于点 ,折痕交 于点 ,连接 ,交 于点 .该小组提出一个问题:若此 的面积为20,边长 , ,求图中阴影部分(四边形 )的面积.请你思考此问题,直接写出结果.
 17. 阅读与思考,请阅读下列科普材料,并完成相应的任务.
17. 阅读与思考,请阅读下列科普材料,并完成相应的任务.图算法
图算法也叫诺模图,是根据几何原理,将某一已知函数关系式中的各变量,分别编成有刻度的直线(或曲线),并把它们按一定的规律排列在一起的一种图形,可以用来解函数式中的未知量.比如想知道10摄氏度相当于多少华氏度,我们可根据摄氏温度与华氏温度之间的关系: 得出,当 时, .但是如果你的温度计上有华氏温标刻度,就可以从温度计上直接读出答案,这种利用特制的线条进行计算的方法就是图算法.

再看一个例子:设有两只电阻,分别为5千欧和7.5千欧,问并联后的电阻值是多少?
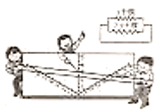
我们可以利用公式 求得 的值,也可以设计一种图算法直接得出结果:我们先来画出一个 的角,再画一条角平分线,在角的两边及角平分线上用同样的单位长度进行刻度,这样就制好了一张算图.我们只要把角的两边刻着7.5和5的两点连成一条直线,这条直线与角平分线的交点的刻度值就是并联后的电阻值.
图算法得出的数据大多是近似值,但在大多数情况下是够用的,那些需要用同一类公式进行计算的测量制图人员,往往更能体会到它的优越性.
任务:
(1)、请根据以上材料简要说明图算法的优越性;(2)、请用以下两种方法验证第二个例子中图算法的符合题意性:①用公式 计算:当 , 时, 的值为多少;
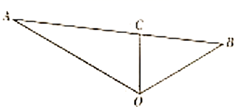
②如图,在 中, , 是 的角平分线, , ,用你所学的几何知识求线段 的长.
-