山西省中考数学真题汇编(近几年) 4 图形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是( )
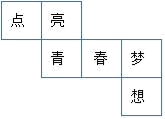 A、青 B、春 C、梦 D、想2. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( )
A、青 B、春 C、梦 D、想2. 如图,正六边形 的边长为2,以 为圆心, 的长为半径画弧,得 ,连接 , ,则图中阴影部分的面积为( ) A、 B、 C、 D、3. 如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A、 B、 C、 D、3. 如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )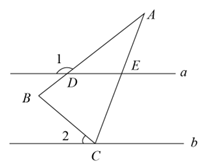 A、30° B、35° C、40° D、45°4. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A、30° B、35° C、40° D、45°4. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )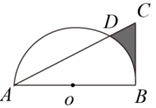 A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )
A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )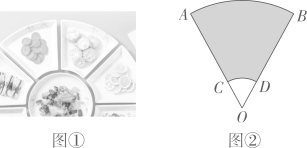 A、 B、 C、 D、6. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A、 B、 C、 D、6. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
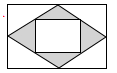 A、 B、 C、 D、7. 如图,在 中, 切 于点 ,连接 交 于点 ,过点 作 交 于点 ,连接 .若 ,则 为( )
A、 B、 C、 D、7. 如图,在 中, 切 于点 ,连接 交 于点 ,过点 作 交 于点 ,连接 .若 ,则 为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
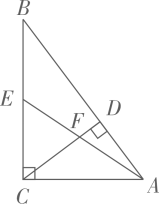 9. 如图,在菱形 中,对角线 , 相交于点 , , , ,交 于点 ,则 的长为 .
9. 如图,在菱形 中,对角线 , 相交于点 , , , ,交 于点 ,则 的长为 .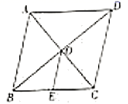 10. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .
10. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作⊙O,⊙O分别与AC,BC交于点E,F,过点F作⊙O的切线FG,交AB于点G,则FG的长为 .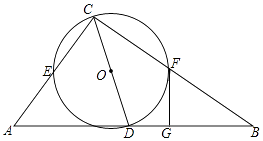 11. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm.
11. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm. 12. 如图,在 中,点 是 边上的一点,且 ,连接 并取 的中点 ,连接 ,若 ,且 ,则 的长为 .
12. 如图,在 中,点 是 边上的一点,且 ,连接 并取 的中点 ,连接 ,若 ,且 ,则 的长为 .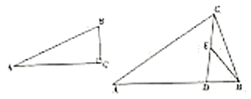
三、解答题
-
13. 已知:如图,点B,D在线段AE上,AD=BE,AC∥EH,∠C=∠H.求证:BC=DH.
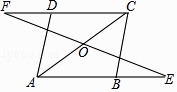
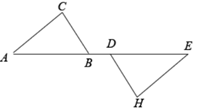 14. 已知:如图,在▱ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.
14. 已知:如图,在▱ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.求证:OE=OF.
 15. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
15. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.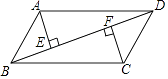 16. 如图,四边形 是平行四边形,以点 为圆心, 为半径的 与 相切于点 ,与 相交于点 , 的延长线交 于点 ,连接 交 于点 ,求 和 的度数.
16. 如图,四边形 是平行四边形,以点 为圆心, 为半径的 与 相切于点 ,与 相交于点 , 的延长线交 于点 ,连接 交 于点 ,求 和 的度数.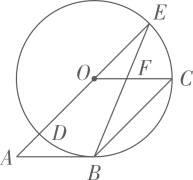
四、作图题
-
17. 阅读与思考
下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过 上的一点 ,作出 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?
办法一:如图①,可利用一把有刻度的直尺在 上量出 ,然后分别以 , 为圆心,以 与 为半径画圆弧,两弧相交于点 ,作直线 ,则 必为 .

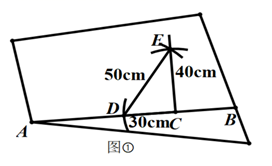
办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 , 两点,然后把木棒斜放在木板上,使点 与点 重合,用铅笔在木板上将点 对应的位置标记为点 ,保持点 不动,将木棒绕点 旋转,使点 落在 上,在木板上将点 对应的位置标记为点 .然后将 延长,在延长线上截取线段 ,得到点 ,作直线 ,则 .
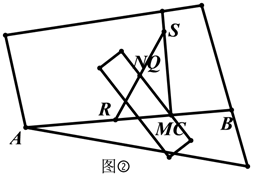
我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢?
……
任务:
(1)、填空;“办法一”依据的一个数学定理是;(2)、根据“办法二”的操作过程,证明 ;(3)、①尺规作图:请在图③的木板上,过点 作出 的垂线(在木板上保留作图痕迹,不写作法);②说明你的作法依据的数学定理或基本事实(写出一个即可)
五、综合题
-
18. 综合与实践
动手操作:
第一步:如图1,正方形纸片ABCD沿对角线AC所在直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一直线上,折痕分别为CE,CF.如图2.
第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3
第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的虚线为折痕.
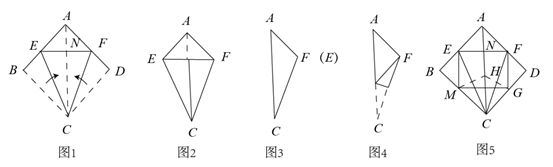
问题解决:
(1)、在图5中,∠BEC的度数是 , 的值是;(2)、在图5中,请判断四边形EMGF的形状,并说明理由;(3)、在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形:19. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)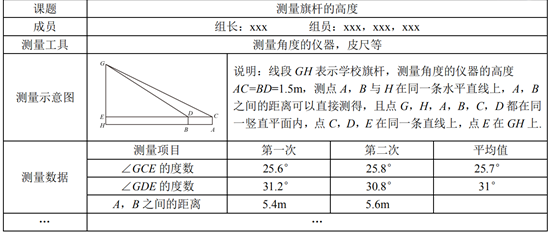
 (1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(3)、任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).20. 阅读以下材料,并按要求完成相应地任务:莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,


任务:
(1)、观察发现: , (用含R,d的代数式表示);(2)、请判断BD和ID的数量关系,并说明理由;(3)、请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;(4)、应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为cm.21. 综合与实践问题情境:
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 ),延长 交 于点 ,连接 .
猜想证明:
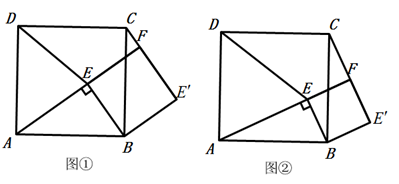 (1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;
(1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;解决问题:
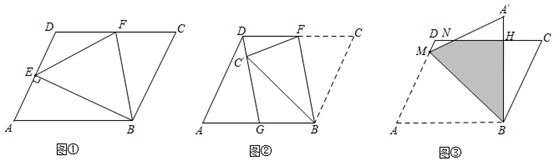
(3)、如图①,若 , ,请直接写出 的长.22. 综合与实践,问题情境:数学活动课上,老师出示了一个问题:如图①,在 中, ,垂足为 , 为 的中点,连接 , ,试猜想 与 的数量关系,并加以证明;独立思考:
(1)、请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将 沿着 ( 为 的中点)所在直线折叠,如图②,点 的对应点为 ,连接 并延长交 于点 ,请判断 与 的数量关系,并加以证明;
(3)、问题解决:智慧小组突发奇想,将 沿过点 的直线折叠,如图③,点A的对应点为 ,使 于点 ,折痕交 于点 ,连接 ,交 于点 .该小组提出一个问题:若此 的面积为20,边长 , ,求图中阴影部分(四边形 )的面积.请你思考此问题,直接写出结果.
-