山西省中考数学真题汇编(近几年) 3 函数
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 已知反比例函数 ,则下列描述错误的是( )A、图象位于第一,第三象限 B、图象必经过点 C、图象不可能与坐标轴相交 D、 随 的增大而减小2. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、3. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、4. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、5. 北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
 A、 B、 C、 D、6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x﹣4)2﹣25 C、y=(x+4)2+7 D、y=(x+4)2﹣257. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( )
A、 B、 C、 D、6. 用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )A、y=(x﹣4)2+7 B、y=(x﹣4)2﹣25 C、y=(x+4)2+7 D、y=(x+4)2﹣257. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( ) A、A→O→B B、B→A→C C、B→O→C D、C→B→O
A、A→O→B B、B→A→C C、B→O→C D、C→B→O二、填空题
-
8. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部” , 两点的坐标分别为 , ,则叶杆“底部”点 的坐标为 .
 9. 如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数 的图象恰好经过点C,则k的值为.
9. 如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数 的图象恰好经过点C,则k的值为.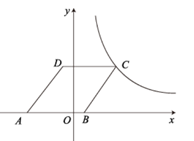
三、综合题
-
10. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y= (k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.
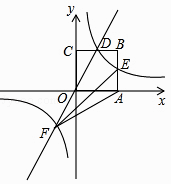 (1)、求函数y= 的表达式,并直接写出E、F两点的坐标;(2)、求△AEF的面积.11.
(1)、求函数y= 的表达式,并直接写出E、F两点的坐标;(2)、求△AEF的面积.11.如图,抛物线y=﹣ x2+ x+3 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
 (1)、求直线BC的函数表达式;(2)、①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
(1)、求直线BC的函数表达式;(2)、①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)、试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.12. 如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2= 的图象相交于点C(﹣4,﹣2),D(2,4). (1)、求一次函数和反比例函数的表达式;
(1)、求一次函数和反比例函数的表达式;
(2)、当x为何值时,y1>0;(3)、当x为何值时,y1<y2 , 请直接写出x的取值范围.
13. 综合与探究如图,抛物线y= 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.
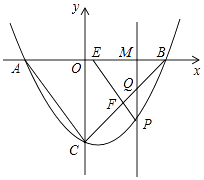 (1)、求A,B,C三点的坐标
(1)、求A,B,C三点的坐标
(2)、试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)、请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.14. 综合与探究如图,抛物线 经过点A(-2,0),B(4,0)两点,与 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为 .连接AC,BC,DB,DC.
 (1)、求抛物线的函数表达式;(2)、△BCD的面积等于△AOC的面积的 时,求 的值;(3)、在(2)的条件下,若点M是 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.15. 综合与探究
(1)、求抛物线的函数表达式;(2)、△BCD的面积等于△AOC的面积的 时,求 的值;(3)、在(2)的条件下,若点M是 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.15. 综合与探究如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 .直线 与抛物线交于 , 两点,与 轴交于点 ,点 的坐标为 .
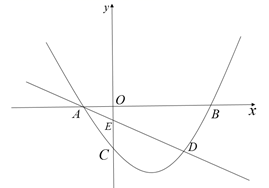 (1)、请直接写出 , 两点的坐标及直线 的函数表达式;(2)、若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 . 与直线 交于点 ,当点 是线段 的三等分点时,求点 的坐标;(3)、若点 是 轴上的点,且 ,求点 的坐标.16. 如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,连接 , .
(1)、请直接写出 , 两点的坐标及直线 的函数表达式;(2)、若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 . 与直线 交于点 ,当点 是线段 的三等分点时,求点 的坐标;(3)、若点 是 轴上的点,且 ,求点 的坐标.16. 如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,连接 , . (1)、求 , , 三点的坐标并直接写出直线 , 的函数表达式;(2)、点 是直线 下方抛物线上的一个动点,过点 作 的平行线 ,交线段 于点 .
(1)、求 , , 三点的坐标并直接写出直线 , 的函数表达式;(2)、点 是直线 下方抛物线上的一个动点,过点 作 的平行线 ,交线段 于点 .①试探究:在直线 上是否存在点 ,使得以点 , , , 为顶点的四边形为菱形,若存在,求出点 的坐标;若不存在,请说明理由;
②设抛物线的对称轴与直线 交于点 ,与直线 交于点 .当 时,请直接写出 的长.