河北省中考数学真题汇编(近几年) 5 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,从点C观测点D的仰角是( )
2. 如图,从点C观测点D的仰角是( )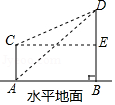 A、∠DAB B、∠DCE C、∠DCA D、∠ADC3. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )
A、∠DAB B、∠DCE C、∠DCA D、∠ADC3. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )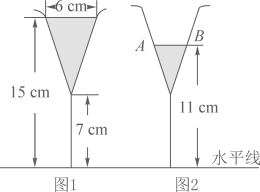 A、 B、 C、 D、4. 如图,直线 , 相交于点 . 为这两直线外一点,且 .若点 关于直线 , 的对称点分别是点 , ,则 , 之间的距离可能是( )
A、 B、 C、 D、4. 如图,直线 , 相交于点 . 为这两直线外一点,且 .若点 关于直线 , 的对称点分别是点 , ,则 , 之间的距离可能是( ) A、0 B、5 C、6 D、75. 在如图所示的网格中,以点O为位似中心,四边形 的位似图形是( )
A、0 B、5 C、6 D、75. 在如图所示的网格中,以点O为位似中心,四边形 的位似图形是( )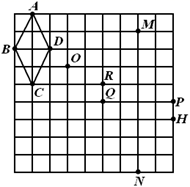 A、四边形 B、四边形 C、四边形 D、四边形6. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A、四边形 B、四边形 C、四边形 D、四边形6. 如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )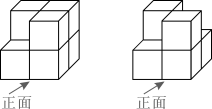 A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同7. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同7. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( ) A、4.5 B、4 C、3 D、28. 图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
A、4.5 B、4 C、3 D、28. 图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )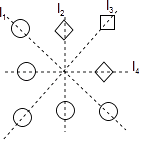 A、l1 B、l2 C、l3 D、l49. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )
A、l1 B、l2 C、l3 D、l49. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( ) A、① B、② C、③ D、④10. 如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )
A、① B、② C、③ D、④10. 如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 11.
11.如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
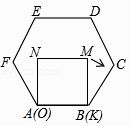
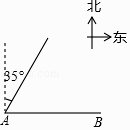 A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°12. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°12. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
 A、1.4 B、1.1 C、0.8 D、0.513. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n . ”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x , 再取最小整数n .
A、1.4 B、1.1 C、0.8 D、0.513. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n . ”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x , 再取最小整数n .甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取n=13.
乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取n=14.
丙:如图4,思路是当x为矩形的长与宽之和的 倍时就可移转过去;结果取n=13.
下列正确的是( )
 A、甲的思路错,他的n值对 B、乙的思路和他的n值都对 C、甲和丙的n值都对 D、甲、乙的思路都错,而丙的思路对
A、甲的思路错,他的n值对 B、乙的思路和他的n值都对 C、甲和丙的n值都对 D、甲、乙的思路都错,而丙的思路对二、综合题
-
14. 下图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点 )始终以 的速度在离地面 高的上空匀速向右飞行,2号试飞机(看成点 )一直保持在1号机 的正下方 , 2号机从原点 处沿 仰角爬升,到 高的 处便立刻转为水平飞行,再过 到达 处开始沿直线 降落,要求 后到达 处.
 (1)、求 的 关于 的函数解析式,并直接写出2号机的爬升速度;(2)、求 的 关于 的函数解析式,并预计2号机着陆点的坐标;(3)、通过计算说明两机距离 不超过 的时长是多少.
(1)、求 的 关于 的函数解析式,并直接写出2号机的爬升速度;(2)、求 的 关于 的函数解析式,并预计2号机着陆点的坐标;(3)、通过计算说明两机距离 不超过 的时长是多少.(注:(1)及(2)中不必写 的取值范围)
15.平面内,如图,在▱ABCD中,AB=10,AD=15,tanA= ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
 (1)、当∠DPQ=10°时,求∠APB的大小;(2)、当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);(3)、若点Q恰好落在▱ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)16. 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 于点P,Q,且点P,Q在AB异侧,连接OP.
(1)、当∠DPQ=10°时,求∠APB的大小;(2)、当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);(3)、若点Q恰好落在▱ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)16. 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 于点P,Q,且点P,Q在AB异侧,连接OP.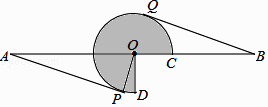 (1)、求证:AP=BQ;(2)、当BQ=4 时,求 的长(结果保留π);(3)、若△APO的外心在扇形COD的内部,求OC的取值范围.17. 如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M , 其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.
(1)、求证:AP=BQ;(2)、当BQ=4 时,求 的长(结果保留π);(3)、若△APO的外心在扇形COD的内部,求OC的取值范围.17. 如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M , 其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.发现 AP(弧)的长与QB(弧)的长之和为定值l , 求l;
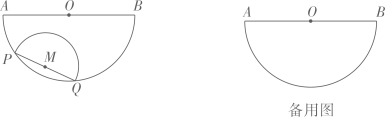 (1)、【思考】
(1)、【思考】点M与AB的最大距离为 , 此时点P , A间的距离为;点M与AB的最小距离为 , 此时半圆M的弧与AB所围成的封闭图形面积为.
(2)、【探究】当半圆M与AB相切时,求AP(弧)的长.
(注:结果保留π,cos 35°= ,cos 55°= )
18. 如图1和图2,在 中, , , .点K在 边上,点M,N分别在 , 上,且 .点P从点M出发沿折线 匀速移动,到达点N时停止;而点Q在 边上随P移动,且始终保持 .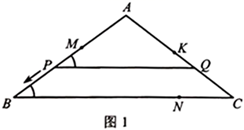
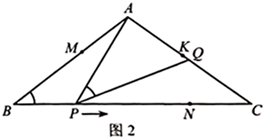 (1)、当点P在 上时,求点P与点A的最短距离;(2)、若点P在 上,且 将 的面积分成上下4:5两部分时,求 的长;(3)、设点 移动的路程为x,当 及 时,分别求点P到直线 的距离(用含x的式子表示);(4)、在点 处设计并安装一扫描器,按定角 扫描 区域(含边界),扫描器随点P从M到B再到N共用时36秒.若 ,请直接写出点K被扫描到的总时长.19. 如图1和2,▱ABCD中,AB=3,BC=15,tan∠DAB= .点P为AB延长线上一点,过点A作⊙O切CP于点P , 设BP=x .
(1)、当点P在 上时,求点P与点A的最短距离;(2)、若点P在 上,且 将 的面积分成上下4:5两部分时,求 的长;(3)、设点 移动的路程为x,当 及 时,分别求点P到直线 的距离(用含x的式子表示);(4)、在点 处设计并安装一扫描器,按定角 扫描 区域(含边界),扫描器随点P从M到B再到N共用时36秒.若 ,请直接写出点K被扫描到的总时长.19. 如图1和2,▱ABCD中,AB=3,BC=15,tan∠DAB= .点P为AB延长线上一点,过点A作⊙O切CP于点P , 设BP=x .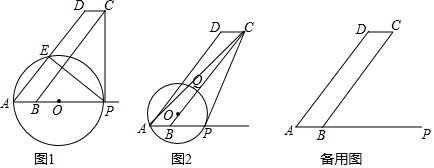 (1)、如图1,x为何值时,圆心O落在AP上?若此时⊙O交AD于点E , 直接指出PE与BC的位置关系;(2)、当x=4时,如图2,⊙O与AC交于点Q , 求∠CAP的度数,并通过计算比较弦AP与劣弧 长度的大小;(3)、当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.20. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
(1)、如图1,x为何值时,圆心O落在AP上?若此时⊙O交AD于点E , 直接指出PE与BC的位置关系;(2)、当x=4时,如图2,⊙O与AC交于点Q , 求∠CAP的度数,并通过计算比较弦AP与劣弧 长度的大小;(3)、当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.20. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.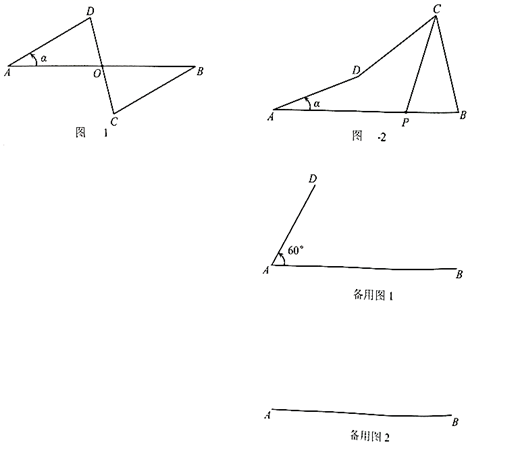 (1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
(1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);②当点 在 下方,且 与 垂直时,直接写出 的余弦值.