河北省中考数学真题汇编(近几年) 4 图形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如图,菱形ABCD中,∠D=150°,则∠1=( )
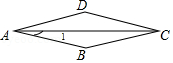 A、30° B、25° C、20° D、15°2. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A、30° B、25° C、20° D、15°2. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )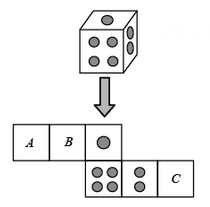 A、 代表
A、 代表 B、 代表
B、 代表  C、 代表
C、 代表  D、 代表
D、 代表  3. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( )
3. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( ) A、 B、 C、 D、4. 如图1, 中, , 为锐角.要在对角线 上找点 , ,使四边形 为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
A、 B、 C、 D、4. 如图1, 中, , 为锐角.要在对角线 上找点 , ,使四边形 为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )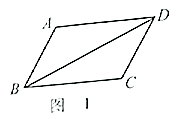
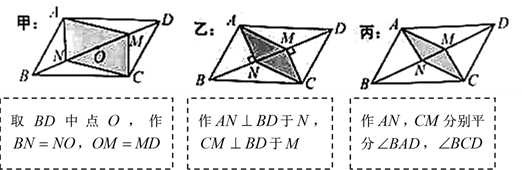
图2
A、甲、乙、丙都是 B、只有甲、乙才是 C、只有甲、丙才是 D、只有乙、丙才是5. 如图,点 为正六边形 对角线 上一点, , ,则 的值是( )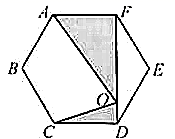 A、20 B、30 C、40 D、随点 位置而变化6. 如图,等腰 中,顶角 ,用尺规按①到④的步骤操作:
A、20 B、30 C、40 D、随点 位置而变化6. 如图,等腰 中,顶角 ,用尺规按①到④的步骤操作: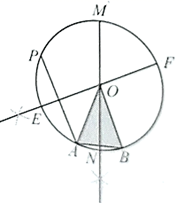
①以 为圆心, 为半径画圆;
②在 上任取一点 (不与点 , 重合),连接 ;
③作 的垂直平分线与 交于 , ;
④作 的垂直平分线与 交于 , .
结论Ⅰ:顺次连接 , , , 四点必能得到矩形;
结论Ⅱ: 上只有唯一的点 ,使得 .
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对7. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )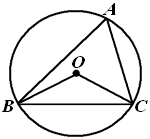 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( ) A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,49. 如图,从笔直的公路 旁一点P出发,向西走 到达 ;从P出发向北走 也到达l.下列说法错误的是( )
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,49. 如图,从笔直的公路 旁一点P出发,向西走 到达 ;从P出发向北走 也到达l.下列说法错误的是( )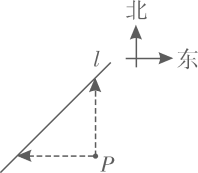 A、从点P向北偏西45°走 到达l B、公路l的走向是南偏西45° C、公路l的走向是北偏东45° D、从点P向北走 后,再向西走 到达l10. 如图1,已知 ,用尺规作它的角平分线.
A、从点P向北偏西45°走 到达l B、公路l的走向是南偏西45° C、公路l的走向是北偏东45° D、从点P向北走 后,再向西走 到达l10. 如图1,已知 ,用尺规作它的角平分线.如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线 BA , BC 于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在 内部交于点P;
第三步:画射线 BP .射线 BP 即为所求.
下列正确的是( )
 A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长11. 如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下:
A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长11. 如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下:点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
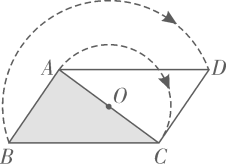
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是( )
A、嘉淇推理严谨,不必补充 B、应补充:且 , C、应补充:且 D、应补充:且 ,12. 如图,在平面内作已知直线m的垂线,可作垂线的条数有( ) A、0条 B、1条 C、2条 D、无数条13. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n . ”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x , 再取最小整数n .
A、0条 B、1条 C、2条 D、无数条13. 对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n . ”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x , 再取最小整数n .甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取n=13.
乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取n=14.
丙:如图4,思路是当x为矩形的长与宽之和的 倍时就可移转过去;结果取n=13.
下列正确的是( )
 A、甲的思路错,他的n值对 B、乙的思路和他的n值都对 C、甲和丙的n值都对 D、甲、乙的思路都错,而丙的思路对14. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容
A、甲的思路错,他的n值对 B、乙的思路和他的n值都对 C、甲和丙的n值都对 D、甲、乙的思路都错,而丙的思路对14. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容
则回答正确的是( )
A、◎代表∠FEC B、@代表同位角 C、▲代表∠EFC D、※代表AB15. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图, 是 的外角.
求证: .



下列说法正确的是( )
A、证法1还需证明其他形状的三角形,该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证,就能证明该定理二、填空题
-
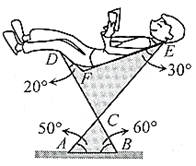
16. 正六边形的一个内角是正n边形一个外角的4倍,则n= .17. 下图是可调躺椅示意图(数据如图), 与 的交点为 ,且 , , 保持不变.为了舒适,需调整 的大小,使 ,则图中 应(填“增加”或“减少”)度.
 18. 如图,依据尺规作图的痕迹,计算∠α=°.
18. 如图,依据尺规作图的痕迹,计算∠α=°.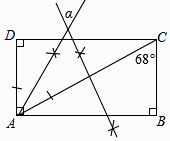 19. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为m.
19. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为m. 20. 如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而 =45是360°(多边形外角和)的 ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
20. 如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而 =45是360°(多边形外角和)的 ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.

图2中的图案外轮廓周长是;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是 .
三、综合题
-
21. 如图1和2,▱ABCD中,AB=3,BC=15,tan∠DAB= .点P为AB延长线上一点,过点A作⊙O切CP于点P , 设BP=x .
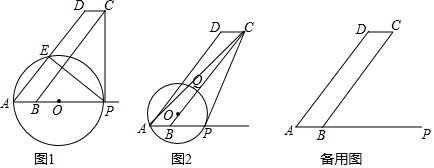 (1)、如图1,x为何值时,圆心O落在AP上?若此时⊙O交AD于点E , 直接指出PE与BC的位置关系;(2)、当x=4时,如图2,⊙O与AC交于点Q , 求∠CAP的度数,并通过计算比较弦AP与劣弧 长度的大小;(3)、当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.22. 如图,△ABC和△ADE中,AB=AD=6,BC=DE , ∠B=∠D=30°,边AD与边BC交于点P(不与点B , C重合),点B , E在AD异侧,I为△APC的内心.
(1)、如图1,x为何值时,圆心O落在AP上?若此时⊙O交AD于点E , 直接指出PE与BC的位置关系;(2)、当x=4时,如图2,⊙O与AC交于点Q , 求∠CAP的度数,并通过计算比较弦AP与劣弧 长度的大小;(3)、当⊙O与线段AD只有一个公共点时,直接写出x的取值范围.22. 如图,△ABC和△ADE中,AB=AD=6,BC=DE , ∠B=∠D=30°,边AD与边BC交于点P(不与点B , C重合),点B , E在AD异侧,I为△APC的内心. (1)、求证:∠BAD=∠CAE;(2)、设AP=x , 请用含x的式子表示PD , 并求PD的最大值;(3)、当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m , n的值.23. 如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)、求证:∠BAD=∠CAE;(2)、设AP=x , 请用含x的式子表示PD , 并求PD的最大值;(3)、当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m , n的值.23. 如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.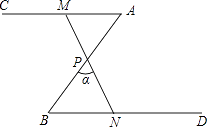 (1)、求证:△APM≌△BPN;(2)、当MN=2BN时,求α的度数;(3)、若△BPN的外心在该三角形的内部,直接写出α的取值范围.24. 如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧 ,使点B在O右下方,且tan∠AOB= ,在优弧 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)、求证:△APM≌△BPN;(2)、当MN=2BN时,求α的度数;(3)、若△BPN的外心在该三角形的内部,直接写出α的取值范围.24. 如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧 ,使点B在O右下方,且tan∠AOB= ,在优弧 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.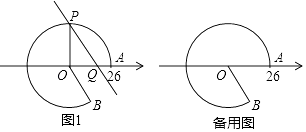 (1)、若优弧上一段 的长为13π,求∠AOP的度数及x的值;(2)、求x的最小值,并指出此时直线l与 所在圆的位置关系;(3)、若线段PQ的长为12.5,直接写出这时x的值.25. 如图,点O为 中点,分别延长 到点C, 到点D,使 .以点O为圆心,分别以 , 为半径在 上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接 并延长交大半圆于点E,连接 , .
(1)、若优弧上一段 的长为13π,求∠AOP的度数及x的值;(2)、求x的最小值,并指出此时直线l与 所在圆的位置关系;(3)、若线段PQ的长为12.5,直接写出这时x的值.25. 如图,点O为 中点,分别延长 到点C, 到点D,使 .以点O为圆心,分别以 , 为半径在 上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接 并延长交大半圆于点E,连接 , .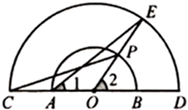
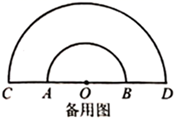 (1)、①求证: ;
(1)、①求证: ;②写出∠1,∠2和 三者间的数量关系,并说明理由.
(2)、若 ,当 最大时,直接指出 与小半圆的位置关系,并求此时 (答案保留 ).26. 如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 ( 为1~12的整数),过点 作 的切线交 延长线于点 . (1)、通过计算比较直径和劣弧 长度哪个更长;(2)、连接 ,则 和 有什么特殊位置关系?请简要说明理由;(3)、求切线长 的值.27. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
(1)、通过计算比较直径和劣弧 长度哪个更长;(2)、连接 ,则 和 有什么特殊位置关系?请简要说明理由;(3)、求切线长 的值.27. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.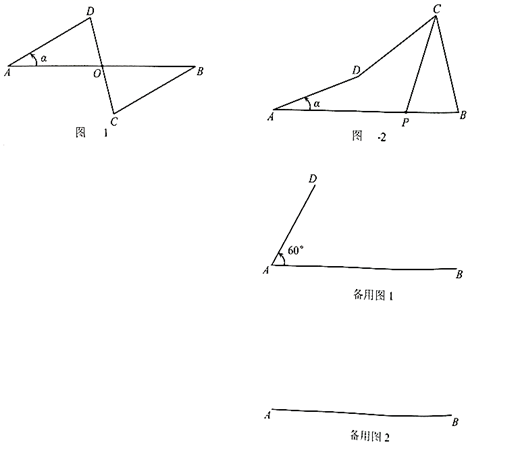 (1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
(1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);②当点 在 下方,且 与 垂直时,直接写出 的余弦值.