河北省中考数学真题汇编(近几年) 2 方程与不等式
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 已知 ,则一定有 ,“ ”中应填的符号是( )A、 B、 C、 D、2. 语句“x的 与x的和不超过5”可以表示为( )A、 +x≤5 B、 +x≥5 C、 ≤5 D、 +x=53. 有三种不同质量的物体“
 ”“
”“  ”“
”“  ”,其中,同一种物体的质量都相等,现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是( )
”,其中,同一种物体的质量都相等,现左右手中同样的盘子上都放着不同个数的物体,只有一组左右质量不相等,则该组是( )
A、 B、
B、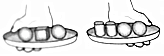 C、
C、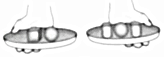 D、
D、 4. 对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
4. 对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
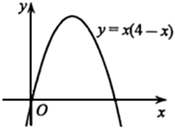
A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确5. 小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=﹣1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有一个根是x=﹣1 D、有两个相等的实数根6. 如图,现要在抛物线 上找点 ,针对b的不同取值,所找点P的个数,三人的说法如下,甲:若 ,则点P的个数为0;
乙:若 ,则点P的个数为1;
丙:若 ,则点P的个数为1.
下列判断正确的是( )
 A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对7. 有一题目:点P、Q、M分别表示数-1、1、5,三点在数轴上同时开始运动,点P运动方向是向左,运动速度是 ;点Q、M的运动方向是向右,运动速度分别 、 ,如图,在运动过程中,甲、乙两位同学提出不同的看法,甲: 的值不变;乙: 的值不变;下列选项中,正确的是( )
A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对7. 有一题目:点P、Q、M分别表示数-1、1、5,三点在数轴上同时开始运动,点P运动方向是向左,运动速度是 ;点Q、M的运动方向是向右,运动速度分别 、 ,如图,在运动过程中,甲、乙两位同学提出不同的看法,甲: 的值不变;乙: 的值不变;下列选项中,正确的是( ) A、甲、乙均正确 B、甲正确、乙错误 C、甲错误、乙正确 D、甲、乙均错误
A、甲、乙均正确 B、甲正确、乙错误 C、甲错误、乙正确 D、甲、乙均错误二、填空题
-
8. 对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ,﹣ }=;若min{(x﹣1)2 , x2}=1,则x= .
9. 如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.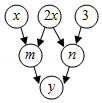
示例:
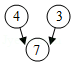 即4+3=7
即4+3=7则
(1)、用含x的式子表示m=;(2)、当y=﹣2时,n的值为 .10. 如图,在长方形 中,放入6个形状、大小都相同的长方形,所标尺寸如图所示,则图中阴影部分面积是 , 若平移这六个长方形,则图中剩余的阴影部分面积是否改变?(填“变”或“不变”).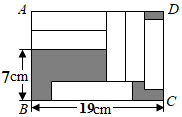
三、综合题
-
11. 已知训练场球筐中有 、 两种品牌的乒乓球共101个,设 品牌乒乓球有 个.(1)、淇淇说:“筐里 品牌球是 品牌球的两倍.”嘉嘉根据她的说法列出了方程: .请用嘉嘉所列方程分析淇淇的说法是否符合题意;(2)、据工作人员透露: 品牌球比 品牌球至少多28个,试通过列不等式的方法说明 品牌球最多有几个.12. 如图1,点 是数轴上:从左到右排列的三个点,分别对应的数为 某同学将刻度尺如图2放置.使刻度尺上的数字 对齐数轴上的点 ,发现点 对齐刻度 ,点 对齐刻度 .
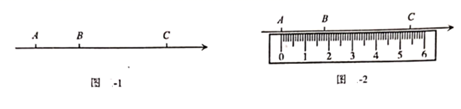 (1)、在图1的数轴上, 个单位长度;数轴上的一个单位长度对应刻度尺上的 .(2)、求数轴上点 所对应的数 ;(3)、在图1的数轴上,点 是线段 上一点,满足 求点 所表示的数.13. 阅读下面的学习材料:
(1)、在图1的数轴上, 个单位长度;数轴上的一个单位长度对应刻度尺上的 .(2)、求数轴上点 所对应的数 ;(3)、在图1的数轴上,点 是线段 上一点,满足 求点 所表示的数.13. 阅读下面的学习材料:我们知道,一般情况下式子 与“ ”是不相等的(m , n均为整数),但当m , n取某些特定整数时,可以使这两个式子相等,我们把使“ ”成立的数对“m , n”叫做“好数对”,记作[m , n],例如,当m=n=0时,有 成立,则数对“0,0”就是一对“好数对”,记作[0,0]
解答下列问题:
(1)、通过计算,判断数对“3,4”是否是“好数对”;(2)、求“好数对”[x , ﹣32]中x的值;(3)、请再写出一对上述未出现的“好数对”[ , ];(4)、对于“好数对[a , b],如果a=9k(k为整数),则b=(用含k的代数式表示).14. 某商人开始将进价为每件8元的某种商品按每件10元出售,每天售出100件;后来他利用提高售价的方法来增加利润,发现这种商品每提价1元,每天的销售量就会减少10件.(1)、他若想每天的利润达到350元,求此时的售价应为每件多少元?(2)、每天的利润能否达到380元?为什么?15. 随着出行方式的多样化,我市三类打车方式的收费标准如下:出租车
滴滴快车
同城快车
3千米以内:8元
路程:1.4元/千米
路程:1.8元/千米
超过3千米的部分:2.4元/千米
时间:0.6元/分钟
时间:0.4元/分钟
如:假设打车的平均车速为40千米/小时,乘坐8千米,耗时8÷40×60=12分钟,出租车的收费为:8+2.4×(8﹣3)=20(元);滴滴快车的收费为:8×1.4+12×0.6=18.4(元);同城快车的收费为:8×1.8+12×0.4=19.2(元)
解决问题:
(1)、小明乘车从高邮文体公园去盂城驿,全程10千米,如果小明使用滴滴快车,需要支付的打车费用为元;(2)、小丽乘车从甲地去乙地,用滴滴快车比乘坐出租车节省了28.8元,求甲、乙两地的距离;(3)、同城快车为了和滴滴快车竞争客户,分别推出了优惠方式:滴滴快车对于乘车路程在5千米以上(含5千米)的客户每次收费立减11元;同城快车车费对折优惠.通过计算,对同城快车和滴滴快车两种打车方式,采用哪一种打车方式更合算提出你的建议.