河北省中考数学真题模拟题近几年汇编 1 数与式

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，将数轴上-6与6两点间的线段六等分，这五个等分点所对应数依次为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ ，则下列正确的是（）

A、 $a_{3} > 0$ B、 $| a_{1} | = | a_{4} |$ C、 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = 0$ D、 $a_{2} + a_{5} < 0$

查看试题解析
2. 墨迹覆盖了等式“ $x^{3}$ $x = x^{2}$ （ $x \neq 0$ ）”中的运算符号，则覆盖的是（）

A、＋ B、－ C、× D、÷

查看试题解析
3. 若 $a \neq b$ ，则下列分式化简正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a - 2}{b - 2} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{\frac{1}{2} a}{\frac{1}{2} b} = \frac{a}{b}$

查看试题解析
4. 若k为正整数，则 ${(\underset{k 个 k}{\underset{︸}{k + k + \cdot \cdot \cdot + k}})}^{k} =$ （）

A、 $k^{2 k}$ B、 $k^{2 k + 1}$ C、 $2 k^{k}$ D、 $k^{2 + k}$

查看试题解析
5. 已知光速为300000千米秒，光经过t秒（ $1 \leq t \leq 10$ ）传播的距离用科学记数法表示为 $a \times 10^{n}$ 千米，则n可能为（）

A、5 B、6 C、5或6 D、5或6或7

查看试题解析
6. 若 $\frac{(9^{2} - 1) (11^{2} - 1)}{k} = 8 \times 10 \times 12$ ，则 $k =$ （）

A、12 B、10 C、8 D、6

查看试题解析
7. 对于① $x - 3 x y = x (1 - 3 y)$ ，② $(x + 3) (x - 1) = x^{2} + 2 x - 3$ ，从左到右的变形，表述正确的是（）

A、都是因式分解 B、都是乘法运算 C、①是因式分解，②是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
8. 不一定相等的一组是（）

A、 $a + b$ 与 $b + a$ B、 $3 a$ 与 $a + a + a$ C、 $a^{3}$ 与 $a \cdot a \cdot a$ D、 $3 (a + b)$ 与 $3 a + b$

查看试题解析
9. 若 $\sqrt[3]{3}$ 取1.442，计算 $\sqrt[3]{3} - 3 \sqrt[3]{3} - 98 \sqrt[3]{3}$ 的结果是（）

A、-100 B、-144.2 C、144.2 D、-0.01442

查看试题解析
10. 由 $(\frac{1 + c}{2 + c} - \frac{1}{2})$ 值的正负可以比较 $A = \frac{1 + c}{2 + c}$ 与 $\frac{1}{2}$ 的大小，下列正确的是（）

A、当 $c = - 2$ 时， $A = \frac{1}{2}$ B、当 $c = 0$ 时， $A \neq \frac{1}{2}$ C、当 $c < - 2$ 时， $A > \frac{1}{2}$ D、当 $c < 0$ 时， $A < \frac{1}{2}$

查看试题解析
11. 与 $\sqrt{3^{2} - 2^{2} - 1^{2}}$ 结果相同的是（）．

A、 $3 - 2 + 1$ B、 $3 + 2 - 1$ C、 $3 + 2 + 1$ D、 $3 - 2 - 1$

查看试题解析
12. 能与 $- (\frac{3}{4} - \frac{6}{5})$ 相加得0的是（）

A、 $- \frac{3}{4} - \frac{6}{5}$ B、 $\frac{6}{5} + \frac{3}{4}$ C、 $- \frac{6}{5} + \frac{3}{4}$ D、 $- \frac{3}{4} + \frac{6}{5}$

查看试题解析
13. 如图，若x为正整数，则表示 $\frac{{(x + 2)}^{2}}{x^{2} + 4 x + 4}$ ﹣ $\frac{1}{x + 1}$ 的值的点落在（）

A、段① B、段② C、段③ D、段④

查看试题解析
14. 图2是图1中长方体的三视图，若用S表示面积，S_主＝x²+2x ， S_左＝x²+x ，则S_俯＝（）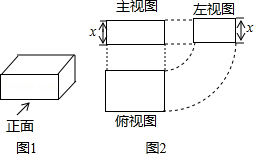

A、x²+3x+2 B、x²+2 C、x²+2x+1 D、2x²+3x

查看试题解析

二、填空题

15. 若7^﹣2×7^﹣1×7⁰＝7^p ，则p的值为．

查看试题解析
16. 已知： $\sqrt{18} - \sqrt{2} = a \sqrt{2} - \sqrt{2} = b \sqrt{2}$ ，则 $a b =$ ．

查看试题解析
17. 已知：整式A＝（n²﹣1）²+（2n）² ，整式B＞0．
尝试化简整式A ．

发现 A＝B² ，求整式B ．

联想由上可知，B²＝（n²﹣1）²+（2n）² ，当n＞1时，n²﹣1，2n ， B为直角三角形的三边长，如图．填写下表中B的值：

直角三角形三边

n²﹣1

2n

B

勾股数组Ⅰ

/

8

勾股数组Ⅱ

35

/

查看试题解析
18. 现有甲、乙、丙三种不同的矩形纸片（边长如图）．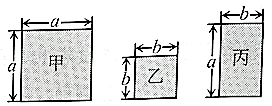

(1)、取甲、乙纸片各1块，其面积和为；

(2)、嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片1块，再取乙纸片4块，还需取丙纸片块．

查看试题解析

三、计算题

19. 已知两个有理数：－9和5．

(1)、计算： $\frac{(- 9) + 5}{2}$ ；

(2)、若再添一个负整数 $m$ ，且－9，5与 $m$ 这三个数的平均数仍小于m，求m的值．

查看试题解析

四、综合题

20. 某书店新进了一批图书，甲、乙两种书的进价分别为4元/本、10元/本．现购进 $m$ 本甲种书和 $n$ 本乙种书，共付款 $Q$ 元．

(1)、用含m，n的代数式表示 $Q$ ；

(2)、若共购进 $5 \times 10^{4}$ 本甲种书及 $3 \times 10^{3}$ 本乙种书，用科学记数法表示 $Q$ 的值．

查看试题解析
21. 有个填写运算符号的游戏：在“1□2□6□9”中的每个□内，填入+，﹣，×，÷中的某一个（可重复使用），然后计算结果．

(1)、计算：1+2﹣6﹣9；

(2)、若1÷2×6□9＝﹣6，请推算□内的符号；

(3)、在“1□2□6﹣9”的□内填入符号后，使计算所得数最小，直接写出这个最小数．

查看试题解析
22. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．
尝试

(1)、求前4个台阶上数的和是多少？

(2)、求第5个台阶上的数x是多少？
应用求从下到上前31个台阶上数的和．
发现试用含k（k为正整数）的式子表示出数“1”所在的台阶数．

查看试题解析
23. 嘉淇准备完成题目：化简：(x²+6x+8)-(6x+5x²+2)，发现系数“”印刷不清楚．

(1)、他把“”猜成3，请你化简：（3x²+6x+8）﹣（6x+5x²+2）；

(2)、他妈妈说：“你猜错了，我看到该题标准答案的结果是常数．”通过计算说明原题中“”是几？

查看试题解析
24. 有一电脑程序：每按一次按键，屏幕的A区就会自动加上 $a^{2}$ ，同时B区就会自动减去 $3 a$ ，且均显示化简后的结果．已知A，B两区初始显示的分别是25和－16，如图．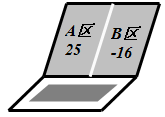

如，第一次按键后，A，B两区分别显示：

(1)、从初始状态按2次后，分别求A，B两区显示的结果；

(2)、从初始状态按4次后，计算A，B两区代数式的和，请判断这个和能为负数吗？说明理由．

查看试题解析
25. 如图，甲、乙两人（看成点）分别在数轴－3和5的位置上，沿数轴做移动游戏．每次移动游戏规则：裁判先捂住一枚硬币，再让两人猜向上一面是正是反，而后根据所猜结果进行移动．
①若都对或都错，则甲向东移动1个单位，同时乙向西移动1个单位；

②若甲对乙错，则甲向东移动4个单位，同时乙向东移动2个单位；

③若甲错乙对，则甲向西移动2个单位，同时乙向西移动4个单位．

(1)、经过第一次移动游戏，求甲的位置停留在正半轴上的概率P；

(2)、从图的位置开始，若完成了10次移动游戏，发现甲、乙每次所猜结果均为一对一错．设乙猜对n次，且他最终停留的位置对应的数为m，试用含n的代数式表示m，并求该位置距离原点 $O$ 最近时 $n$ 的值；

(3)、从图的位置开始，若进行了k次移动游戏后，甲与乙的位置相距2个单位，直接写出k的值．

查看试题解析

直角三角形三边	n²﹣1	2n	B
勾股数组Ⅰ	/	8
勾股数组Ⅱ	35	/