天津市中考数学真题汇编(近五年) 4 图形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如图, 的顶点A,B,C的坐标分别是 ,则顶点D的坐标是( )
 A、 B、 C、 D、2. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )
A、 B、 C、 D、2. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )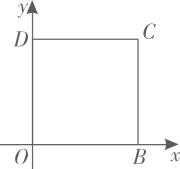 A、 B、 C、 D、3. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D , 延长 交 于点F , 则下列结论一定正确的是( )
A、 B、 C、 D、3. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D , 延长 交 于点F , 则下列结论一定正确的是( ) A、 B、 C、 D、4. 如图,四边形ABCD为菱形,A , B两点的坐标分别是(2,0),(0,1),点C , D在坐标轴上,则菱形ABCD的周长等于( )
A、 B、 C、 D、4. 如图,四边形ABCD为菱形,A , B两点的坐标分别是(2,0),(0,1),点C , D在坐标轴上,则菱形ABCD的周长等于( )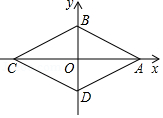 A、 B、4 C、4 D、205. 如图,将△ABC绕点C顺时针旋转得到△DEC , 使点A的对应点D恰好落在边AB上,点B的对应点为E , 连接BE , 下列结论一定正确的是( )
A、 B、4 C、4 D、205. 如图,将△ABC绕点C顺时针旋转得到△DEC , 使点A的对应点D恰好落在边AB上,点B的对应点为E , 连接BE , 下列结论一定正确的是( )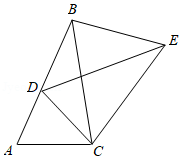 A、AC=AD B、AB⊥EB C、BC=DE D、∠A=∠EBC6. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )
A、AC=AD B、AB⊥EB C、BC=DE D、∠A=∠EBC6. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )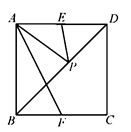 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
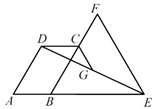
7. 如图, 的顶点C在等边 的边 上,点E在 的延长线上,G为 的中点,连接 .若 , ,则 的长为 .
 8. 如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B , 得到折痕BF , 点F在AD上,若DE=5,则GE的长为 .
8. 如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B , 得到折痕BF , 点F在AD上,若DE=5,则GE的长为 .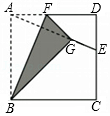 9. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A在格点上,B是小正方形边的中点,∠ABC=50°,∠BAC=30°,经过点A , B的圆的圆心在边AC上.
9. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A在格点上,B是小正方形边的中点,∠ABC=50°,∠BAC=30°,经过点A , B的圆的圆心在边AC上.
(Ⅰ)线段AB的长等于;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,画出一个点P , 使其满足∠PAC=∠PBC=∠PCB , 并简要说明点P的位置是如何找到的(不要求证明) .
10. 如图,在边长为4的等边 中, , 分别为 , 的中点, 于点 , 为 的中点,连接 ,则 的长为 . 11. 如图,正方形 的边长为4,对角线 相交于点O,点E,F分别在 的延长线上,且 ,G为 的中点,连接 ,交 于点H,连接 ,则 的长为 .
11. 如图,正方形 的边长为4,对角线 相交于点O,点E,F分别在 的延长线上,且 ,G为 的中点,连接 ,交 于点H,连接 ,则 的长为 .
 12. 如图,在每个小正方形的边长为1的网格中, 的顶点A,C均落在格点上,点B在网格线上.
12. 如图,在每个小正方形的边长为1的网格中, 的顶点A,C均落在格点上,点B在网格线上.
(Ⅰ)线段 的长等于;
(Ⅱ)以 为直径的半圆的圆心为O,在线段 上有一点P,满足 ,请用无刻度的直尺,在如图所示的网格中,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
13. 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .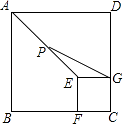 14. 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .
14. 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .
三、解答题
-
15. 已知 内接于 ,点D是 上一点.
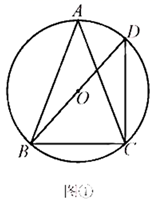

(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 // ,连接 ,过点D作 的切线,与 的延长线交于点E,求 的大小.
16. 在 中,弦 与直径 相交于点P , .
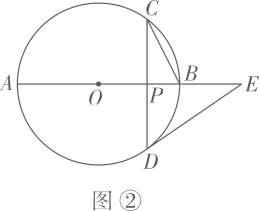 (1)、如图①,若 ,求 和 的大小;(2)、如图②,若 ,过点D作 的切线,与 的延长线相交于点E , 求 的大小.17. 已知PA , PB分别与⊙O相切于点A , B , ∠APB=80°,C为⊙O上一点.
(1)、如图①,若 ,求 和 的大小;(2)、如图②,若 ,过点D作 的切线,与 的延长线相交于点E , 求 的大小.17. 已知PA , PB分别与⊙O相切于点A , B , ∠APB=80°,C为⊙O上一点.(Ⅰ)如图①,求∠ACB的大小;
(Ⅱ)如图②,AE为⊙O的直径,AE与BC相交于点D . 若AB=AD , 求∠EAC的大小.
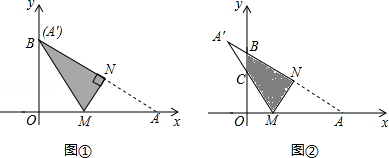
 18. 将一个直角三角形纸片ABO , 放置在平面直角坐标系中,点A( ,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O , A重合)作MN丄AB于点N , 沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m , 折叠后的△AM′N与四边形OMNB重叠部分的面积为S .
18. 将一个直角三角形纸片ABO , 放置在平面直角坐标系中,点A( ,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O , A重合)作MN丄AB于点N , 沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m , 折叠后的△AM′N与四边形OMNB重叠部分的面积为S .(Ⅰ)如图①,当点A′与顶点B重合时,求点M的坐标;
(Ⅱ)如图②,当点A′,落在第二象限时,A′M与OB相交于点C , 试用含m的式子表示S;
(Ⅲ)当S= 时,求点M的坐标(直接写出结果即可).
 19. 已知A、B、C是⊙O上的三个点.四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
19. 已知A、B、C是⊙O上的三个点.四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.(Ⅰ)如图①,求∠ADC的大小.
(Ⅱ)如图②,经过点O作CD的平行线,与AB交于点E , 与 交于点F , 连接AF , 求∠FAB的大小.

四、作图题
-
20. 如图,在每个小正方形的边长为1的网格中, 的顶点 均落在格点上,点B在网格线上,且 .
 (1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .
(1)、线段 的长等于;(2)、以 为直径的半圆与边 相交于点D , 若 分别为边 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 ,并简要说明点 的位置是如何找到的(不要求证明) .五、综合题
-
21. 如图,在每个小正方形的边长为1的网格中, 的顶点 , , 均在格点上.
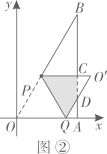
 (1)、 的大小为(度);(2)、在如图所示的网格中, 是 边上任意一点. 为中心,取旋转角等于 ,把点 逆时针旋转,点 的对应点为 .当 最短时,请用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明)22. 在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 , , 的对应点分别为 , , .
(1)、 的大小为(度);(2)、在如图所示的网格中, 是 边上任意一点. 为中心,取旋转角等于 ,把点 逆时针旋转,点 的对应点为 .当 最短时,请用无刻度的直尺,画出点 ,并简要说明点 的位置是如何找到的(不要求证明)22. 在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 .以点 为中心,顺时针旋转矩形 ,得到矩形 ,点 , , 的对应点分别为 , , .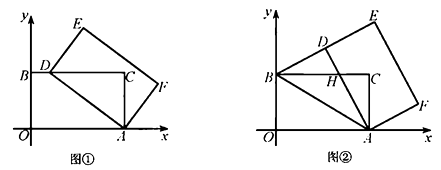 (1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .
(1)、如图①,当点 落在 边上时,求点 的坐标;(2)、如图②,当点 落在线段 上时, 与 交于点 .①求证 ;
②求点 的坐标.
(3)、记 为矩形 对角线的交点, 为 的面积,求 的取值范围(直接写出结果即可).23. 将一个直角三角形纸片ABO放置在平面直角坐标系中,点 ,点B(0,1),点O(0,0).P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A'.(1)、如图①,当点A'在第一象限,且满足A'B⊥OB时,求点A'的坐标; (2)、如图②,当P为AB中点时,求A'B的长;
(2)、如图②,当P为AB中点时,求A'B的长;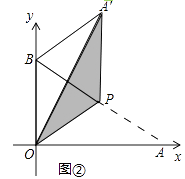 (3)、当∠BPA'=30°时,求点P的坐标(直接写出结果即可).24. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)、如图①,求∠T和∠CDB的大小;
(3)、当∠BPA'=30°时,求点P的坐标(直接写出结果即可).24. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)、如图①,求∠T和∠CDB的大小;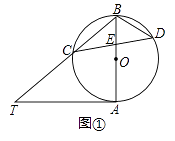 (2)、如图②,当BE=BC时,求∠CDO的大小.
(2)、如图②,当BE=BC时,求∠CDO的大小.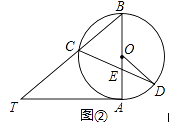 25. 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
25. 如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.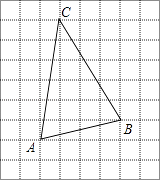 (1)、AB的长等于;(2)、在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .26. 在⊙O中,AB为直径,C为⊙O上一点.
(1)、AB的长等于;(2)、在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .26. 在⊙O中,AB为直径,C为⊙O上一点. (1)、如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;(2)、如图2,D为
(1)、如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;(2)、如图2,D为 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小. 27. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小. 27. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.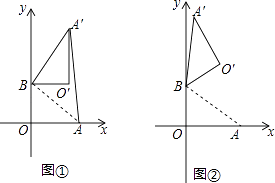 (1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)28. 如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(1)、如图①,若α=90°,求AA′的长;(2)、如图②,若α=120°,求点O′的坐标;(3)、在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)28. 如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.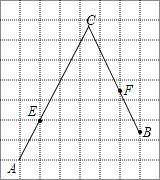 (1)、AE的长等于;(2)、若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .29. 将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点B在第一象限, , ,点P在边 上(点P不与点 重合).
(1)、AE的长等于;(2)、若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .29. 将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点B在第一象限, , ,点P在边 上(点P不与点 重合).
 (1)、如图①,当 时,求点P的坐标;(2)、折叠该纸片,使折痕所在的直线经过点P , 并与x轴的正半轴相交于点Q , 且 ,点O的对应点为 ,设 .
(1)、如图①,当 时,求点P的坐标;(2)、折叠该纸片,使折痕所在的直线经过点P , 并与x轴的正半轴相交于点Q , 且 ,点O的对应点为 ,设 .①如图②,若折叠后 与 重叠部分为四边形, 分别与边 相交于点 ,试用含有t的式子表示 的长,并直接写出t的取值范围;
②若折叠后 与 重叠部分的面积为S , 当 时,求S的取值范围(直接写出结果即可).
30. 已知 是 的直径,弦 与 相交, . (1)、如图①,若 为
(1)、如图①,若 为 的中点,求 和 的大小;
的中点,求 和 的大小;
(2)、如图②,过点 作 的切线,与 的延长线交于点 ,若 ,求 的大小.
-