天津市中考数学真题汇编（近五年） 3 函数

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 若点A（﹣1，y₁），B（1，y₂），C（3，y₃）在反比例函数 $y = - \frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₃＜y₁ C、y₃＜y₂＜y₁ D、y₂＜y₁＜y₃

查看试题解析
2. 已知抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $a \neq 0$ ）经过点 $(- 1 ， - 1) ， (0 ， 1)$ ，当 $x = - 2$ 时，与其对应的函数值 $y > 1$ ．有下列结论：① $a b c > 0$ ；②关于x的方程 $a x^{2} + b x + c - 3 = 0$ 有两个不等的实数根；③ $a + b + c > 7$ ．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 若点 $A (- 5 ， y_{1}) ， B (1 ， y_{2}) ， C (5 ， y_{3})$ 都在反比例函数 $y = - \frac{5}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
4. 如图，四边形 $O B C D$ 是正方形，O ， D两点的坐标分别是 $(0 ， 0)$ ， $(0 ， 6)$ ，点C在第一象限，则点C的坐标是（）

A、 $(6 ， 3)$ B、 $(3 ， 6)$ C、 $(0 ， 6)$ D、 $(6 ， 6)$

查看试题解析
5. 若点 $A (x_{1} ， - 5) ， B (x_{2} ， 2) ， C (x_{3} ， 5)$ 都在反比例函数 $y = \frac{10}{x}$ 的图象上，则 $x_{1} ， x_{2} ， x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{3} < x_{1}$ C、 $x_{1} < x_{3} < x_{2}$ D、 $x_{3} < x_{1} < x_{2}$

查看试题解析
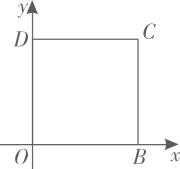6. 若点 $A (x_{1} ， - 6)$ ， $B (x_{2} ， - 2)$ ， $C (x_{3} ， 2)$ 在反比例函数 $y = \frac{12}{x}$ 的图像上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{1} < x_{3}$ C、 $x_{2} < x_{3} < x_{1}$ D、 $x_{3} < x_{2} < x_{1}$

查看试题解析
7. 已知二次函数y=（x﹣h）²+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）

A、1或﹣5 B、﹣1或5 C、1或﹣3 D、1或3

查看试题解析
8. 若点A（﹣5，y₁），B（﹣3，y₂），C（2，y₃）在反比例函数y= $\frac{3}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₃＜y₂ B、y₁＜y₂＜y₃ C、y₃＜y₂＜y₁ D、y₂＜y₁＜y₃

查看试题解析
9. 已知抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 为常数， $a \neq 0$ ）经过点 $(- 1 ， 0)$ . ， $(0 ， 3)$ ，其对称轴在 $y$ 轴右侧，有下列结论：①抛物线经过点 $(1 ， 0)$ ；②方程 $a x^{2} + b x + c = 2$ 有两个不相等的实数根；③ $- 3 < a + b < 3$ .，正确结论的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 二次函数y＝ax²+bx+c（a ， b ， c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：

x

…

﹣2

﹣1

0

1

2

…

y＝ax²+bx+c

…

t

m

﹣2

﹣2

n

…

且当x＝﹣ $\frac{1}{2}$ 时，与其对应的函数值y＞0．有下列结论：

①abc＞0；②﹣2和3是关于x的方程ax²+bx+c＝t的两个根；③0＜m+n＜ $\frac{20}{3}$ ．

其中，符合题意结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
11. 已知抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $a \neq 0 ， c > 1$ ）经过点 $(2 ， 0)$ ，其对称轴是直线 $x = \frac{1}{2}$ ．有下列结论：
① $a b c > 0$ ；②关于x的方程 $a x^{2} + b x + c = a$ 有两个不等的实数根；③ $a < - \frac{1}{2}$ ．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
12. 已知抛物线y=x²﹣4x+3与x轴相交于点A，B（点A在点B左侧），顶点为M．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（）

A、y=x²+2x+1 B、y=x²+2x﹣1 C、y=x²﹣2x+1 D、y=x²﹣2x﹣1

查看试题解析
13.
如图，在直角坐标系xOy中，点A，B分别在x轴和y轴， $\frac{O A}{O B} = \frac{3}{4}$ ． ∠AOB的角平分线与OA的垂直平分线交于点C，与AB交于点D，反比例函数y= $\frac{k}{x}$ 的图象过点C．当以CD为边的正方形的面积为 $\frac{2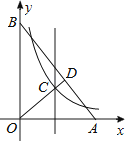}{7}$ 时，k的值是（　　）

A、2 B、3 C、5 D、7

查看试题解析

二、填空题

14. 将直线 $y = - 6 x$ 向下平移2个单位长度，平移后直线的解析式为．

查看试题解析
15. 直线y＝2x﹣1与x轴的交点坐标为．

查看试题解析
16. 将直线 $y = x$ 向上平移2个单位长度，平移后直线的解析式为．

查看试题解析
17. 若正比例函数y=kx（k是常数，k≠0）的图象经过第二、四象限，则k的值可以是（写出一个即可）．

查看试题解析
18. 将直线 $y = - 2 x$ 向上平移1个单位长度，平移后直线的解析式为．

查看试题解析
19. 若一次函数y=﹣2x+b（b为常数）的图象经过第二、三、四象限，则b的值可以是（写出一个即可）．

查看试题解析

三、解答题

20. 已知抛物线 $y = a x^{2} - 2 a x + c$ （a，c为常数， $a \neq 0$ ）经过点 $C (0 ， - 1)$ ，顶点为D．
（Ⅰ）当 $a = 1$ 时，求该抛物线的顶点坐标；

（Ⅱ）当 $a > 0$ 时，点 $E (0 ， 1 + a)$ ，若 $D E = 2 \sqrt{2} D C$ ，求该抛物线的解析式；

（Ⅲ）当 $a < - 1$ 时，点 $F (0 ， 1 - a)$ ，过点C作直线l平行于x轴， $M (m ， 0)$ 是x轴上的动点， $N (m + 3 ， - 1)$ 是直线l上的动点．当a为何值时， $F M + D N$ 的最小值为 $2 \sqrt{10}$ ，并求此时点M，N的坐标．

查看试题解析
21. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．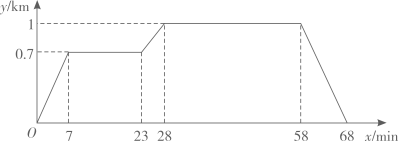

已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍 $0 . 7km$ ，图书馆离宿舍 $1km$ ．周末，小亮从宿舍出发，匀速走了 $7min$ 到食堂；在食堂停留 $16min$ 吃早餐后，匀速走了 $5min$ 到图书馆；在图书馆停留 $30min$ 借书后，匀速走了 $10min$ 返回宿舍，给出的图象反映了这个过程中小亮离宿舍的距离 $y km$ 与离开宿舍的时间 $x min$ 之间的对应关系．

请根据相关信息，解答下列问题：

(1)、填表：

离开宿舍的时间/ $min$

2

5

20

23

30

离宿舍的距离/ $km$

0.2

0.7

(2)、填空：
①食堂到图书馆的距离为 $km$ ．

②小亮从食堂到图书馆的速度为 $km/min$ ．

③小亮从图书馆返回宿舍的速度为 $km/min$ ．

④当小亮离宿舍的距离为 $0 . 6km$ 时，他离开宿舍的时间为 $min$ ．

(3)、当 $0 \leq x \leq 28$ 时，请直接写出y关于x的函数解析式．

查看试题解析
22. 在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D ， E ， C分别在OA ， AB ， OB上，OD＝2．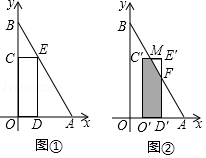

（Ⅰ）如图①，求点E的坐标；

（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C ， O ， D ， E的对应点分别为C′，O′，D′，E′．设OO′＝t ，矩形C′O′D′E′与△ABO重叠部分的面积为S ．

①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M ， F ，试用含有t的式子表示S ，并直接写出t的取值范围；

②当 $\sqrt{3}$ ≤S≤5 $\sqrt{3}$ 时，求t的取值范围（直接写出结果即可）．

查看试题解析
23. 已知二次函数y=x²+bx+c（b ， c为常数）．
（Ⅰ）当b=2，c=﹣3时，求二次函数的最小值；

（Ⅱ）当c=5时，若在函数值y=l的怙况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；

（Ⅲ）当c=b²时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．

查看试题解析

四、综合题

24. 在平面直角坐标系中，点 $O (0 ， 0)$ ，点 $A (1 ， 0)$ .已知抛物线 $y = x^{2} + m x - 2 m$ （ $m$ 是常数），顶点为 $P$ .

(1)、当抛物线经过点 $A$ 时，求顶点 $P$ 的坐标；

(2)、若点 $P$ 在 $x$ 轴下方，当 $∠ A O P = 45 °$ 时，求抛物线的解析式；

(3)、无论 $m$ 取何值，该抛物线都经过定点 $H$ .当 $∠ A H P = 45 °$ 时，求抛物线的解析式.

查看试题解析
25. 某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.
设小明计划今年夏季游泳次数为 $x$ （ $x$ 为正整数）.

(1)、根据题意，填写下表：
游泳次数
10
15
20
…
$x$
方式一的总费用（元）
150
175
…
方式二的总费用（元）
90
135
…

(2)、若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？

(3)、当 $x > 20$ 时，小明选择哪种付费方式更合算？并说明理由.

查看试题解析
26. 已知抛物线y=x²+bx﹣3（b是常数）经过点A（﹣1，0）．

(1)、求该抛物线的解析式和顶点坐标；

(2)、P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．
①当点P'落在该抛物线上时，求m的值；
②当点P'落在第二象限内，P'A²取得最小值时，求m的值．

查看试题解析
27. 公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台、租车费用为400元，每辆乙种货车一次最多运送机器30台、租车费用为280元

(1)、设租用甲种货车x辆（x为非负整数），试填写表格．
表一：
租用甲种货车的数量/辆
3
7
x
租用的甲种货车最多运送机器的数量/台
135
租用的乙种货车最多运送机器的数量/台
150
表二：
租用甲种货车的数量/辆
3
7
x
租用甲种货车的费用/元
2800
租用乙种货车的费用/元
280

(2)、给出能完成此项运送任务的最节省费用的租车方案，并说明理由．

查看试题解析
28. 已知点 $A (1 ， 0)$ 是抛物线 $y = a x^{2} + b x + m$ （ $a ， b ， m$ 为常数， $a \neq 0 ， m < 0$ ）与x轴的一个交点．

(1)、当 $a = 1 ， m = - 3$ 时，求该抛物线的顶点坐标；

(2)、若抛物线与x轴的另一个交点为 $M (m ， 0)$ ，与y轴的交点为C ，过点C作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点， $E F = 2 \sqrt{2}$ ．
①当点E落在抛物线上（不与点C重合），且 $A E = E F$ 时，求点F的坐标；

②取 $E F$ 的中点N ，当m为何值时， $M N$ 的最小值是 $\frac{\sqrt{2}}{2}$ ？

查看试题解析
29. 用A4纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．
设在同一家复印店一次复印文件的页数为x（x为非负整数）．

(1)、根据题意，填写下表：
一次复印页数（页）
5
10
20
30
…
甲复印店收费（元）
0.5
2
…
乙复印店收费（元）
0.6
2.4
…

(2)、设在甲复印店复印收费y₁元，在乙复印店复印收费y₂元，分别写出y₁ ， y₂关于x的函数关系式；

(3)、当x＞70时，顾客在哪家复印店复印花费少？请说明理由．

查看试题解析

30. 甲、乙两个批发店销售同一种苹果，在甲批发店，不论一次购买数量是多少，价格均为6元/kg ．在乙批发店，一次购买数量不超过50kg时，价格为7元/kg；一次购买数量超过50kg时，其中有50kg的价格仍为7元/kg ，超过50kg部分的价格为5元/kg ．设小王在同一个批发店一次购买苹果的数量为xkg（x＞0）．

(1)、根据题意填表：

一次购买数量/kg	30	50	150	…
甲批发店花费/元		300		…
乙批发店花费/元		350		…

(2)、设在甲批发店花费y₁元，在乙批发店花费y₂元，分别求y₁ ， y₂关于x的函数解析式；

(3)、根据题意填空：

①若小王在甲批发店和在乙批发店一次购买苹果的数量相同，且花费相同，则他在同一个批发店一次购买苹果的数量为kg；

②若小王在同一个批发店一次购买苹果的数量为120kg ，则他在甲、乙两个批发店中的批发店购买花费少；

③若小王在同一个批发店一次购买苹果花费了360元，则他在甲、乙两个批发店中的批发店购买数量多．

查看试题解析

31. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．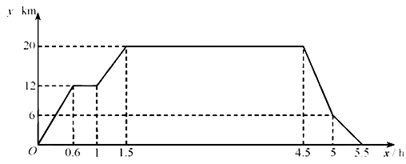

已知学校、书店、陈列馆依次在同一条直线上，书店离学校 $12km$ ，陈列馆离学校 $20km$ ．李华从学校出发，匀速骑行 $0 .6h$ 到达书店；在书店停留 $0 .4h$ 后，匀速骑行 $0 .5h$ 到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行 $0 .5h$ 后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离 $y km$ 与离开学校的时间 $x h$ 之间的对应关系．

请根据相关信息，解答下列问题：

(1)、填表

离开学校的时间/ $h$

$0.1$

$0.5$

$0.8$

$1$

$3$

离学校的距离/ $km$

2

12

(2)、填空：
①书店到陈列馆的距离为 $km$ ；

②李华在陈列馆参观学的时间为h；

③李华从陈列馆回学校途中，减速前的骑行速度为 $km/h$ ；

④当李华离学校的距离为 $4km$ 时，他离开学校的时间为h．

(3)、当 $0 \leq x \leq 1.5$ 时，请直接写出y关于x的函数解析式．

查看试题解析

离开宿舍的时间/ $min$	2	5	20	23	30
离宿舍的距离/ $km$	0.2		0.7

游泳次数	10	15	20	…	$x$
方式一的总费用（元）	150	175		…
方式二的总费用（元）	90	135		…

租用甲种货车的数量/辆	3	7	x
租用的甲种货车最多运送机器的数量/台	135
租用的乙种货车最多运送机器的数量/台	150

租用甲种货车的数量/辆	3	7	x
租用甲种货车的费用/元		2800
租用乙种货车的费用/元		280

一次复印页数（页）	5	10	20	30	…
甲复印店收费（元）	0.5		2		…
乙复印店收费（元）	0.6		2.4		…

离开学校的时间/ $h$	$0.1$	$0.5$	$0.8$	$1$	$3$
离学校的距离/ $km$	2			12

x	…	﹣2	﹣1	0	1	2	…
y＝ax²+bx+c	…	t	m	﹣2	﹣2	n	…