北京市中考数学真题汇编(近五年)7 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、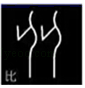 2.
2.如图是某个几何体的三视图,该几何体是( )
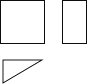 A、圆锥 B、三棱锥 C、圆柱 D、三棱柱3. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、
A、圆锥 B、三棱锥 C、圆柱 D、三棱柱3. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、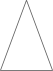 B、
B、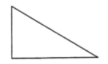 C、
C、 D、
D、 4. 如图是某几何体的三视图,该几何体是( )
4. 如图是某几何体的三视图,该几何体是( )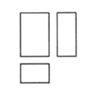 A、圆柱 B、圆锥 C、三棱锥 D、长方体5. 下列倡导节约的图案中,是轴对称图形的是( )A、
A、圆柱 B、圆锥 C、三棱锥 D、长方体5. 下列倡导节约的图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
6. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
7. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
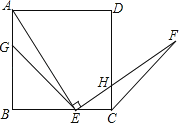 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 在平面直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的纵坐标分别为 ,则 的值为 .9. 在如图所示的几何体中,其三视图中有矩形的是.(写出所有正确答案的序号)
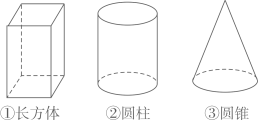 10. 如图,在矩形 中, 是边 的中点,连接 交对角线 于点 ,若 , ,则 的长为 .
10. 如图,在矩形 中, 是边 的中点,连接 交对角线 于点 ,若 , ,则 的长为 .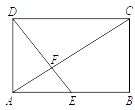 11. 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一中由△OCD得到△AOB的过程: .
11. 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一中由△OCD得到△AOB的过程: . 12. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为m.
12. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为m. 13. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .
13. 如图,在Rt△ABC中,∠A=90°, ∠B=30°,BC= +1,点E、F分别是BC、AC边上的动点,沿EF所在直线折叠∠C,使点C的对应点C′始终落在边AB上,若△BEC′是直角三角形时,则BC′的长为 .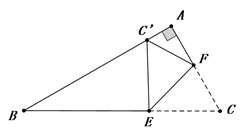
三、综合题
-
14. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位长度得到.(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.15. 如图, 是 的外接圆, 是 的直径, 于点 .
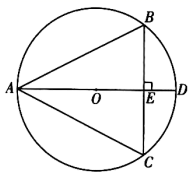 (1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.16. 如图,在 中, 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 .
(1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.16. 如图,在 中, 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 .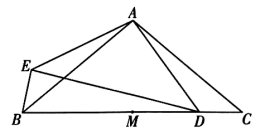 (1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.17. 如图,在边上为1个单位长度的小正方形网格中:
(1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.17. 如图,在边上为1个单位长度的小正方形网格中: (1)、画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1 .(2)、以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 请在网格中画出△A2B2C2 .(3)、求△CC1C2的面积.18. 小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.
(1)、画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1 .(2)、以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 请在网格中画出△A2B2C2 .(3)、求△CC1C2的面积.18. 小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm. (1)、求∠CAO′的度数(2)、显示屏的顶部B′比原来升高了多少?(3)、如图4,垫入散热架后,要使显示屏O′B与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
(1)、求∠CAO′的度数(2)、显示屏的顶部B′比原来升高了多少?(3)、如图4,垫入散热架后,要使显示屏O′B与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?