北京市中考数学真题汇编(近五年)6 图形的性质---圆
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )
 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD二、填空题
-
2. 如图, 是 的切线, 是切点.若 ,则 .
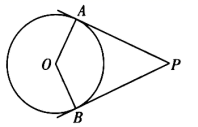 3. 如图,点 , , , 在 上, , , ,则 .
3. 如图,点 , , , 在 上, , , ,则 . 4. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= .
4. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= .
三、综合题
-
5. 如图, 是 的外接圆, 是 的直径, 于点 .
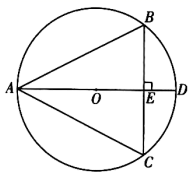 (1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.6. 在平面直角坐标系 中, 的半径为1,对于点 和线段 ,给出如下定义:若将线段 绕点 旋转可以得到 的弦 ( 分别是 的对应点),则称线段 是 的以点 为中心的“关联线段”.
(1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.6. 在平面直角坐标系 中, 的半径为1,对于点 和线段 ,给出如下定义:若将线段 绕点 旋转可以得到 的弦 ( 分别是 的对应点),则称线段 是 的以点 为中心的“关联线段”.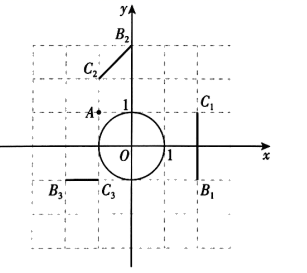 (1)、如图,点 的横、纵坐标都是整数.在线段 中, 的以点 为中心的“关联线段”是;(2)、 是边长为1的等边三角形,点 ,其中 .若 是 的以点 为中心的“关联线段”,求 的值;(3)、在 中, .若 是 的以点 为中心的“关联线段”,直接写出 的最小值和最大值,以及相应的 长.7. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)、如图,点 的横、纵坐标都是整数.在线段 中, 的以点 为中心的“关联线段”是;(2)、 是边长为1的等边三角形,点 ,其中 .若 是 的以点 为中心的“关联线段”,求 的值;(3)、在 中, .若 是 的以点 为中心的“关联线段”,直接写出 的最小值和最大值,以及相应的 长.7. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.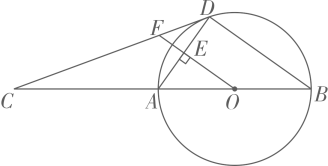 (1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.8. 在平面直角坐标系 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦 ( 分别为点A,B的对应点),线段 长度的最小值称为线段AB到⊙O的“平移距离”.
(1)、求证:∠ADC=∠AOF;(2)、若sinC= ,BD=8,求EF的长.8. 在平面直角坐标系 中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦 ( 分别为点A,B的对应点),线段 长度的最小值称为线段AB到⊙O的“平移距离”.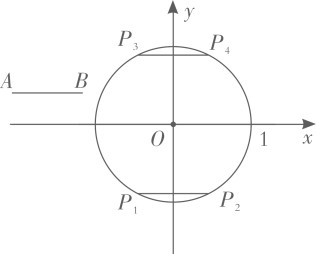 (1)、如图,平移线段AB到⊙O的长度为1的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”;(2)、若点A,B都在直线 上,记线段AB到⊙O的“平移距离”为 ,求 的最小值;(3)、若点A的坐标为 ,记线段AB到⊙O的“平移距离”为 ,直接写出 的取值范围.9. 如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , .
(1)、如图,平移线段AB到⊙O的长度为1的弦 和 ,则这两条弦的位置关系是;在点 中,连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”;(2)、若点A,B都在直线 上,记线段AB到⊙O的“平移距离”为 ,求 的最小值;(3)、若点A的坐标为 ,记线段AB到⊙O的“平移距离”为 ,直接写出 的取值范围.9. 如图, 是 的直径,过 外一点 作 的两条切线 , ,切点分别为 , ,连接 , . (1)、求证: ;
(1)、求证: ;
(2)、连接 , ,若 , , ,求 的长.10. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
5
6
y/cm
0
2.0
2.3
2.1
0.9
0
(说明:补全表格时相关数值保留一位小数)
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象. (3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.11. 在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.11. 在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)、当⊙O的半径为2时,①在点P1( ,0),P2( , ),P3( ,0)中,⊙O的关联点是 .
②点P在直线y=﹣x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
(2)、⊙C的圆心在x轴上,半径为2,直线y=﹣x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
12. 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. (1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.
(1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.
-

