北京市中考数学真题汇编(近五年)5 图形的性质----四边形和多边形
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 内角和为540°的多边形是( )A、
 B、
B、 C、
C、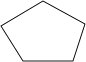 D、
D、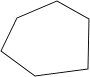 2. 下列多边形中,内角和最大的是( )A、
2. 下列多边形中,内角和最大的是( )A、 B、
B、 C、
C、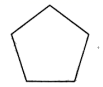 D、
D、 3. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、4. 正五边形的外角和为( )A、180° B、360° C、540° D、720°5. 正十边形的外角和为( )A、180° B、360° C、720° D、1440°6. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、187. 如图是某个几何体的展开图,该几何体是( )
3. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、4. 正五边形的外角和为( )A、180° B、360° C、540° D、720°5. 正十边形的外角和为( )A、180° B、360° C、720° D、1440°6. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、187. 如图是某个几何体的展开图,该几何体是( )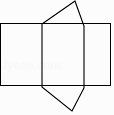 A、三棱柱 B、圆锥 C、四棱柱 D、圆柱8. 下列几何体中,是圆柱的为( )A、
A、三棱柱 B、圆锥 C、四棱柱 D、圆柱8. 下列几何体中,是圆柱的为( )A、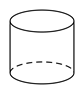 B、
B、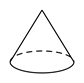 C、
C、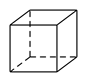 D、
D、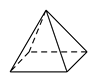
二、填空题
-
9. 如图,在矩形 中,点 分别在 上, .只需添加一个条件即可证明四边形 是菱形,这个条件可以是(写出一个即可).
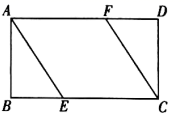 10. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .
10. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .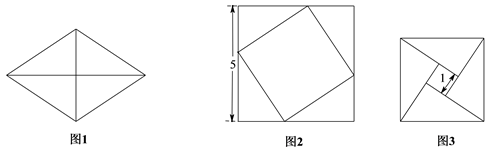
三、解答题
-
11. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.

证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
四、综合题
-
12. 如图,在 中, 为 的中点,点 在 上,以点 为中心,将线段 顺时针旋转 得到线段 ,连接 .
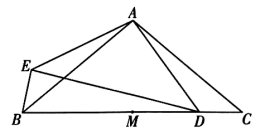 (1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.13. 如图,在四边形 中, ,点 在 上, ,垂足为 .
(1)、比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)、过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.13. 如图,在四边形 中, ,点 在 上, ,垂足为 . (1)、求证:四边形 是平行四边形;(2)、若 平分 ,求 和 的长.14. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)、求证:四边形 是平行四边形;(2)、若 平分 ,求 和 的长.14. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF. (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.15. 下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.15. 下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线及直线外一点 .

求作: ,使得 .
作法:如图,

①在直线上取一点 ,作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
②在直线上取一点 (不与点 重合),作射线 ,以点 为圆心, 长为半径画弧,交 的延长线于点 ;
③作直线 .
所以直线 就是所求作的直线.
根据小东设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵ , ,
∴ ()(填推理的依据).
16. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
17. 如图,在正方形 中, 是边 上的一动点(不与点 , 重合),连接 ,点 关于直线 的对称点为 ,连接 并延长交 于点 ,连接 ,过点 作 交 的延长线于点 ,连接 .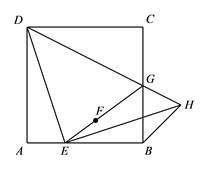 (1)、求证: ;
(1)、求证: ;
(2)、用等式表示线段 与 的数量关系,并证明.18. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.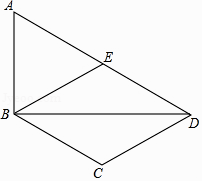 (1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.19. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.19. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图. (1)、已知点A的坐标为(1,0),
(1)、已知点A的坐标为(1,0),①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)、⊙O的半径为 ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.20. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN. (1)、求证:BM=MN;(2)、∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
(1)、求证:BM=MN;(2)、∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
-