北京市中考数学真题汇编（近五年）4 图形的性质----三角形

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图所示，点P到直线l的距离是（）

A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度

查看试题解析
2. 如图，点 $O$ 在直线 $A B$ 上， $O C ⊥ O D$ ．若 $∠ A O C = 120 °$ ，则 $∠ B O D$ 的大小为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
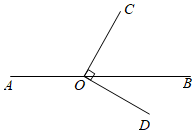3. 如图，AB和CD相交于点O，则下列结论正确的是（）

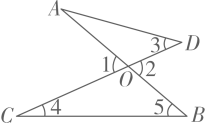A、∠1=∠2 B、∠2=∠3 C、∠1＞∠4+∠5 D、∠2＜∠5

查看试题解析

二、填空题

4. 在 $△$ ABC中，AB=AC，点D在BC上（不与点B，C重合）．只需添加一个条件即可证明 $△$ ABD≌ $△$ ACD，这个条件可以是（写出一个即可）

查看试题解析
5. 如图所示的网格是正方形网格，A，B，C，D是网格交点，则 $△$ ABC的面积与 $△$ ABD的面积的大小关系为： $S_{△ A B C}$ $S_{△ A B D}$ （填“＞”，“＝”或“＜”）

查看试题解析
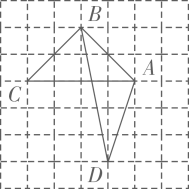6. 如图所示的网格是正方形网格，则 $∠ P A B ＋ ∠ P B A$ ＝°（点A，B，P是网格线交点）.

查看试题解析
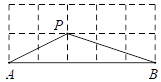7.
下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：
已知：直线l和l外一点P．（如图1）
求作：直线l的垂线，使它经过点P．
作法：如图2（1）在直线l上任取两点A，B；（2）分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；（3）作直线PQ．
所以直线PQ就是所求的垂线．
请回答：该作图的依据是

查看试题解析
8. 如图，已知△ABC，通过测量、计算得△ABC的面积约为cm².（结果保留一位小数）

查看试题解析
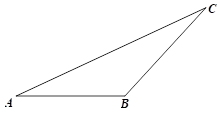9. 如图，在△ABC中，M、N分别为AC，BC的中点．若S_△CMN=1，则S_{四边形ABNM}= ．

查看试题解析
10. 如图，在Rt△ABC中，∠ACB=90°，点D，E分别是AB，AC的中点，点F是AD的中点．若AB=8，则EF= ．

查看试题解析

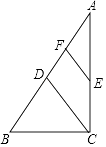
三、解答题

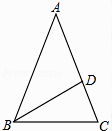
11. 如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D．
求证：AD=BC．

查看试题解析

四、作图题

12. 已知：如图， $△$ ABC为锐角三角形，AB=BC，CD∥AB．
求作：线段BP，使得点P在直线CD上，且∠ABP= $\frac{1}{2} ∠ B A C$ ．

作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）

(2)、完成下面的证明．
证明：∵CD∥AB，

∴∠ABP= ．

∵AB=AC，

∴点B在⊙A上．

又∵∠BPC= $\frac{1}{2}$ ∠BAC（）（填推理依据）

∴∠ABP= $\frac{1}{2}$ ∠BAC

查看试题解析

五、综合题

13. 《淮南子･天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点 $A$ 处立一根杆，在地面上沿着杆的影子的方向取一点 $B$ ，使 $B ， A$ 两点间的距离为10步（步是古代的一种长度单位），在点 $B$ 处立一根杆；日落时，在地面上沿着点 $B$ 处的杆的影子的方向取一点 $C$ ，使 $C ， B$ 两点间的距离为10步，在点 $C$ 处立一根杆．取 $C A$ 的中点 $D$ ，那么直线 $D B$ 表示的方向为东西方向．

(1)、上述方法中，杆在地面上的影子所在直线及点 $A ， B ， C$ 的位置如图所示．使用直尺和圆规，在图中作 $C A$ 的中点 $D$ （保留作图痕迹）；

(2)、在如图中，确定了直线 $D B$ 表示的方向为东西方向．根据南北方向与东西方向互相垂直，可以判断直线 $C A$ 表示的方向为南北方向，完成如下证明．
证明：在 $△ A B C$ 中， $B A =$ ▲ ， $D$ 是 $C A$ 的中点，

$∴ C A ⊥ D B$ ▲ （填推理的依据）．

∵直线 $D B$ 表示的方向为东西方向，

∴直线 $C A$ 表示的方向为南北方向．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C ， ∠ B A C = α ， M$ 为 $B C$ 的中点，点 $D$ 在 $M C$ 上，以点 $A$ 为中心，将线段 $A D$ 顺时针旋转 $α$ 得到线段 $A E$ ，连接 $B E ， D E$ ．

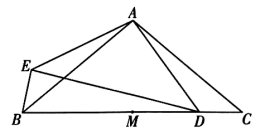(1)、比较 $∠ B A E$ 与 $∠ C A D$ 的大小；用等式表示线段 $B E ， B M ， M D$ 之间的数量关系，并证明；

(2)、过点 $M$ 作 $A B$ 的垂线，交 $D E$ 于点 $N$ ，用等式表示线段 $N E$ 与 $N D$ 的数量关系，并证明．

查看试题解析
15. 在 $△ A B C$ 中，∠C=90°，AC＞BC，D是AB的中点．E为直线上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．

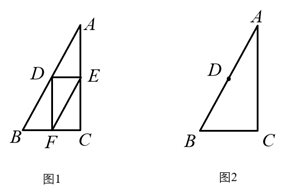(1)、如图1，当E是线段AC的中点时，设 $A E = a ， B F = b$ ，求EF的长（用含 $a ， b$ 的式子表示）；

(2)、当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．

查看试题解析
16. 已知 $∠ A O B = 30 °$ ，H为射线OA上一定点， $O H = \sqrt{3} + 1$ ，P为射线OB上一点，M为线段OH上一动点，连接PM，满足 $∠ O M P$ 为钝角，以点P为中心，将线段PM顺时针旋转 $150 °$ ，得到线段PN，连接ON．

(1)、依题意补全图1；

(2)、求证： $∠ O M P = ∠ O P N$ ；

(3)、点M关于点H的对称点为Q，连接QP．写出一个OP的值，使得对于任意的点M总有ON=QP，并证明．

查看试题解析
17. 在△ABC中， $D$ ， $E$ 分别是 $△ A B C$ 两边的中点，如果 $\overset{⌢}{D E}$ 上的所有点都在△ABC的内部或边上，则称 $\overset{⌢}{D E}$ 为△ABC的中内弧．例如，下图中 $\overset{⌢}{D E}$ 是△ABC的一条中内弧．

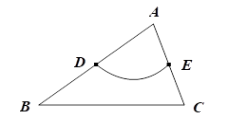(1)、如图，在Rt△ABC中， $A B = A C = 2 \sqrt{2} ， D ， E$ 分别是 $A B ， A C$ 的中点．画出△ABC的最长的中内弧 $\overset{⌢}{D E}$ ，并直接写出此时 $\overset{⌢}{D E}$ 的长；

(2)、在平面直角坐标系中，已知点 $A (0 ， 2) ， B (0 ， 0) ， C (4 t ， 0) (t > 0)$ ，在△ABC中， $D ， E$ 分别是 $A B ， A C$ 的中点．
①若 $t = \frac{1}{2}$ ，求△ABC的中内弧 $\overset{⌢}{D E}$ 所在圆的圆心 $P$ 的纵坐标的取值范围；

②若在△ABC中存在一条中内弧 $\overset{⌢}{D E}$ ，使得 $\overset{⌢}{D E}$ 所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．

查看试题解析
18. 在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G， $∠ A B C$ 的平分线交图形G于点D，连接AD，CD．

(1)、求证：AD=CD；

(2)、过点D作DE $⊥$ BA，垂足为E，作DF $⊥$ BC，垂足为F，延长DF交图形G于点M，连接CM．若AD=CM，求直线DE与图形G的公共点个数．

查看试题解析
19. 在等腰直角△ABC中，∠ACB=90°，P是线段BC上一动点（与点B、C不重合），连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M．

(1)、若∠PAC=α，求∠AMQ的大小（用含α的式子表示）．

(2)、用等式表示线段MB与PQ之间的数量关系，并证明．

查看试题解析
20.
在等边△ABC中，

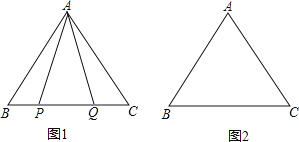(1)、如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；

(2)、点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．

查看试题解析