北京市中考数学真题汇编（近五年）3 函数

试卷更新日期：2021-08-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为 $x$ 轴、 $y$ 轴的正方向建立平面直角坐标系，有如下四个结论：

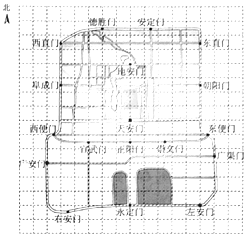
①当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（ $- 6$ ， $- 3$ ）时，表示左安门的点的坐标为（5， $- 6$ ）；②当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（ $- 12$ ， $- 6$ ）时，表示左安门的点的坐标为（10， $- 12$ ）；③当表示天安门的点的坐标为（1，1），表示广安门的点的坐标为（ $- 11$ ， $- 5$ ）时，表示左安门的点的坐标为（ $11$ ， $- 11$ ）；④当表示天安门的点的坐标为（ $1.5$ ， $1.5$ ），表示广安门的点的坐标为（ $- 16.5$ ， $- 7.5$ ）时，表示左安门的点的坐标为（ $16.5$ ， $- 16.5$ ）．上述结论中，所有正确结论的序号是（）

A、①②③ B、②③④ C、①④ D、①②③④

查看试题解析
2. 如图，用绳子围成周长为 $10m$ 的矩形，记矩形的一边长为 $x m$ ，它的邻边长为 $y m$ ，矩形的面积为 $S m^{2}$ ．当 $x$ 在一定范围内变化时， $y$ 和 $S$ 都随 $x$ 的变化而变化，则 $y$ 与 $x ， S$ 与 $x$ 满足的函数关系分别是（）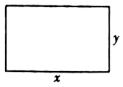

A、一次函数关系，二次函数关系 B、反比例函数关系，二次函数关系 C、一次函数关系，反比例函数关系 D、反比例函数关系，一次函数关系

查看试题解析
3. 有一个装有水的容器，如图所示．容器内的水面高度是10cm，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的函数关系是（）

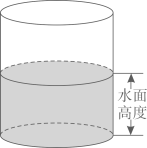A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系

查看试题解析
4. 跳台滑雪是冬季奥运会比赛项目之一．运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度 $y$ （单位： $m$ ）与水平距离 $x$ （单位： $m$ ）近似满足函数关系 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）．下图记录了某运动员起跳后的 $x$ 与 $y$ 的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（）

A、 $10 m$ B、 $15 m$ C、 $20 m$ D、 $22.5 m$

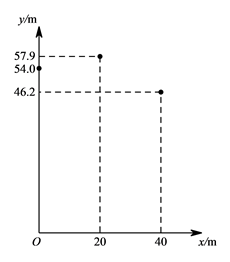查看试题解析
5. 小苏和小林在如图1所示的跑道上进行4×50米折返跑．在整个过程中，跑步者距起跑线的距离y（单位：m）与跑步时间t（单位：s）的对应关系如图2所示．下列叙述正确的是（）

A、两人从起跑线同时出发，同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏前15s跑过的路程大于小林前15s跑过的路程 D、小林在跑最后100m的过程中，与小苏相遇2次

查看试题解析
6.
如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（﹣4，2），点B的坐标为（2，﹣4），则坐标原点为（　　）

A、O₁ B、O₂ C、O₃ D、O₄

查看试题解析

二、填空题

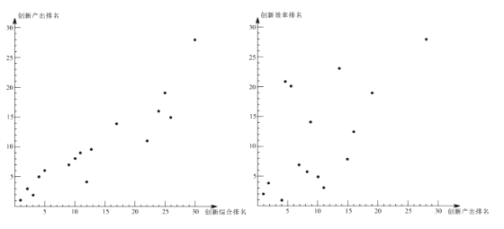
7. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (1 ， 2)$ 和点 $B (- 1 ， m)$ ，则 $m$ 的值为．

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，直线 $y = x$ 与双曲线 $y = \frac{m}{x}$ 交于A，B两点．若点A，B的纵坐标分别为 $y_{1} ， y_{2}$ ，则 $y_{1} + y_{2}$ 的值为．

查看试题解析
9. 在平面直角坐标系 $x O y$ 中，点 $A$ $(a ， b)$ $(a > 0 ， b > 0)$ 在双曲线 $y = \frac{k_{1}}{x}$ 上．点 $A$ 关于 $x$ 轴的对称点 $B$ 在双曲线 $y = \frac{k_{2}}{x}$ 上，则 $k_{1} + k_{2}$ 的值为.

查看试题解析
10. 2017年，部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示，中国创新综合排名全球第22，创新效率排名全球第．

查看试题解析

三、综合题

11. 在平面直角坐标系 $x O y$ 中，点 $(1 ， m)$ 和点 $(3 ， n)$ 在抛物线 $y = a x^{2} + b x (a > 0)$ 上．

(1)、若 $m = 3 ， n = 15$ ，求该抛物线的对称轴；

(2)、已知点 $(- 1 ， y_{1}) ， (2 ， y_{2}) ， (4 ， y_{3})$ 在该抛物线上．若 $m n < 0$ ，比较 $y_{1} ， y_{2} ， y_{3}$ 的大小，并说明理由．

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象 $G$ 经过点 $A$ （4，1），直线 $l ∶ y = \frac{1}{4} x + b$ 与图象 $G$ 交于点 $B$ ，与 $y$ 轴交于点 $C$ ．

(1)、求 $k$ 的值；

(2)、横、纵坐标都是整数的点叫做整点．记图象 $G$ 在点 $A$ ， $B$ 之间的部分与线段 $O A$ ， $O C$ ， $B C$ 围成的区域（不含边界）为 $W$ ．
①当 $b = - 1$ 时，直接写出区域 $W$ 内的整点个数；
②若区域 $W$ 内恰有4个整点，结合函数图象，求 $b$ 的取值范围．

查看试题解析
13. 在平面直角坐标系xOy中，抛物线y=x²﹣4x+3与x轴交于点A、B（点A在点B的左侧），与y轴交于点C．

(1)、求直线BC的表达式；

(2)、垂直于y轴的直线l与抛物线交于点P（x₁ ， y₁），Q（x₂ ， y₂），与直线BC交于点N（x₃ ， y₃），若x₁＜x₂＜x₃ ，结合函数的图象，求x₁+x₂+x₃的取值范围．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = \frac{1}{2} x$ 的图象向下平移1个单位长度得到．

(1)、求这个一次函数的解析式；

(2)、当 $x > - 2$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
15. 在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．

(1)、当⊙O的半径为2时，
①在点P₁（ $\frac{1}{2}$ ，0），P₂（ $\frac{1}{2}$ ， $\frac{\sqrt{3}}{2}$ ），P₃（ $\frac{5}{2}$ ，0）中，⊙O的关联点是．
②点P在直线y=﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．

(2)、⊙C的圆心在x轴上，半径为2，直线y=﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．

查看试题解析

16. 小云在学习过程中遇到一个函数

y = \frac{1}{6} | x | (x^{2} - x + 1) (x \geq - 2)

．下面是小云对其探究的过程，请补充完整：

(1)、当

- 2 \leq x < 0

时，对于函数

y_{1} = | x |

，即

y_{1} = - x

，当

- 2 \leq x < 0

时，

y_{1}

随x的增大而，且

y_{1} > 0

；对于函数

y_{2} = x^{2} - x + 1

，当

- 2 \leq x < 0

时，

y_{2}

随x的增大而，且

y_{2} > 0

；结合上述分析，进一步探究发现，对于函数

y

，当

- 2 \leq x < 0

时，y随x的增大而．

(2)、当

x \geq 0

时，对于函数

y

，当

x \geq 0

时，y与x的几组对应值如下表：

x	0	$\frac{1}{2}$	1	$\frac{3}{2}$	2	$\frac{5}{2}$	3	$\dots$
y	0	$\frac{1}{16}$	$\frac{1}{6}$	$\frac{7}{16}$	1	$\frac{95}{48}$	$\frac{7}{2}$	$\dots$

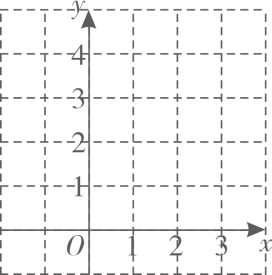
综合上表，进一步探究发现，当 $x \geq 0$ 时，y随x的增大而增大．在平面直角坐标系 $x O y$ 中，画出当 $x \geq 0$ 时的函数y的图象．

(3)、过点(0，m)（

m > 0

）作平行于x轴的直线l，结合（1）（2）的分析，解决问题：若直线l与函数

y = \frac{1}{6} | x | (x^{2} - x + 1) (x \geq - 2)

的图象有两个交点，则m的最大值是．

查看试题解析

17. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = x$ 的图象平移得到，且经过点(1，2)．

(1)、求这个一次函数的解析式；

(2)、当 $x > 1$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析
18. 对于平面直角坐标系 $x O y$ 中的图形 $M$ ， $N$ ，给出如下定义： $P$ 为图形 $M$ 上任意一点， $Q$ 为图形 $N$ 上任意一点，如果 $P$ ， $Q$ 两点间的距离有最小值，那么称这个最小值为图形 $M$ ， $N$ 间的“闭距离”，记作 $d$ （ $M$ ， $N$ ）．
已知点 $A$ （ $- 2$ ，6）， $B$ （ $- 2$ ， $- 2$ ）， $C$ （6， $- 2$ ）．

(1)、求 $d$ （点 $O$ ， $△ A B C$ ）；

(2)、记函数 $y = k x$ （ $- 1 \leq x \leq 1$ ， $k \neq 0$ ）的图象为图形 $G$ ，若 $d$ （ $G$ ， $△ A B C$ ） $= 1$ ，直接写出 $k$ 的取值范围；

(3)、 $⊙ T$ 的圆心为 $T$ （t ， 0），半径为1．若 $d$ （ $⊙ T$ ， $△ A B C$ ） $= 1$ ，直接写出t的取值范围．

查看试题解析
19. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x - \frac{1}{a}$ 与 $y$ 轴交于点A，将点A向右平移2个单位长度，得到点B，点B在抛物线上．

(1)、求点B的坐标（用含 $a$ 的式子表示）；

(2)、求抛物线的对称轴；

(3)、已知点 $P (\frac{1}{2} ， - \frac{1}{a})$ ， $Q (2 ， 2)$ ．若抛物线与线段PQ恰有一个公共点，结合函数图象，求 $a$ 的取值范围．

查看试题解析
20. 在平面直角坐标系 $x O y$ 中，直线 $y = 4 x + 4$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ ， $B$ ，抛物线 $y = a x^{2} + b x - 3 a$ 经过点 $A$ ，将点 $B$ 向右平移5个单位长度，得到点 $C$ ．

(1)、求点 $C$ 的坐标；

(2)、求抛物线的对称轴；

(3)、若抛物线与线段 $B C$ 恰有一个公共点，结合函数图象，求 $a$ 的取值范围．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，直线l： $y = k x + 1 (k \neq 0)$ 与直线 $x = k$ ，直线 $y = - k$ 分别交于点A，B，直线 $x = k$ 与直线 $y = - k$ 交于点 $C$ ．

(1)、求直线 $l$ 与 $y$ 轴的交点坐标；

(2)、横、纵坐标都是整数的点叫做整点．记线段 $A B ， B C ， C A$ 围成的区域（不含边界）为 $W$ ．
①当 $k = 2$ 时，结合函数图象，求区域 $W$ 内的整点个数；

②若区域 $W$ 内没有整点，直接写出 $k$ 的取值范围．

查看试题解析
22. 国家创新指数是反映一个国家科学技术和创新竞争力的综合指数．对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析．下面给出了部分信息：
a．国家创新指数得分的频数分布直方图（数据分成7组：

30≤x＜40，40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）；

b．国家创新指数得分在60≤x＜70这一组的是：61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5

c.40个国家的人均国内生产总值和国家创新指数得分情况统计图：

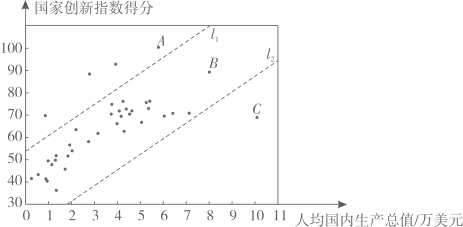
d．中国的国家创新指数得分为69.5.

（以上数据来源于《国家创新指数报告（2018）》）

根据以上信息，回答下列问题：

(1)、中国的国家创新指数得分排名世界第；

(2)、在40个国家的人均国内生产总值和国家创新指数得分情况统计图中，包括中国在内的少数几个国家所对应的点位于虚线 $l_{1}$ 的上方．请在图中用“ $○$ ”圈出代表中国的点；

(3)、在国家创新指数得分比中国高的国家中，人均国内生产总值的最小值约为万美元；（结果保留一位小数）

(4)、下列推断合理的是．
①相比于点A，B所代表的国家，中国的国家创新指数得分还有一定差距，中国提出“加快建设创新型国家”的战略任务，进一步提高国家综合创新能力；

②相比于点B，C所代表的国家，中国的人均国内生产总值还有一定差距，中国提出“决胜全面建成小康社会”的奋斗目标，进一步提高人均国内生产总值．

查看试题解析

23. 如图，P是

\overset{⌢}{A B}

与弦AB所围成的图形的外部的一定点，C是

\overset{⌢}{A B}

上一动点，连接PC交弦AB于点D．

小腾根据学习函数的经验，对线段PC，PD，AD的长度之间的关系进行了探究．

下面是小腾的探究过程，请补充完整：

(1)、对于点C在

\overset{⌢}{A B}

上的不同位置，画图、测量，得到了线段PC，PD，AD的长度的几组值，如下表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8
PC/cm	3.44	3.30	3.07	2.70	2.25	2.25	2.64	2.83
PD/cm	3.44	2.69	2.00	1.36	0.96	1.13	2.00	2.83
AD/cm	0.00	0.78	1.54	2.30	3.01	4.00	5.11	6.00

在PC，PD，AD的长度这三个量中，确定的长度是自变量，的长度和的长度都是这个自变量的函数；

(2)、在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；

(3)、结合函数图象，解决问题：当PC=2PD时，AD的长度约为cm．

查看试题解析

24. 如图，在平面直角坐标系xOy中，函数y= $\frac{k}{x}$ （x＞0）的图象与直线y=x﹣2交于点A（3，m）．

(1)、求k、m的值；

(2)、已知点P（n，n）（n＞0），过点P作平行于x轴的直线，交直线y=x﹣2于点M，过点P作平行于y轴的直线，交函数y= $\frac{k}{x}$ （x＞0）的图象于点N．
①当n=1时，判断线段PM与PN的数量关系，并说明理由；

②若PN≥PM，结合函数的图象，直接写出n的取值范围．

查看试题解析
25.
已知y是x的函数，自变量x的取值范围x＞0，下表是y与x的几组对应值：
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
下面是小腾的探究过程，请补充完整：

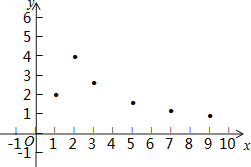(1)、如图，在平面直角坐标系xOy中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(2)、根据画出的函数图象，写出：
①x=4对应的函数值y约为
②该函数的一条性质：

查看试题解析
26. 在平面直角坐标系xOy中，抛物线y=mx²﹣2mx+m﹣1（m＞0）与x轴的交点为A，B．

(1)、求抛物线的顶点坐标；

(2)、
横、纵坐标都是整数的点叫做整点．
①当m=1时，求线段AB上整点的个数；
②若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m的取值范围．

查看试题解析
27.
如图，在平面直角坐标系xOy中，过点A（﹣6，0）的直线l₁与直线l₂：y=2x相交于点B（m，4）．

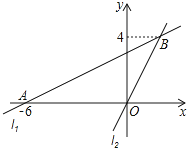(1)、求直线l₁的表达式；

(2)、过动点P（n，0）且垂于x轴的直线与l₁ ， l₂的交点分别为C，D，当点C位于点D上方时，写出n的取值范围．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中， $M (x_{1} ， y_{1}) ， N (x_{2} ， y_{2})$ 为抛物线 $y = a x^{2} + b x + c (a > 0)$ 上任意两点，其中 $x_{1} < x_{2}$ ．

(1)、若抛物线的对称轴为 $x = 1$ ，当 $x_{1} ， x_{2}$ 为何值时， $y_{1} = y_{2} = c ；$

(2)、设抛物线的对称轴为 $x = t$ ．若对于 $x_{1} + x_{2} > 3$ ，都有 $y_{1} < y_{2}$ ，求t的取值范围．

查看试题解析
29. 如图， $Q$ 是 $\overset{⌢}{A B}$ 与弦 $A B$ 所围成的图形的内部的一定点， $P$ 是弦 $A B$ 上一动点，连接 $P Q$ 并延长交 $\overset{⌢}{A B}$ 于点 $C$ ，连接 $A C$ ．已知 $A B = 6 cm$ ，设 $A$ ， $P$ 两点间的距离为 $x$ $cm$ ， $P$ ， $C$ 两点间的距离为 $y_{1} cm$ ， $A$ ， $C$ 两点间的距离为 $y_{2} cm$ ．
小腾根据学习函数的经验，分别对函数 $y_{1}$ ， $y_{2}$ 随自变量 $x$ 的变化而变化的规律进行了探究．
下面是小腾的探究过程，请补充完整：

(1)、按照下表中自变量 $x$ 的值进行取点、画图、测量，分别得到了 $y_{1}$ ， $y_{2}$ 与 $x$ 的几组对应值；
$x / cm$
0
1
2
3
4
5
6
$y_{1} / cm$
$5.62$
$4.67$
$3.76$
$2.65$
$3.18$
$4.37$
$y_{2} / cm$
$5.62$
$5.59$
$5.53$
$5.42$
$5.19$
$4.73$
$4.11$

(2)、在同一平面直角坐标系 $x O y$ 中，描出补全后的表中各组数值所对应的点（ $x$ ， $y_{1}$ ），（ $x$ ， $y_{2}$ ），并画出函数 $y_{1}$ ， $y_{2}$ 的图象；

(3)、结合函数图象，解决问题：当 $△ A P C$ 为等腰三角形时， $A P$ 的长度约为 $cm$ ．

查看试题解析

$x / cm$	0	1	2	3	4	5	6
$y_{1} / cm$	$5.62$	$4.67$	$3.76$		$2.65$	$3.18$	$4.37$
$y_{2} / cm$	$5.62$	$5.59$	$5.53$	$5.42$	$5.19$	$4.73$	$4.11$

x	…	1	2	3	5	7	9	…
y	…	1.98	3.95	2.63	1.58	1.13	0.88	…