浙江省台州市椒江区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-20 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、﹣1 B、 C、 D、2. 如图所示的四个图形中,∠1和∠2是内错角的是( )
 A、① B、② C、③ D、④3. 下列调查中,不适合用普查的是( )A、旅客上飞机前的安检 B、某大学师生新冠疫苗接种情况 C、了解一批口罩的质量 D、全国第七次人口普查4. 已知x<y,则下列结论不成立的是( )A、x﹣2<y﹣2 B、3x+1<3y+1 C、﹣2x<﹣2y D、5. 在平面直角坐标系中,点P( , )一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )A、
A、① B、② C、③ D、④3. 下列调查中,不适合用普查的是( )A、旅客上飞机前的安检 B、某大学师生新冠疫苗接种情况 C、了解一批口罩的质量 D、全国第七次人口普查4. 已知x<y,则下列结论不成立的是( )A、x﹣2<y﹣2 B、3x+1<3y+1 C、﹣2x<﹣2y D、5. 在平面直角坐标系中,点P( , )一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )A、 B、
B、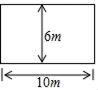 C、
C、 D、
D、 7. 一个正整数的平方根为±m,则比这个正整数大5的数的算术平方根是( )A、m+5 B、 C、m2+5 D、8. 若关于x的一元一次不等式组 的解集为x>1,则a的取值范围是( )A、a>1 B、a≤1 C、a<1 D、a≥19. 如图,BD为∠ABC的角平分线,AD∥BC,∠BDC=90°,∠A与∠C的数量关系为( )
7. 一个正整数的平方根为±m,则比这个正整数大5的数的算术平方根是( )A、m+5 B、 C、m2+5 D、8. 若关于x的一元一次不等式组 的解集为x>1,则a的取值范围是( )A、a>1 B、a≤1 C、a<1 D、a≥19. 如图,BD为∠ABC的角平分线,AD∥BC,∠BDC=90°,∠A与∠C的数量关系为( ) A、∠A+∠C=180° B、∠A=2∠C C、∠A﹣ ∠C=90° D、 ∠A+∠C=90°10. 当实数m,n满足m-2n=1,则称点P(m+2, )为创新点,若关于x,y的方程组 的解为坐标的点Q(x,y)为创新点,则a的值为( )A、 B、 C、 D、
A、∠A+∠C=180° B、∠A=2∠C C、∠A﹣ ∠C=90° D、 ∠A+∠C=90°10. 当实数m,n满足m-2n=1,则称点P(m+2, )为创新点,若关于x,y的方程组 的解为坐标的点Q(x,y)为创新点,则a的值为( )A、 B、 C、 D、二、填空题
-
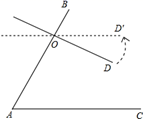
11. 命题“同位角相等”是(填“真”或“假”,)命题12. 为了分析全市2021年全区7800名初中毕业生的数学考试成绩,共抽取30本试卷,每本试卷都是20份,则样本容量为.13. 如图,∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD为75°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转度.
 14. 已知x、y满足方程组 ,则x﹣y的值为15. 在平面直角坐标系中,点A(5,3),B(a,3),若0<AB≤6,则a的取值范围为16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的点,且点B的横坐标为2n(n为正整数)记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为12时,m的值为 , 点B的横坐标为2022时,m的值为
14. 已知x、y满足方程组 ,则x﹣y的值为15. 在平面直角坐标系中,点A(5,3),B(a,3),若0<AB≤6,则a的取值范围为16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的点,且点B的横坐标为2n(n为正整数)记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为12时,m的值为 , 点B的横坐标为2022时,m的值为
三、解答题
-
17. 计算:18. 解不等式组 并把它的解集在数轴(如图)上表示出来.
 19. 三角形ABC经过平移后得到三角形A1B1C1 , 已知点A(﹣3,3),其对应点为A1(3,1),三角形ABC经过平移后得到三角形A1B1C1 , 点P的对应点为P1(a+6,b﹣2).
19. 三角形ABC经过平移后得到三角形A1B1C1 , 已知点A(﹣3,3),其对应点为A1(3,1),三角形ABC经过平移后得到三角形A1B1C1 , 点P的对应点为P1(a+6,b﹣2). (1)、直接写出点B1、C1的坐标;(2)、P(a,b)是三角形ABC的边AC上任意一点,请写出平移三角形A1B1C1内对应点P1的坐标;(3)、将三角形ABC向下平移2个单位,再向右平移1个单位,得到三角形A2B2C2 , 在图中画出A2B2C2.20. 如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
(1)、直接写出点B1、C1的坐标;(2)、P(a,b)是三角形ABC的边AC上任意一点,请写出平移三角形A1B1C1内对应点P1的坐标;(3)、将三角形ABC向下平移2个单位,再向右平移1个单位,得到三角形A2B2C2 , 在图中画出A2B2C2.20. 如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.∵∠BHC=∠FHD,∠GFH+∠BHC=180°,
∴∠GFH+∠FHD=180°
∴FG平行BD
∴_▲_
∵BD平分∠ABC,
∴_▲_
∴∠1=∠2
 21. 为了迎接英语期末测试,某校七年级开展了一次“英语单词”竞赛,现随机抽取了部分学生的比赛结果为样本进行整理,并绘制了直方图,请根据图中提供的信息,完成下列问题
21. 为了迎接英语期末测试,某校七年级开展了一次“英语单词”竞赛,现随机抽取了部分学生的比赛结果为样本进行整理,并绘制了直方图,请根据图中提供的信息,完成下列问题成绩x(分)
频数(人)
频率
50≤x<60
6
12%
60≤x<70
10
20%
70≤x<80
m
32%
80≤x<90
14
n%
90≤x<100
4
8

根据所给信息,解答下列问题:
(1)、共抽取了名学生调查,m= , n= ,(2)、补全频数分布直方图;(3)、如果成绩不低于80分为良好,请你估计该校参加本次比赛的700名学生中获得“良好”的学生有多少人?22. 一个数的算术平方根为2m﹣6,它的平方根为±(m-1),求m的值.23. 劳技老师准备购买若干个花篮和笔筒,带着同学学习编织手艺,已知同时购买一个花篮和一个笔筒按标价打八折省1.9元,一个花篮标价是一个笔筒标价的2倍少4元.(1)、购买一个花篮和一个笔筒的标价各是多少元?(2)、根据学校实际情况,现在需要购买花篮和笔筒共800个,要求总费用不超过3681元,并且花篮的数量大于笔筒数量的1/4,请问学校哪些方案?24. 在如图所示的平面直角坐标系中,A(1,3),B(3,1),将线段AB平移至CD,C(m,-1),D(1,n) (1)、m= , n=(2)、点P的坐标是(c,0)
(1)、m= , n=(2)、点P的坐标是(c,0)①设∠ABP= ,请写出∠BPD和∠PDC之间的数量关系(用含 的式子表示,若有多种数量关系,选择一种加以说明)
②当三角形PAB的面积不小于3且不大于10,求点p的横坐标C的取值范围(直接写出答案即可)