吉林省中考数学真题汇编(近三年)4 图形的性质----三角形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
 A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线2. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、
A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线2. 在 中, , .用无刻度的直尺和圆规在BC边上找一点D , 使 为等腰三角形.下列作法错误的是( )A、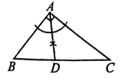 B、
B、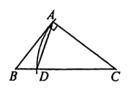 C、
C、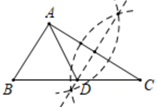 D、
D、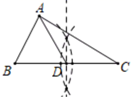 3. 将一副三角尺按如图所示的方式摆放,则 的大小为( )
3. 将一副三角尺按如图所示的方式摆放,则 的大小为( ) A、 B、 C、 D、4. 如图,在 中, , .按下列步骤作图:①分别以点B和点C为圆心,大于 一半的长为半径作圆弧,两弧相交于点M和点N;②作直线 ,与边 相交于点D,连结 .下列说法不一定正确的是( )
A、 B、 C、 D、4. 如图,在 中, , .按下列步骤作图:①分别以点B和点C为圆心,大于 一半的长为半径作圆弧,两弧相交于点M和点N;②作直线 ,与边 相交于点D,连结 .下列说法不一定正确的是( )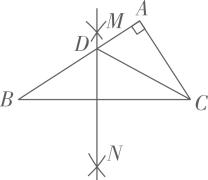 A、 B、 C、 D、5. 如图,在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D。使∠ADC=2∠B,则符合要求的作图痕迹是( )A、
A、 B、 C、 D、5. 如图,在△ABC中,∠ACB为钝角。用直尺和圆规在边AB上确定一点D。使∠ADC=2∠B,则符合要求的作图痕迹是( )A、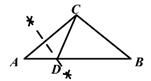 B、
B、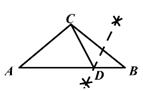 C、
C、 D、
D、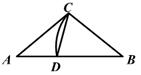
二、填空题
-
6. 如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
 7. 如图,已知线段 ,其垂直平分线 的作法如下:①分别以点 和点 为圆心, 长为半径画弧,两弧相交于 , 两点;②作直线 .上述作法中 满足的条作为 1.(填“ ”,“ ”或“ ”)
7. 如图,已知线段 ,其垂直平分线 的作法如下:①分别以点 和点 为圆心, 长为半径画弧,两弧相交于 , 两点;②作直线 .上述作法中 满足的条作为 1.(填“ ”,“ ”或“ ”) 8. 将一副三角板按如图所示的方式摆放,点D在边AC上, ,则 的大小为度.
8. 将一副三角板按如图所示的方式摆放,点D在边AC上, ,则 的大小为度.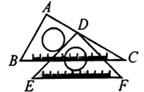 9. 如图,在 中,D,E分别是边 , 的中点.若 的面积为 .则四边形 的面积为 .
9. 如图,在 中,D,E分别是边 , 的中点.若 的面积为 .则四边形 的面积为 .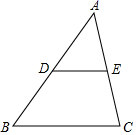 10. 正五边形的一个外角的大小为度.11. 如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°。过线段AB上的点C作CD⊥AB交PQ于点D,则∠CDB的大小为 度。
10. 正五边形的一个外角的大小为度.11. 如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°。过线段AB上的点C作CD⊥AB交PQ于点D,则∠CDB的大小为 度。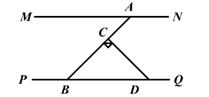 12. 如图, 为 边 延长线上一点,过点 作 .若 , ,则 °.
12. 如图, 为 边 延长线上一点,过点 作 .若 , ,则 °.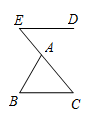 13. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .
13. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .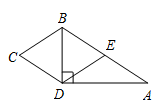 14. 如图,在平面直角坐标系中,抛物线 ( 是常数,且 )与 轴交于 、 两点(点 在点 的左边),与 轴交于点 .连结 ,将线段 绕点 顺时针旋转 ,得到线段 ,连结 .当 最短时, 的值为 .
14. 如图,在平面直角坐标系中,抛物线 ( 是常数,且 )与 轴交于 、 两点(点 在点 的左边),与 轴交于点 .连结 ,将线段 绕点 顺时针旋转 ,得到线段 ,连结 .当 最短时, 的值为 .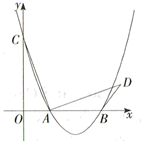
三、解答题
-
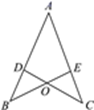
15. 如图,点D在AB上,点E在AC上,BE和CD相交于点O , AB=AC , ∠B=∠C.求证:AD=AE
 16. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .
16. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .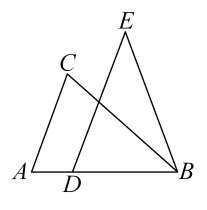
求证: .
17. 墙壁及淋浴花洒截面如图所示,已知花洒底座 与地面的距离 为 ,花洒 的长为 ,与墙壁的夹角 为43°.求花洒顶端 到地面的距离 (结果精确到 )(参考数据: , , )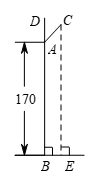
四、作图题
-
18. 图①、图②、图③均是 的正方形网格,每个小正方形的边长均为1.每个小正方形的顶点称为格点,点A、B、C均为格点,只用无刻度的直尺,分别在给定的网格中找一格点M , 按下列要求作图:
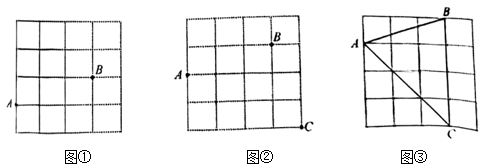 (1)、在图①中,连结MA、MB , 使 .(2)、在图②中,连结MA、MB、MC , 使 .(3)、在图③中,连结MA、MC , 使 .19. 图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .
(1)、在图①中,连结MA、MB , 使 .(2)、在图②中,连结MA、MB、MC , 使 .(3)、在图③中,连结MA、MC , 使 .19. 图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .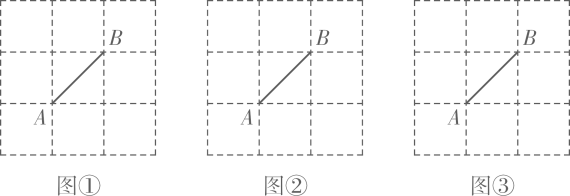
要求:
a.在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;
b.三个图中所画的三角形的面积均不相等;
c.点C在格点上.
五、综合题
-
20. 如图①,在 中, , , 是斜边 上的中线,点 为射线 上一点,将 沿 折叠,点 的对应点为点 .
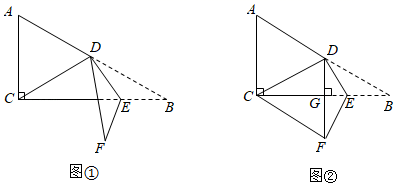 (1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.21. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上。在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法。
(1)、若 .直接写出 的长(用含 的代数式表示);(2)、若 ,垂足为 ,点 与点 在直线 的异侧,连接 ,如图②,判断四边形 的形状,并说明理由;(3)、若 ,直接写出 的度数.21. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上。在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法。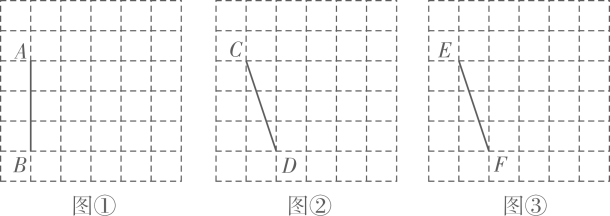 (1)、在图①中以线段AB为边画一个△ABM,使其面积为6。(2)、在图②中以线段CD为边画一个△CDN,使其面积为6。(3)、在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°22. 如图,在 中, , , ,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD . 作点A关于直线PD的对称点 ,连结 、 .设点P的运动时间为t秒.
(1)、在图①中以线段AB为边画一个△ABM,使其面积为6。(2)、在图②中以线段CD为边画一个△CDN,使其面积为6。(3)、在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°22. 如图,在 中, , , ,点D为边AC的中点.动点P从点A出发,沿折线AB—BC以每秒1个单位长度的速度向点C运动,当点P不与点A、C重合时,连结PD . 作点A关于直线PD的对称点 ,连结 、 .设点P的运动时间为t秒.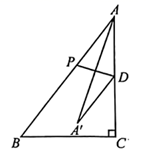 (1)、线段AD的长为 .(2)、用含t的代数式表示线段BP的长.(3)、当点 在 内部时,求t的取值范围.(4)、当 与 相等时,直接写出t的值.23. 如图, 是等边三角形, ,动点P从点A出发,以 的速度沿 向点B匀速运动,过点P作 ,交折线 于点Q,以 为边作等边三角形 ,使点A,D在 异侧.设点P的运动时间为 , 与 重叠部分图形的面积为 .
(1)、线段AD的长为 .(2)、用含t的代数式表示线段BP的长.(3)、当点 在 内部时,求t的取值范围.(4)、当 与 相等时,直接写出t的值.23. 如图, 是等边三角形, ,动点P从点A出发,以 的速度沿 向点B匀速运动,过点P作 ,交折线 于点Q,以 为边作等边三角形 ,使点A,D在 异侧.设点P的运动时间为 , 与 重叠部分图形的面积为 .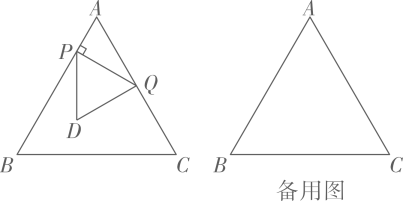 (1)、 的长为 (用含 的代数式表示).(2)、当点D落在边 上时,求x的值.(3)、求y关于x的函数解析式,并写出自变量x的取值范围.24. 如图①,在 中, , , .点P从点A出发,沿折线AB- BC以每秒5个单位长度的速度向点C运动,同时点D从点C出发,沿CA以每秒2个单位长度的速度向点A运动,点P到达点C时,点P、D同时停止运动.当点P不与点A、C重合时,作点P关于直线AC的对称点Q,连结PQ交AC于点E,连结DP、DQ.设点P的运动时间为t秒.。
(1)、 的长为 (用含 的代数式表示).(2)、当点D落在边 上时,求x的值.(3)、求y关于x的函数解析式,并写出自变量x的取值范围.24. 如图①,在 中, , , .点P从点A出发,沿折线AB- BC以每秒5个单位长度的速度向点C运动,同时点D从点C出发,沿CA以每秒2个单位长度的速度向点A运动,点P到达点C时,点P、D同时停止运动.当点P不与点A、C重合时,作点P关于直线AC的对称点Q,连结PQ交AC于点E,连结DP、DQ.设点P的运动时间为t秒.。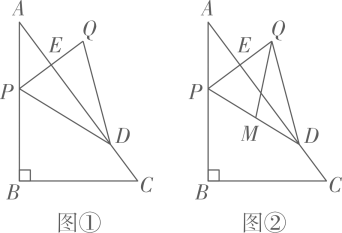 (1)、当点P与点B重合时,求t的值.(2)、用含 的代数式表示线段 的长.(3)、当 为锐角三角形时,求t的取值范围.(4)、如图②,取 的中点M,连结 .当直线 与 的一条直角边平行时,直接写出t的值.25. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .
(1)、当点P与点B重合时,求t的值.(2)、用含 的代数式表示线段 的长.(3)、当 为锐角三角形时,求t的取值范围.(4)、如图②,取 的中点M,连结 .当直线 与 的一条直角边平行时,直接写出t的值.25. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .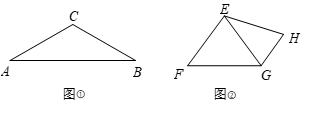 (2)、理解运用
(2)、理解运用若顶角为120°的等腰三角形的周长为 ,则它的面积为;
(3)、如图②,在四边形 中, .①求证: ;
②在边 上分别取中点 ,连接 .若 , ,直接写出线段 的长.
(4)、类比拓展顶角为 的等腰三角形的底边与一腰的长度之比为(用含 的式子表示).