浙江省杭州市上城区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式是二元一次方程的是（）

A、2x²＋y＝0 B、 $x = \frac{1}{y} + 2$ C、x﹣y D、 $\frac{x + 2 y}{4} - 3 y = 0$

查看试题解析
2. “潮涌”是2022年杭州亚运会会徽，钱塘江和钱江潮头是会徽的形象核心，如图是会徽的一部分，在以下四个选项中，能由该图经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 要使分式 $\frac{1}{2 x - 4}$ 有意义，x的取值范围是（）

A、x≠﹣2 B、x≠2 C、x＝2 D、x≠﹣1

查看试题解析
4. 如图，直线EF与直线AB，CD相交.图中所示的各个角中，能看做∠1的内错角的是（）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
5. 计算4²×2021＋48×2021＋6²×2021的结果为（）

A、2021 B、20210 C、202100 D、2021000

查看试题解析
6. 如图为某服装品牌公司2016～2020年销售额年增长率的统计图，则这5年中，该公司销售额最大的是（）年.

A、2020 B、2019 C、2018 D、2017

查看试题解析
7. 一个长方形的面积是15x³y⁵﹣10x⁴y⁴＋20x³y² ，一边长是5x³y² ，则它的另一边长是（）

A、2y³﹣3xy²＋4 B、3y³﹣2xy²＋4 C、3y³＋2xy²＋4 D、2xy²﹣3y³＋4

查看试题解析
8. 如图，∠B＋∠DCB＝180°，AC平分∠DAB，且∠D∶∠DAC＝5∶2，则∠D的度数是（）

A、100° B、105° C、110° D、120°

查看试题解析
9. 甲瓶糖水含糖量为 $\frac{1}{m}$ ，乙瓶糖水含糖量为 $\frac{1}{n}$ ，从甲、乙两瓶中各取质量相等的糖水混合制成新糖水的含糖量为（）

A、 $\frac{1}{m n}$ B、 $\frac{m + n}{m n}$ C、 $\frac{m + n}{2 m n}$ D、由所取糖水质量而定

查看试题解析
10. 已知方程组 ${\begin{matrix} a + b = 4 \\ a b = 2 \end{matrix}$ ，下列说法正确的是（）
①a²＋b²＝12；②（a﹣b）²＝8；③ $\frac{1}{a} + \frac{1}{b} = 2$ ；④ $\frac{b^{}}{a} + \frac{a}{b} = 6$ .

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知一组数据的频数为24，频率为0.8，则样本容量为.

查看试题解析
12. 已知 ${\begin{matrix} x = - 5 \\ y = 2 \end{matrix}$ 是方程x＋3y＝1的一个解，请再写出这个方程的一个解.

查看试题解析
13. 若mn＝3，m﹣n＝7，则m²n﹣mn²＝.

查看试题解析
14. 2020年某企业生产医用口罩，为扩大产量，添置了甲、乙两条生产线.甲生产线每天生产口罩的数量是乙生产线每天生产口罩数量的2倍，两生产线各加工6000箱口罩，甲生产线比乙生产线少用5天.则甲、乙两生产线每天共生产的口罩箱数为.

查看试题解析
15. 如果两个多项式有公因式，则称这两个多项式为关联多项式，若x²﹣25与（x＋b）²为关联多项式，则b＝；若（x＋1）（x＋2）与A为关联多项式，且A为一次多项式，当A＋x²﹣6x＋2不含常数项时，则A为.

查看试题解析
16. 计算（﹣s＋t）（﹣s﹣t）＝.

查看试题解析

三、解答题

17. 分解因式

(1)、a²﹣6ab＋9b²；

(2)、a²b﹣16b.

查看试题解析
18. 静静同学解分式方程 $\frac{- 6 x}{(x - 1) (x - 3)} - \frac{2}{x - 1} = \frac{5}{3 - x}$ 的过程如下：
去分母得：﹣6x﹣2（3﹣x）＝5（x﹣1）

去括号得：﹣6x﹣6﹣2x＝5x﹣5

移项得：﹣6x﹣2x﹣5x＝﹣5﹣6

合并同类项得：﹣13x＝﹣11

两边同除以13得：x $= \frac{13}{11}$ 经检验x $= \frac{13}{11}$ 是方程的解.

静静的解答过程是否有错误？如果有错误，请写出正确的解答过程.

查看试题解析
19. 为了普及新冠病毒的有关知识，某校举办了一场关于新冠病毒的知识竞赛.为了解此次知识竞赛成绩的情况，随机抽取了部分参赛学生的成绩，得到如下频数分布直方图（每组含前一个边界值，不含后一个边界值）.请根据该直方图，回答下列问题.

(1)、数据分组时的组距为分.

(2)、自左至右分别为第1，2，3，4组，频数最大的是哪一组？并说出该组的组中值.

(3)、学校决定为成绩在80分以上（包括80分）的学生颁发优秀证书，若该校共有800名学生，请估计能拿到优秀证书的学生人数.

查看试题解析
20. 如图，政府规划由西向东修一条公路.从A修至B后为了绕开村庄，改为沿南偏东25°方向修建BC段，在C处又改变方向修建CD段，测得∠BCD＝70°，在D处继续改变方向，朝与出发时相同的方向修至E.

(1)、补全施工路线示意图，求∠CDE的度数；

(2)、原计划在AB的延长线上依次修建两个公交站M，N（均在CD右侧），连结DM和MN，求∠CDM与∠DMN的数量关系.

查看试题解析
21. 亮亮计算一道整式乘法的题（3x﹣m）（2x﹣5），由于亮亮在解题过程中，抄错了第一个多项式中m前面的符号，把“﹣”写成了“＋”，得到的结果为6x²﹣5x﹣25.

(1)、求m的值；

(2)、计算这道整式乘法的正确结果.

查看试题解析
22. 如图，在长方形ABCD中，放入8个完全相同的小长方形.

(1)、每个小长方形的长和宽分别是多少厘米？

(2)、图中阴影部分面积为多少平方厘米？

查看试题解析
23. 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.

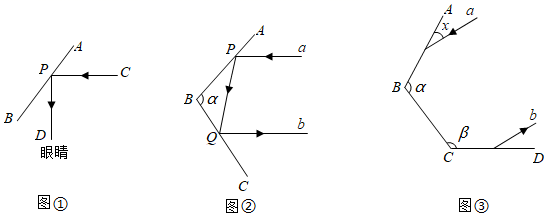(1)、提词器的原理如图①，AB表示平面镜，CP表示入射光线，PD表示反射光线，∠CPD＝90°，求∠APC的度数；

(2)、自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线，a∥b.平面镜AB与BC的夹角∠ABC＝ $α$ ，求 $α$ .

(3)、如图③，若 $α$ ＝108°，设平面镜CD与BC的夹角∠BCD＝ $β$ （90°＜ $β$ ＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出 $β$ 的度数.（可用含x的代数式表示）.

查看试题解析