浙江省杭州市滨江区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列是二元一次方程的是（）

A、 $x - 2 = \frac{1}{2} x$ B、 $4 x + 3 y = 1$ C、 $x + \frac{2}{y} = 0$ D、 $2 x - y = x^{2}$

查看试题解析
2. 要使分式 $\frac{x - 1}{x - 2}$ 有意义，则 $x$ 的取值应满足（）

A、 $x \neq 2$ B、 $x \neq 1$ C、 $x = 2$ D、 $x = 1$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $2 a^{3} - a^{3} = 1$ C、 $x \cdot x^{2} = x^{3}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
4. 为了解某中学2500名学生家长对“骑电动车需戴头盔”的态度，从中随机调查400名家长，结果有380名家长持赞成态度，则下列说法正确的是（）

A、调查方式是全面调查 B、该校只有380名家长持赞成态度 C、样本是400 D、该校约有95%的家长持赞成态度

查看试题解析
5. 如图，下列说法不正确的是（）

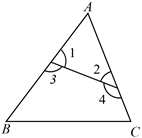A、 $∠ 1$ 和 $∠ A$ 是同旁内角 B、 $∠ 2$ 和 $∠ B$ 是内错角 C、 $∠ 3$ 和 $∠ A$ 是同位角 D、 $∠ 4$ 和 $∠ C$ 是同旁内角

查看试题解析
6. 下列计算正确的是（）

A、 $(x + 2 y) (x - 2 y) = x^{2} - 2 y^{2}$ B、 $(x - y) (- x - y) = - x^{2} - y^{2}$ C、 ${(x - y)}^{2} = x^{2} - 2 x y + y^{2}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
7. 下列因式分解正确的是（）

A、 $x^{2} - 9 = (x - 9) (x + 9)$ B、 $a^{3} - a^{2} + a = a (a^{2} - a)$ C、 ${(x - 1)}^{2} - 2 (x - 1) + 1 = {(x - 1)}^{2}$ D、 $2 x^{2} - 8 x y + 8 y^{2} = 2 {(x - 2 y)}^{2}$

查看试题解析
8. 某班级第一次用160元买奖品，第二次又用600元买奖品，已知第二次买的奖品数量是第一次买的奖品数量的3倍，但单价比第一次的单价多2元，设第一次买奖品的单价是 $x$ 元，则下列所列方程正确的是（）

A、 $\frac{600}{x} = 3 \times \frac{160}{x + 2}$ B、 $\frac{600}{x + 2} = 3 \times \frac{160}{x}$ C、 $3 \times \frac{600}{x} = \frac{160}{x + 2}$ D、 $3 \times \frac{600}{x + 2} = \frac{160}{x}$

查看试题解析
9. 一个长方体模型的长、宽、高分别是4a（cm），3a（cm），a（cm），某种油漆每千克可漆面积为 $\frac{1}{2} a$ （cm），则漆这个模型表面需要的油漆是（）千克.

A、 $76 a$ B、 $38 a$ C、 $76 a^{2}$ D、38 $a^{2}$

查看试题解析
10. 已知无论x取何值，等式 $(x + a) (x + b) = x^{2} + 2 x + n$ 恒成立，则关于代数式 $a^{3} b + a b^{3} - 2$ 的值有下列结论：①交换a，b的位置，代数式的值不变；②该代数式的值是非正数；③该代数式的值不会小于－2，上述结论正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 钓鱼岛列岛上最小的岛是飞濑岛，它的面积，它的面积为0.0008平方公里，用科学记数法表示飞濑岛的面积约为平方公里.

查看试题解析

12. 为了解某校初一年级女生的身高情况，随机抽取60名学生的身高如表：

分组	145.5~150.5	150.5~155.5	155.5~160.5	160.5~165.5
频数	6	13		m
频率			0.55

则m的值为.

查看试题解析

13. 一块长为25cm，宽为15cm的长方形木板中间有一条裂缝（如图甲）.若把裂缝右边的一块向右平移2cm（如图乙），则产生的裂缝的面积是 ${cm}^{2}$ .

查看试题解析
14. 若 $a - b = 7$ ， $a b = 10$ ，则 ${(a + b)}^{2} =$ .

查看试题解析
15. 已知关于x，y的方程组为 ${\begin{matrix} x + y = 3 + 2 a \\ x - y = 1 + a \end{matrix}$ ，则 $2^{x} \div {(2^{y})}^{3}$ 的值为.

查看试题解析
16. 如图，将一条两边互相平行的纸带折叠，折痕为DE， $∠ A B E$ 平分线所在直线与 $∠ E D H$ 平分线所在直线相交于点F，若 $∠ F = \frac{3}{4} ∠ B E D$ ，则 $∠ 1$ 的度数为.

查看试题解析

三、解答题

17. 计算：

(1)、（－3）²＋（π＋3）⁰

(2)、（－2a）³b³÷（6a³b²）

查看试题解析
18. 解下列方程（组）：

(1)、 ${\begin{matrix} 2 x + y = 7 ， \\ x - 2 y = 1 ； \end{matrix}$

(2)、 $\frac{1}{x - 2} - \frac{4}{x^{2} - 4} = 0$

查看试题解析
19. 某校七年级英语演讲比赛结束后，老师对比赛成绩（得分均为整数）进行整理，并分别绘制成扇形统计图和频数直方图，部分信息如下：

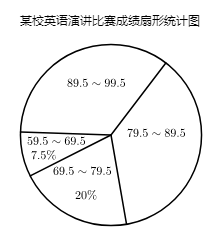
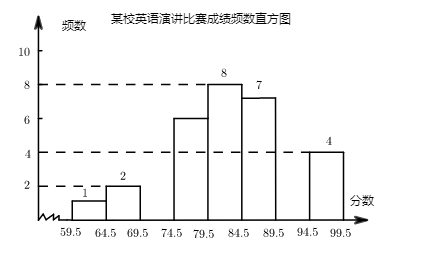(1)、问该校共有多少名学生参加此次英语演讲比赛？

(2)、分数在“89.5~94.5”的学生有多少名？

查看试题解析
20. 先化简，再求值：

(1)、（a－2）（a＋3）＋3（a－1），其中a＝1.

(2)、 $\frac{a + 2}{a^{2} - 1} \cdot \frac{a - 1}{a^{2} + 4 a + 4} \div \frac{1}{a + 2}$ ，其中a＝2.

查看试题解析
21. 如图，点D，F，H，E都在△ABC的边上，且DE $/ /$ AC，∠1＋∠2＝180°.

(1)、求证：AE $/ /$ HF；

(2)、若∠1＝∠3，试猜想∠BHF与∠CFH的数量关系，并说明理由.

查看试题解析
22. 甲地到乙地全程5.5km，小明从甲地走路去乙地，其中有一段上坡路、一段平路和一段下坡路.如果上坡路的平均速度为2km/h，下坡路的平均速度为5km/h.

(1)、若小明走路从甲地到乙地需 $\frac{7}{4}$ 小时，从乙地走路到甲地需 $\frac{19}{10}$ 小时，来回走平路分别都用了 $\frac{1}{4}$ 小时，求出小明从甲地到乙地的上坡路和下坡路的路程（请用方程组的方法解）.

(2)、若小明从甲地到乙地，平路上的平均速度为v（km/h），上坡和下坡走的路程分别为1.5km和2km.若小明从乙地到甲地所用的时间与从甲地到乙地的时间相同，求小明从乙地到甲地平路上走的平均速度（用含v的代数式表示）.

查看试题解析
23. 如图，4张长为x，宽为y（x＞y）的长方形纸片拼成一个边长为（x＋y）的正方形ABCD.

(1)、用含x，y的代数式表示图中所有阴影部分面积的和；

(2)、当正方形ABCD的周长是正方形EFGH周长的三倍时，求 $\frac{x}{y}$ 的值；

(3)、在（2）的条件下，用题目条件中的4张长方形纸片，m张正方形ABCD纸片和n张正方形EFHG纸片（m，n为正整数），拼成一个大的正方形（拼接时无空隙、无重叠），当m，n为何值时，拼成的大正方形的边长最小？

查看试题解析