四川省乐山市市中区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x+1＝5的解是（）

A、x＝﹣6 B、x＝6 C、x＝4 D、x＝﹣4

查看试题解析
2. 内角和与外角和相等的图形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
3. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
4. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
5. 一个等腰三角形的两边长分别是3和7，则它的周长为（）

A、17 B、15 C、13 D、13或17

查看试题解析
6. 能铺满地面的正多边形的组合是（）

A、正五边形和正方形 B、正六边形和正方形 C、正八边形和正方形 D、正十边形和正方形

查看试题解析
7. 某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10元，则该商品每件的进价为（）

A、120元 B、110元 C、100元 D、90元

查看试题解析
8. 如图，在△ABC中，∠B＝90°，AB＝10.将△ABC沿着BC的方向平移至△DEF，若平移的距离是5，则图中阴影部分的面积为（）

A、25 B、50 C、35 D、70

查看试题解析
9. 如图，将四边形纸片ABCD沿EF折叠，点A落在A₁处，若∠1+∠2＝90°，则∠A的度数是（）

A、45° B、40° C、35° D、30°

查看试题解析
10. 无论m取何有理数， ${\begin{array}{l} x = m + 2 \\ y = 3 m + 4 \end{array}$ 都是方程y＝kx+b（k≠0）的解，则k﹣b＝（）

A、﹣5 B、﹣1 C、1 D、5

查看试题解析

二、填空题

11. 若2x^3k^﹣5＝3是关于x的一元一次方程，则k＝.

查看试题解析
12. 如图，自行车的车身为三角形结构，这样做根据的数学道理是.

查看试题解析
13. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？设有x匹大马，y匹小马，根据题意可列方程组为．

查看试题解析
14. 如图所示，在△ABC中，∠B＝30°，∠C＝80°，AD是△ABC的角平分线，AE是△ABC的高，则∠DAE＝.

查看试题解析
15. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 7 - 2 x \leq - 1 \end{array}$ 只有3个正整数解，则m的取值范围为.

查看试题解析
16. 如图，在直角三角形ABC中，AC＝3，BC＝4，AB＝5，且AC在直线l上，将△ABC绕点A顺时针旋转到位置①得到点P₁ ，将位置①的三角形绕点P₁顺时针旋转到位置②得到点P₂ ， …，按此规律继续旋转，直到得到点P₂₀₂₁为止（P₁ ， P₂ ， P₃…在直线l上）.则（1）AP₃＝；AP₂₀₂₁＝.

查看试题解析

三、解答题

17. 解下列方程（组）

(1)、 $\frac{2 x + 5}{3} - \frac{3 x - 2}{4} =$ 1.

(2)、 ${\begin{array}{l} 2 x - 3 y = 7 \\ x + 3 y = - 1 \end{array}$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} 4 x > 2 x - 6 \\ \frac{x - 1}{3} \leq \frac{x + 5}{9} \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
19. 如图所示的正方形网格中，每个小正方形的边长均为1个单位， $Δ A B C$ 的三个顶点都在格点上.

（1）在网格中画出 $Δ A B C$ 向下平移3个单位得到的 $Δ A_{1} B_{1} C_{1}$ ；
（2）在网格中画出 $Δ A B C$ 关于直线 $m$ 对称的 $Δ A_{2} B_{2} C_{2}$ ；
（3）在直线 $m$ 上画一点 $P$ ，使得 $| P A - P C_{2} |$ 的值最大.

查看试题解析
20. 已知关于x，y的方程 ${\begin{array}{l} x - 2 y = 3 \\ 2 x + y = 6 a \end{array}$ .

(1)、当a＝1时，求代数式3x﹣y的值；

(2)、若该方程组的解满足不等式x﹣y＜2，求a的最大整数值.

查看试题解析
21. 如图，△ABD≌△EBC，AB=3cm，BC=6cm，

(1)、求DE的长.

(2)、若A、B、C在一条直线上，则DB与AC垂直吗？为什么？

查看试题解析
22. 如图，△ABC中，AD是中线，将△ABD旋转后与△ECD重合.

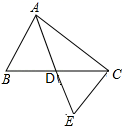(1)、旋转中心是点，旋转了度；

(2)、如果AB＝3，AC＝4，求中线AD长的取值范围.

查看试题解析
23. 为了抓住峨眉山文化艺术节的商机，某商店决定购进A、B两种艺术纪念品.若购进A种纪念品6件，B种纪念品3件，需要750元；购进A种纪念品4件，B种纪念品5件，需要650元.

(1)、求购进A、B两种纪念品每件各需要多少元？

(2)、若该商店决定购进这两种纪念品共120件，考虑到市场需求和资金周转，用于购买这120件纪念品的资金不超过9500元，那么该商店最多购进A种纪念品多少件？

查看试题解析
24. 如图，在△ABC中，AD平分∠BAC，点E为AC中点，AD与BE相交于点F.

(1)、若∠ABC＝40°，∠C＝80°，求∠ADB的度数；

(2)、过点B作BH⊥AD交AD延长线于点H，作△ABH关于AH对称的△AGH，设△BFH，△AEF的面积分别为S₁ ， S₂ ，若S_△BCG＝4，试求S₁﹣S₂的值.

查看试题解析
25. 阅读理解：
例1.解方程|x|＝2，因为在数轴上到原点的距离为2的点对应的数为±2，所以方程|x|＝2的解为x＝±2.

例2.解不等式|x﹣1|＞2，在数轴上找出|x﹣1|＝2的解（如图），因为在数轴上到1对应的点的距离等于2的点对应的数为﹣1或3，所以方程|x﹣1|＝2的解为x＝﹣1或x＝3，因此不等式|x﹣1|＞2的解集为x＜﹣1或x＞3.

参考阅读材料，解答下列问题：

(1)、方程|x﹣2|＝3的解为；

(2)、解不等式：|x﹣2|≤1.

(3)、解不等式：|x﹣4|+|x+2|＞8.

(4)、对于任意数x，若不等式|x+2|+|x﹣4|＞a恒成立，求a的取值范围.

查看试题解析
26. 在△ABC中，∠BCA＞∠BAC，三个内角的平分线交于点O.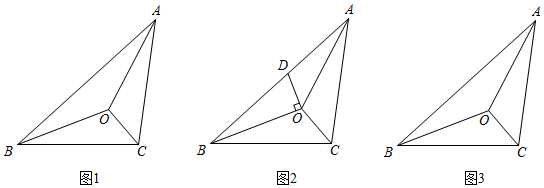

(1)、填空：如图1，若∠BAC＝36°，则∠BOC的大小为；

(2)、点D在BA，AC边上运动.
①如图2，当点D在BA边上运动时，连接OD，若OD⊥OB.试说明：∠ADO＝∠AOC；

②如图3，BO的延长线交AC于点E，当点D在AC边上运动（不与点E重合）时，过点D作DP⊥BO，垂足为点P，请在图3中画出符合条件的图形，并探索∠ADP、∠ACB、∠BAC者之间的数量关系.

查看试题解析