陕西省汉中市汉台区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期：2021-08-20 类型：期末考试
一、单选题
-
1. 下面4个汉字中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列运算正确的是（ ）A、a+a3＝a4 B、（a+b）2＝a2+b2 C、a10÷a2＝a5 D、（a2）3＝a63. 目前，世界上能制造出的最小晶体管的长度只有0.00000004m，将0.00000004用科学记数法表示为（ ）A、0.4×108 B、4×108 C、4×10﹣8 D、﹣4×1084. 一副直角三角板如图放置，点C在FD的延长线上，AB//CF，∠F=∠ACB=90°，则∠DBC的度数为（ ）
A、10° B、15° C、18° D、30°5. 若x2﹣mx+4是完全平方式，则m的值为（ ）A、2 B、4 C、±2 D、±46. 下列各式能直接用平方差公式计算的是（ ）A、 B、 C、 D、7. 如图，△ABC中，AD为△ABC的角平分线，BE为△ABC的高，∠C=70°，∠ABC=48°，那么∠3是（ ）
A、59° B、60° C、56° D、22°8. 一水池放水，先用一台抽水机工作一段时间后停止，然后再调来一台同型号抽水机，两台抽水机同时工作直到抽干．设从开始工作的时间为 ，剩下的水量为 ．下面能反映 与 之间的关系的大致图象是（ ）A、
B、
C、
D、
9. 已知 则 的大小关系是（ ）A、 B、 C、 D、10. 如图，在△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线交AC，AD，AB于点E，O，F，则图中全等三角形的对数是（ ）
A、3对 B、4对 C、5对 D、6对二、填空题
-
11. 计算：若x+3y﹣2＝0，则2x•8y＝.12. 一个角的补角为 ，那么这个角的余角的度数为 .13. 如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点，若∠MON=35°，则∠GOH=.
14. 如图，BD是△ABC的中线，点E、F分别为BD、CE的中点，若△AEF的面积为3cm2 ， 则△ABC的面积是 cm2 ．
三、解答题
-
15. 计算下列各题：(1)、 ；(2)、（﹣3xy2）2•（﹣6x3y）÷（9x4y5）.16. 先化简，再求值：
（a＋2）2－（a＋1）（a－1），其中a＝ ．
17. 如图△ABC，求作直线MN，使△ABC沿该直线折叠后点A落在边BC上的点P处.（尺规作图，不写作法，保留作图痕迹）
18. 已知a+b＝6，ab＝2，求下列各式的值(1)、a2+b2；(2)、（a﹣b）2.19. 如图，AB//CD，点E在AB上，EF平分∠BED，∠FEG＝102°，∠D＝62°，求∠AEG的度数.
20. 若（x2+ax+8）（x2﹣3x+b）的乘积中不含x2和x3项，求a，b的值.21. 如图，AB//CD，AC＝BD点F是BD上一点，且BF＝5，连接AF并延长交CD的延长线于点E，若AF＝EF，求AC的长.
22. 请将下列事件发生的概率标在图中.
(1)、抛出的篮球会下落；(2)、从装有3个红球、7个白球的口袋中取一个球，恰好是红球（这些球除颜色外完全相同）；(3)、掷一枚质地均匀的硬币，硬币落下后正面朝上.23. 如图：小刚站在河边的A点处，在河的对面（小刚的正北方向）的B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了30步到达一棵树C处，接着再向前走了30步到达D处，然后他左转 直行，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他共走了140步.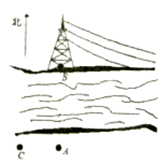
(1)、根据题意，画出示意图；(2)、如果小刚一步大约50厘米，估计小刚在点A处时他与电线塔的距离，并说明理由.24. 小昊家与文具超市相距1080米，小昊从家出发，沿笔直的公路匀速步行12分钟来到文具超市买笔记本，买完以后，便沿着原路匀速跑步6分钟返回家中，小吴离家距离y（米）与离家时间x（分钟）的关系如图所示：
(1)、根据图象回答，小昊在文具超市停留了几分钟？(2)、求小昊从文具超市返回家中的速度比从家去文具超市的速度快多少？(3)、请直接写出小昊从家出发后多少分钟离家距离为810米？25. 已知：△ABC中，∠ACB＝90°，AC＝BC，过点A作AD⊥AE，且AE＝AD.
(1)、如图1，当点D在线段BC上时，过点E作EH⊥AC于H，连接DE.求证：EH＝AC：(2)、如图2，当点D在CB延长线上时，连接BE交AC的延长线于点M.求证：BM＝EM：