江苏省盐城市2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-20 类型:期末考试
一、单选题
-
1. 若 ,则下列式子成立的是( )A、 B、 C、 D、2. 下列长度的三根小木棒,能搭成三角形的是( )A、1、2、3 B、2、3、4 C、3、3、6 D、2、3、73. 下列运算结果等于 的是( )A、 B、 C、 D、4. 下列式子中,能用平方差公式运算的是( )A、 B、 C、 D、5. 如图,在长方形纸片 中, ,将长方形纸片沿 折叠,点 落在点 处, 交边 于点 ,若 ,则 等于( )
 A、 B、 C、 D、6. 如图,4张边长分别为 、 的长方形纸片围成一个正方形,从中可以得到的等式是( )
A、 B、 C、 D、6. 如图,4张边长分别为 、 的长方形纸片围成一个正方形,从中可以得到的等式是( )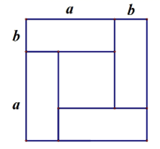 A、 B、 C、 D、7. 计算 的值为( )A、 B、 C、2 D、8. 下列命题中,真命题的个数为( )
A、 B、 C、 D、7. 计算 的值为( )A、 B、 C、2 D、8. 下列命题中,真命题的个数为( )( 1 )如果 ,那么 ;
( 2 )内错角相等,两直线平行;
( 3 )垂线段最短;
( 4 )若 ,则 .
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. “某种小客车载有乘客 人,它的最大载客量为14人”,用不等式表示其数量之间的关系为.10. 我国是世界上水能源最丰富的国家之一,水能源经济可开发装机容量为402000000千瓦,数据402000000用科学记数法表示为.11. 在 中, , ,则 为.12. 若一个多边形的每个外角均为 ,则这个多边形的边数为.13. 命题“对顶角相等”的逆命题是14. 二元一次方程2x+y=5的正整数解为 .15. 已知 , ,则 .16. 若不等式组 有解,则 的取值范围是.
三、解答题
-
17. 计算: .18. 分解因式:(1)、 ;(2)、 .19. 解方程组或不等式组:(1)、 ;(2)、 .20. 已知方程 的解为负数,求正整数 的值.21. 填写下列推理中的空格:
已知:如图,点 、 、 、 在同一条直线上, , .
求证:
证明:∵ (已知)
∴ __▲_( )
又∵ (已知)
∴ _▲_( )
∴_▲_ _▲_( )
∴ ( )
 22. 如图, 的网格中,每个小方格的边长为一个单位,将 向右平移2格,再向下平移1格,得 .
22. 如图, 的网格中,每个小方格的边长为一个单位,将 向右平移2格,再向下平移1格,得 . (1)、画出 ;(2)、线段 与 的大小关系为;(3)、 与 的位置关系为;(4)、求 的面积.23. 已知:如图,在 中, , , 为边 上一点,连接 交 于点 , .
(1)、画出 ;(2)、线段 与 的大小关系为;(3)、 与 的位置关系为;(4)、求 的面积.23. 已知:如图,在 中, , , 为边 上一点,连接 交 于点 , .求证: 平分 .
 24. (阅读感悟)
24. (阅读感悟)对于方程组的问题,有时候要求的结果不是每个未知数的值,而是求关于未知数的代数式的值.如已知实数 、 满足 ,求 和 的值.
方法一:解方程组,分别求出 、 的值,代入代数式求值;
方法二:仔细观察两个方程中未知数的系数之间的关系,通过适当变形整体求代数式的值.解法如下:
①-②,得: ;①+②×2,得: .
比较:方法一运算量较大,是常规思路;方法二运算较为简单,这种解题思路就是通常所说的“整体思想”.
(问题解决)
(1)、已知二元一次方程组 ,则 ; .(2)、某班级因组织活动购买奖品.买13支铅笔、4块橡皮、2本笔记本共需48元;买25支铅笔、7块橡皮、3本笔记本共需84元.则购买5只铅笔、5块橡皮、5本笔记本共需元.(3)、对于实数 、 ,定义新运算: ,其中 、 、 是常数,等式右边是通常的加减法和乘法运算.已知 , ,那么 的值是.25. (问题探索)已知线段 与一点 .试探索 与 、 数量之间的关系.
探索该问题时,需要对线段 与点 的位置关系进行分类讨论:
 (1)、如图1,点 在线段 上时,有 ;(2)、如图2、3,点 在线段 (或线段 )的延长线上时,有 ;(3)、如图4,点 在线段 所在直线外时,有 , 理由是.(4)、画 ,在 的两边上分别取点 、 ,在 的内部取一点 ,连接 、 探索 与 、 、 之间的数量关系,并证明你的结论.
(1)、如图1,点 在线段 上时,有 ;(2)、如图2、3,点 在线段 (或线段 )的延长线上时,有 ;(3)、如图4,点 在线段 所在直线外时,有 , 理由是.(4)、画 ,在 的两边上分别取点 、 ,在 的内部取一点 ,连接 、 探索 与 、 、 之间的数量关系,并证明你的结论.