广西壮族自治区钦州市浦北县2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数中，是无理数的是（）

A、－3 B、0 C、 $\frac{1}{3}$ D、 $\sqrt{6}$

查看试题解析
2. 下列调查中，适合采用抽样调查的是（）

A、了解七（3）班同学的身高情况 B、学校招聘教师，对应聘人员面试 C、检查乘坐动车的旅客是否携带了违禁物品 D、了解全县学生在疫情期间的线上学习情况

查看试题解析
3. 下列计算错误的是（）

A、 $\sqrt{0.16} ＝ \pm 0.4$ B、 $\sqrt{{(- 3)}^{2}} = 3$ C、 ${(\sqrt{5})}^{2} = 5$ D、 $\sqrt[3]{8} = 2$

查看试题解析
4. 我们经常将调查、收集得来的数据用各类统计图进行整理与表示．下列统计图中，能凸显由数据所表现出来的部分与整体的关系的是（）

A、条形图 B、扇形图 C、折线图 D、频数分布直方图

查看试题解析
5. 下列命题中，是假命题的是（）

A、垂线段最短 B、对顶角相等 C、同旁内角互补 D、等角的余角相等

查看试题解析
6. 下列实数中，不是x+4≥2的解的是（）

A、﹣3 B、﹣2 C、0 D、3.5

查看试题解析
7. 如图，将△ABC平移得到△A'B'C'，下列结论中不一定成立的是（）

A、AA'//BB' B、BB'//CC' C、AA'＝BB' D、BC＝A'C'

查看试题解析
8. 二元一次方程3x+y＝8的非负整数解共有（）

A、2对 B、3对 C、4对 D、5对

查看试题解析
9. 如图，李老师家在学校的南偏东55°方向，距离是500米，则学校在李老师家的（）

A、北偏西35°方向，相距500米处 B、北偏东35°方向，相距500米处 C、北偏西55°方向，相距500米处 D、北偏东55°方向，相距500米处

查看试题解析
10. 如图，已知直线 $l_{1} // l_{2}$ ，将一个含45°角的三角尺按图中方式放置，如果 $∠ 1 = 24 °$ ，那么 $∠ 2$ 的度数为（）

A、24° B、45° C、66° D、21°

查看试题解析
11. 不等式组 ${\begin{matrix} x + 5 < 5 x + 1 \\ x - m > 1 \end{matrix}$ 的解集是x＞1，则m的取值范围是（）

A、m≥1 B、m≤1 C、m≥0 D、m≤0

查看试题解析
12. 如图，在平面直角坐标系中，点A从原点O出发，按A→A₁→A₂→A₃→A₄→A₅…依次不断移动，每次移动1个单位长度，则A₂₀₂₁的坐标为（）

A、（673，﹣1） B、（673，1） C、（674，﹣1） D、（674，1）

查看试题解析

二、填空题

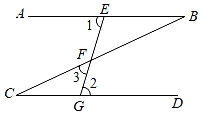
13. 为了解七年级共650名学生的体质情况，从中抽取了50名学生进行体能测试并统计分析，在此次调查中，样本容量是 .

查看试题解析
14. 在平面直角坐标系中，已知点P在第四象限，距高x轴2个单位长度，距离y轴3个单位长度，则点P的坐标为.

查看试题解析
15. 如图，已知∠1＝∠2＝75°，∠3＝50°，则∠B的大小为 .

查看试题解析
16. 如图，将长方形分成四个区域，其中A、B两正方形区域的面积分别是1和7，则剩余区域的面积是 .

查看试题解析
17. 已知a+b﹣5的平方根是±3，a﹣b+4的立方根是2.则3a﹣b+4的值为 .

查看试题解析

三、解答题

18. 计算：

(1)、 $\sqrt{5} (\sqrt{5} + 5) - 2 \sqrt{5}$ ；

(2)、 $\sqrt[3]{27} - | \sqrt{2} - 3 |$ .

查看试题解析
19. 解不等式组： ${\begin{matrix} 6 x > 3 (x - 1) \\ \frac{x + 3}{2} \leq \frac{2 x + 6}{3} \end{matrix}$ ，并利用数轴确定不等式组的解集.

查看试题解析
20. 如图，点A（﹣2，1）在平面直角坐标系内，请解答下列问题：

(1)、建立适当的平面直角坐标系，描出点B（3，1），C（2，3）的位置，并顺次连接成三角形ABC；

(2)、在（1）条件下，三角形ABC的面积为；

(3)、在（1）条件下，把三角形ABC向左平移2个单位长度，再向下平移4个单位长度得到三角形A₁B₁C₁ ，画出三角形A₁B₁C₁ ，并写出点A₁的坐标.

查看试题解析

21. 为庆祝中国共产党建党100周年，育才中学共1000名学生参加了学校举行的党史知识竞赛（满分100分）.从中抽取部分学生的成绩进行统计分析.

收集数据：77 71 80 63 52 88 73 53 68 100 64 85 95 59 70 50 85 99 86 65 89 66 65 52 82 65 75 62 75 68 75 75 80 65 65 76 86 79 67 78 86 77 79 62 70 59 66 76 98 79

整理、分析数据：

分组	划记	频数
50≤x＜60	正一	6
60≤x＜70		a
70≤x＜80	正正正一	16
80≤x＜90	正正	10
90≤x≤100		b
合计	50	50

根据以上信息，解答下列问题：

(1)、求出表格中的a＝_▲，b＝_▲_ ；并把频数分布直方图补充完整；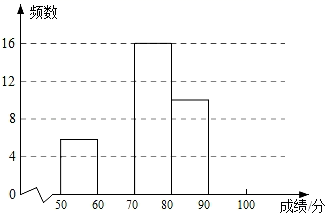

(2)、从直方图中你能得到什么信息（写出两条即可）？

(3)、如果成绩达到90分（含90分）以上者为优秀，可推荐参加进入决赛，那么请你估计该校进入决赛的学生大约有多少人.

查看试题解析

22. 如图，已知∠1＋∠2＝180^o ， ∠3＝∠B，试说明∠DEC＋∠C＝180^o.请完成下列填空：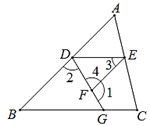

解：∵∠1＋∠2＝180^o（已知）

又∵∠1＋∠4＝180^o（平角定义）

∴∠2＝∠4（      ）

∴_▲_∥_▲_（      ）

∴∠3 ＝ ∠ADE（      ）

又∵∠3＝∠B（已知）

∴∠ADE＝∠B（等量代换）

∴BC∥_▲_（      ）

∴∠DEC＋∠C＝180^o（      ）

查看试题解析
23. 为改善学校环境卫生面貌，计划购买A、B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元；购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.

(1)、求每个A型垃圾箱和B型垃圾箱各多少元？

(2)、学校计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个（两种都需要购买），则最多可以购买B型垃圾箱多少个？有几种购买方案？

查看试题解析
24. 问题情境：如图1，AB∥CD ， ∠PAB＝130°，∠PCD＝120°，求∠APC的度数．小明的思路是：过点P作PE∥AB ，通过平行线性质来求∠APC ．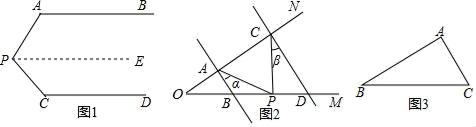

(1)、按小明的思路，请你求出∠APC的度数；

(2)、问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P在B，D两点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；

(3)、联想拓展：在(2)的条件下，如果点P在B ， D两点外侧运动时(点P与点O ， B ， D三点不重合)，请直接写出∠APC与α，β之间的数量关系；

(4)、解决问题：我们发现借助构造平行线的方法可以帮我们解决许多问题，随着以后的学习你还会发现平行线的许多用途．试构造平行线解决以下问题．
已知：如图3，三角形ABC ，求证：∠A+∠B+∠C＝180°

查看试题解析