福建省漳州市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图标为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 计算 ${(2 x^{3})}^{2}$ 的结果是（）.

A、 $2 x^{5}$ B、 $2 x^{6}$ C、 $4 x^{5}$ D、 $4 x^{6}$

查看试题解析
3. 如图，下列说法错误的是（）

A、∠1与∠3是对顶角 B、∠3与∠4是内错角 C、∠2与∠6是同位角 D、∠3与∠5是同旁内角

查看试题解析
4. 如果等腰三角形的两边长分别为3和6，那么它的周长为（）

A、9 B、12 C、15 D、12或15

查看试题解析
5. 如图， $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $B C$ 边上的中线，若 $∠ B = 70 °$ ，则 $∠ B A D$ 等于（）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
6. 声音在空气中传播的速度 $v$ （简称声速）与空气温度 $t$ 的关系（如下表所示），则下列说法错误的是（）

温度 $t / ° C$

-20

-10

0

10

20

30

声速 $v / (m/s)$

318

324

330

336

342

348

A、温度越高，声速越快 B、在这个变化过程中，自变量是声速 $v$ ，因变量是温度 $t$ C、当空气温度为 $20 ° C$ ，声速为 $342 m/s$ D、声速 $v$ 与温度 $t$ 之间的关系式为 $v = \frac{3}{5} t + 330$

查看试题解析
7. 木箱里装有仅颜色不同的8张红色和若干张蓝色卡片，随机从木箱里摸出1张卡片记下颜色后再放回，经过多次的重复试验，发现摸到蓝色卡片的频率稳定在0.6附近，则估计木箱中蓝色卡片有（）

A、18张 B、16张 C、14张 D、12张

查看试题解析
8. 将一副三角尺按下列几种方式摆放，则能使 $∠ α = ∠ β$ 的摆放方式为（）

A、 B、 C、 D、

查看试题解析
9. 如图，在 $△ A B C$ 中， $A D$ 是 $∠ B A C$ 的平分线， $D E ⊥ A C$ ，垂足为 $E$ ，若 $A B = 12$ ， $D E = 4$ ，则 $△ A B D$ 的面积是（）

A、4 B、12 C、24 D、48

查看试题解析
10. 有足够多张如图所示的 $A$ 类、 $B$ 类正方形卡片和 $C$ 类长方形卡片，如果要拼一个长为 $(3 a + 2 b)$ 、宽为 $(2 a + b)$ 的大长方形，则需要 $C$ 类卡片的张数为（）

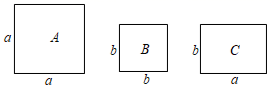A、3 B、4 C、6 D、7

查看试题解析

二、填空题

11. 数据0.000000006用科学记数法可表示为.

查看试题解析
12. 计算： $2021^{0} + {(\frac{1}{5})}^{- 1} =$ .

查看试题解析
13. 如图，已知 $A B$ 是线段 $C D$ 的垂直平分线，点 $P$ 在 $A B$ 上，若 $P C = 5$ ，则 $P D$ 长为.

查看试题解析
14. 如图是 $4 \times 4$ 正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中任选出一个也涂成黑色，则使整个涂黑部分为轴对称图形的概率是.

查看试题解析
15. 若 $m = 3^{a}$ ， $3 m = 3^{b}$ ，则 $b =$ .（用含 $a$ 的式子表示）

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 6$ ， $B C = 8$ ， $A C = 10$ . $A D$ 平分 $∠ B A C$ 且交 $B C$ 于点 $D$ ，点 $E$ 和 $F$ 分别是线段 $A B$ 和 $A D$ 上的动点，则 $F E + F B$ 的最小值为.

查看试题解析

三、解答题

17. 计算： $(a + 2 b) (a - 2 b) + (a^{3} b + 4 a b^{3}) \div a b$ .

查看试题解析
18. 先化简，再求值： ${(2 x - y)}^{2} - x (x - 4 y)$ ，其中 $x = 3$ ， $y = - 2$ .

查看试题解析
19. 如图，把两根钢条 $A B$ ， $C D$ 的中点连在一起，其交点为 $O$ ，可以做成一个测量工件内槽宽的工具（卡钳），只要量得 $A C$ 的长度，就可知工件的内径 $B D$ 的长度，请说明理由.

查看试题解析
20. 请在下列括号内填上相应步骤的理由.
已知：如图， $A B / / C D$ ， $D A ⊥ A C$ ，垂足为 $A$ ， $∠ 1 = ∠ 2$ ，试说明： $F E ⊥ A C$ .

解：因为 $A B / / C D$ （已知），

所以 $∠ 1 = ∠ D$ （             ）.

因为 $∠ 1 = ∠ 2$ （已知），

所以 $∠ 2 = ∠ D$ （等量代换），

所以 $E F / / A D$ （             ），

所以 $∠ C E F = ∠ C A D$ （             ）.

因为 $A D ⊥ A C$ （已知），

所以 $∠ C A D = 90 °$ （垂直的定义），

所以 $∠ C E F = 90 °$ （             ），

所以 $F E ⊥ A C$ （垂直的定义）.

查看试题解析
21. 一个袋中装有4个红球，6个白球，8个黑球，每个球除颜色外其余完全相同.

(1)、求从袋中随机摸出一个球是白球的概率；

(2)、从袋中摸出6个白球和 $a (a > 2)$ 个红球，再从剩下的球中摸出一个球.
①若事件“再摸出的球是红球”为不可能事件，求 $a$ 的值；

②若事件“再摸出的球是黑球”为随机事件，求这个事件的概率.

查看试题解析
22. 如图，直线 $a / / b$ ，点 $A$ ，点 $C$ 在直线 $b$ 上，点 $B$ 在直线 $a$ 上，连接 $A B$ .

(1)、在直线 $a$ 上求作点 $D$ ，使得 $C D / / A B$ ；（要求：尺规作图，保留作图痕迹，不写作法）

(2)、在（1）的条件下，若 $A B = 7$ ，求 $C D$ 的长.

查看试题解析
23. 如图1，点 $P$ 沿边框以 $B \to C \to D \to E \to F \to A$ 为路径，从 $B$ 到 $A$ 以 $2 cm/s$ 的速度运动， $△ A B P$ 的面积为 $S ({cm}^{2})$ 与运动时间 $t (s)$ 的关系如图2所示， $A B = 8 cm$ .

(1)、当 $0 \leq t \leq 4$ 时，求 $S$ 与运动时间 $t$ 的关系式；

(2)、求图2中 $m$ ， $n$ 的值；

(3)、求点 $P$ 在运动过程中 $S$ 的最大值.

查看试题解析
24. 已知 $x = a - 2015$ ， $y = 2021 - a$ ， $x y = 5$ .

(1)、求 $x^{2} + y^{2}$ 的值；

(2)、求 ${(x - y)}^{2}$ 的值；

(3)、求 $a$ 的值.

查看试题解析
25. 如图，在 $△ A B C$ 和 $△ B C D$ 中， $A C = C D$ ， $∠ B A C + ∠ B D C = 180 °$ ，在 $B D$ 的延长线上取点 $E$ ，使 $D E = A B$ ，连接 $C E$ .

(1)、试说明： $∠ A B C = ∠ D B C$ ；

(2)、连接 $A D$ 交 $B C$ 于点 $F$ ，若 $∠ A B D = 60 °$ ， $∠ A D B = 40 °$ ，试说明： $B D = A B + A F$ .

查看试题解析

温度 $t / ° C$	-20	-10	0	10	20	30
声速 $v / (m/s)$	318	324	330	336	342	348