福建省三明市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 计算 20210 的结果是（   ）
    A、2021 B、1 C、0 D、12021

    查看试题解析

  • 2. 新型冠状病毒微粒直径约为0.1微米，0.1微米等于0.0000001米，将0.0000001用科学记数法表示为（  ）
    A、1×10﹣7 B、1×10﹣6 C、0.1×10﹣7 D、0.1×10﹣6

    查看试题解析

  • 3. 下列事件中，是必然事件的是（  ）
    A、任意买一张电影票，座位号是2的倍数 B、走到一个红绿灯路口时，前方正好是红灯 C、三明市区明天会下雨 D、从一个只有3个红球和1个白球的盒子里摸出两个球，一定会摸到红球

    查看试题解析

  • 4. 下列图形属于轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 已知∠A＝38°，则∠A的补角的度数是（  ）
    A、52° B、62° C、142° D、162°

    查看试题解析

  • 6. 如图，下列条件不能判定AB∥CD的是（  ）

    A、∠1＝∠3 B、∠1＝∠2 C、∠2＝∠3 D、∠2+∠4＝180°

    查看试题解析

  • 7. 一个等腰三角形的两条边长分别为2、5，则它的周长是（   ）
    A、12 B、9 C、9或12 D、以上答案都不对

    查看试题解析

  • 8. 已知声音在空气中的传播速度与空气的温度有关，在一定范围内，其关系如表所示：

    温度℃

    ﹣20

    ﹣10

    0

    10

    20

    30

    传播速度/（m/s）

    319

    325

    331

    337

    343

    349

    下列说法错误的是（  ）

    A、自变量是温度，因变量是传播速度 B、温度越高，传播速度越快 C、当温度为10℃时，声音5s可以传播1655m D、温度每升高10℃，传播速度增加6m/s

    查看试题解析

  • 9. 如图，BD是△ABC的中线，点E，F分别为BD，CE的中点，若△ABC的面积为12.则△AEF的面积是（  ）

    A、2 B、3 C、4 D、6

    查看试题解析

  • 10. 小红和小玉是同班同学，也是邻居，某天早晨，小红7：10先出发去学校，走了一段后，在途中停下吃早餐，后来发现上学时间快到了，就跑步到学校；小玉骑自行车沿相同路线到学校，如图是她们从家到学校已走的路程S（米）和所用的时间t（分钟）的关系图，则下列说法中错误的是（  ）

    A、小红家到学校的路程是1200米 B、小玉骑自行车的速度是240米/分 C、小玉骑自行车7：20追上小红 D、小红从家到达学校的平均速度为80米/分

    查看试题解析

二、填空题

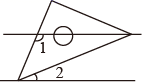
  • 11. 计算：x2•x3＝.

    查看试题解析

  • 12. 如图所示，小明将一个含有45°角的直角三角板放在两条平行线上，若∠1＝115°，则∠2的度数为 .

    查看试题解析

  • 13. 如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DC=3，则点D到AB的距离是

    查看试题解析

  • 14. 将某中学九年级的全体教师按年龄分成老、中青三组，情况如表所示，则表中a的值是 .

    老年组

    中年组

    青年组

    人数

    9

    15

    a

    频率

    b

    0.5

    c

    查看试题解析

  • 15. 如图，在△ACD中，∠CAD＝90°，AC＝4，AD＝6，AB∥CD，E是CD上一点，BE交AD于点F，若AB＝DE，则图中阴影部分的面积为 .

    查看试题解析

  • 16. 如图，点P为∠AOB内一点，分别作点P关于OA，OB的对称点P1 ， P2 ， 连接P1P2交OA于点M，交OB于点N，若∠P1PP2＝132°，则∠MPN＝.

    查看试题解析

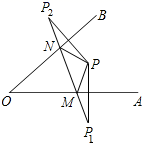
三、解答题

  • 17. 计算：
    (1)、3m2•（2m2n）2÷6m5；
    (2)、a（3a﹣1）+（1﹣a）（3a+2）.

    查看试题解析

  • 18. 先化简，再求值： [(x−2y)2−(x−y)(x+y)−2y2]÷y ，其中 x=−1 ， y=−2 .

    查看试题解析

  • 19. 如图，在4×4的正方形方格中，有5个小正方形被涂上了阴影，请分别在下列两个图中再选择两个空白的小正方形并涂上阴影，使得图中整个阴影部分成为轴对称图形.

    查看试题解析

  • 20. 某车间的甲、乙两名工人同时生产某种零件，他们生产的零件数y（个）与生产时间t（小时）的关系如图所示.

    (1)、根据图象填空：在生产过程中，因机器故障停止生产小时.
    (2)、根据图象回答谁在哪一段时间内的生产速度最快？并求该段时间内，他每小时生产零件的个数.

    查看试题解析

  • 21. 在一个不透明的口袋中放入3个红球和7个白球，它们除颜色外完全相同.
    (1)、求从口袋中随机摸出一个球是红球的概率；
    (2)、现从口袋中取出若干个白球，并放入相同数量的红球，充分摇匀后，要使从口袋中随机摸出一个球是红球的概率是 45 ，问取出了多少个白球？

    查看试题解析

  • 22. 如图，△ABC中，点D在BC边上.

    (1)、在AC边求作点E，使得DE∥AB；（要求：尺规作图，不写作法，保留作图痕迹）
    (2)、在（1）的条件下，若∠ABC＝40°，∠ACB＝2∠CDE，求∠ACB的度数.

    查看试题解析

  • 23. 如图，AD，CE是△ABC的两条高，它们交于点F，且AE＝CE.

    (1)、试说明：△AEF≌△CEB；
    (2)、若AB＝AC，试说明：AF＝2CD.

    查看试题解析

  • 24. 利用完全平方公式（a±b）2＝a2±2ab+b2 ， 可以解决很多的数学问题.

    例如：若a+b＝3，ab＝1，求a2+b2的值.

    解：因为a+b＝3，ab＝1，

    所以（a+b）2＝9，

    所以a2+b2+2ab＝9.

    所以a2+b2+2×1＝9.

    得a2+b2＝7.

    根据上面的解题思路与方法，解决下列问题：

    (1)、若x﹣y＝4，x2+y2＝40，求xy的值；
    (2)、若（2022﹣x）（x﹣2020）＝﹣2021，求（2022﹣x）2+（x﹣2020）2的值；
    (3)、如图，点C是线段AB上的一点，分别以AC，BC为直角边向外作等腰直角三角形，其中∠ACD＝∠BCE＝90°，若AB＝6，S△ACD+S△BCE＝12，求△ACE的面积.

    查看试题解析

  • 25. 如图①，在△ABC中，AD⊥BC，垂足为D，AD＝BD＝CD.

    (1)、求∠C的度数；
    (2)、如图②，点E，F分别是AB，AC上的点，且AE＝CF，连接DE，DF，判断DE和DF的关系，并说明理由；
    (3)、在（2）的条件下，过D作DG⊥AB，垂足为G，试说明：AF＝CF+2EG.

    查看试题解析