福建省泉州市2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-20 类型:期末考试
一、单选题
-
1. 下列方程中,解为x=1的是( )A、x+1=1 B、x﹣1=1 C、2x﹣2=0 D、2. 不等式 在数轴上表示正确的是( )A、
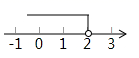 B、
B、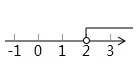 C、
C、 D、
D、 3. 小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,瓷砖形状可以是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形4. 下列图形分别是等边三角形、正方形、正五边形、等腰直角三角形,其中既是轴对称又是中心对称图形的是( )A、
3. 小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,瓷砖形状可以是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形4. 下列图形分别是等边三角形、正方形、正五边形、等腰直角三角形,其中既是轴对称又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 一个三角形的两边长分别是4和9,则它的第三边长可能是( )A、4 B、5 C、8 D、136. 下列不等式组中,无解的是( )A、 B、 C、 D、7. 若 是关于x,y的二元一次方程3k=5+3x+2y的一个解,则k的值( )A、2 B、3 C、4 D、68. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设总共有x两银子,根据题意所列方程正确的是( )A、7x﹣4=9x﹣8 B、 C、7x+4=9x+8 D、9. 如右图,五边形ABCDE的一个内角∠A =110°,则∠1+ ∠2+ ∠3+ ∠4等于( )
5. 一个三角形的两边长分别是4和9,则它的第三边长可能是( )A、4 B、5 C、8 D、136. 下列不等式组中,无解的是( )A、 B、 C、 D、7. 若 是关于x,y的二元一次方程3k=5+3x+2y的一个解,则k的值( )A、2 B、3 C、4 D、68. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设总共有x两银子,根据题意所列方程正确的是( )A、7x﹣4=9x﹣8 B、 C、7x+4=9x+8 D、9. 如右图,五边形ABCDE的一个内角∠A =110°,则∠1+ ∠2+ ∠3+ ∠4等于( ) A、360° B、290° C、270° D、250°10. 若关于x,y的二元一次方程组 的解为 则方程组 的解为( )A、 B、 C、 D、
A、360° B、290° C、270° D、250°10. 若关于x,y的二元一次方程组 的解为 则方程组 的解为( )A、 B、 C、 D、二、填空题
-
11. 已知a>b,则﹣2a﹣2b(填“>”、“<”或“=”号).12. 由3x+y=5,得到用x表示y的式子为y=.13. 为建设书香校园,某中学的图书馆藏书量增加20%后达到2.4万册,则该校图书馆原来图书有 万册.14. 如图, ,∠C=90°,点D在线段AC上,点E在线段CB延长线上,则∠1+∠E=°.
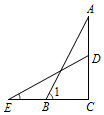 15. 如图, 沿着射线BC的方向平移到 DEF的位置,若点E是BC的中点,BF=18cm,则平移的距离为 cm.
15. 如图, 沿着射线BC的方向平移到 DEF的位置,若点E是BC的中点,BF=18cm,则平移的距离为 cm. 16. 如图,在 中,点D在BC边上,∠BAC=80°,∠ABC=50°,射线DC绕点D逆时针旋转一定角度α,交AC于点E,∠ABC的平分线与∠ADE的平分线交于点P.下列结论:
16. 如图,在 中,点D在BC边上,∠BAC=80°,∠ABC=50°,射线DC绕点D逆时针旋转一定角度α,交AC于点E,∠ABC的平分线与∠ADE的平分线交于点P.下列结论:①∠C=50°;
②∠P= ∠BAD;
③α=2∠P﹣∠BAD;
④若∠ADE=∠AED,则∠BAD=2α.
其中正确的是 .(写出所有正确结论的序号)

三、解答题
-
17. 解方程组: .18. 解不等式组: .19. 若代数式4x﹣5与3x﹣6的值互为相反数,求x的值.20. 作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
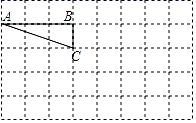 (1)、将△ABC向右平移5个单位得到△A′B′C′;(2)、将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;(3)、连结EC′,则△A′EC′是 三角形.21. 如图,在 ABC中,∠A=62°,∠ABC=48°.
(1)、将△ABC向右平移5个单位得到△A′B′C′;(2)、将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;(3)、连结EC′,则△A′EC′是 三角形.21. 如图,在 ABC中,∠A=62°,∠ABC=48°. (1)、求∠C的度数;(2)、若BD是AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.22. 如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F.
(1)、求∠C的度数;(2)、若BD是AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.22. 如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F. (1)、若∠EAD=60°,求∠DFE的度数;(2)、若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.23. 红星商场购进A,B两种型号空调,A型空调每台进价为m元,B型空调每台进价为n元,5月份购进5台A型空调和7台B型空调共43000元;6月份购进7台A型空调和6台B型空调共45000元.(1)、求m,n的值;(2)、7月份该商场计划购进这两种型号空调共78000元,其中B型空调的数量不少于12台,试问有哪几种进货方案?24. 已知x,y同时满足x+3y=4﹣a,x﹣5y=3a.(1)、当a=4时,求x﹣y的值;(2)、试说明对于任意给定的数a,x+y的值始终不变;(3)、若y>1﹣m,3x﹣5≥m,且x只能取两个整数,求m的取值范围.25. 阅读理解:如图1,在 ABC中,D是BC边上一点,且 ,试说明 .
(1)、若∠EAD=60°,求∠DFE的度数;(2)、若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.23. 红星商场购进A,B两种型号空调,A型空调每台进价为m元,B型空调每台进价为n元,5月份购进5台A型空调和7台B型空调共43000元;6月份购进7台A型空调和6台B型空调共45000元.(1)、求m,n的值;(2)、7月份该商场计划购进这两种型号空调共78000元,其中B型空调的数量不少于12台,试问有哪几种进货方案?24. 已知x,y同时满足x+3y=4﹣a,x﹣5y=3a.(1)、当a=4时,求x﹣y的值;(2)、试说明对于任意给定的数a,x+y的值始终不变;(3)、若y>1﹣m,3x﹣5≥m,且x只能取两个整数,求m的取值范围.25. 阅读理解:如图1,在 ABC中,D是BC边上一点,且 ,试说明 .解:过点A作BC边上的高AH,
∵ , ,
∴ ,
又∵ ,
∴ .
根据以上结论解决下列问题:如图2,在 ABC中,D是AB边上一点,且CD⊥AB,将 ACD沿直线AC翻折得到 ACE,点D的对应点为E,AE,BC的延长线交于点F,AB=12,AF=10.
 (1)、若CD=4,求 ACF的面积;(2)、设△ABF的面积为m,点P,M分别在线段AC,AF上.
(1)、若CD=4,求 ACF的面积;(2)、设△ABF的面积为m,点P,M分别在线段AC,AF上.①求PF+PM的最小值(用含m的代数式表示);
②已知 ,当PF+PM取得最小值时,求四边形PCFM的面积(用含m的代数式表示).