福建省莆田市涵江区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{16}$ 的平方根是（　　）

A、±4 B、4 C、±2 D、2

查看试题解析
2. 如图，点A、C、B在同一直线上，DC⊥EC，若∠BCD＝40°，则∠ACE的度数是（）

A、30° B、40° C、50° D、60°

查看试题解析
3. 下面说法不正确的是（）

A、1的平方根是±1 B、-1的算术平方根是-1 C、0平方根是0 D、-1的立方根是-1

查看试题解析
4. 若y轴上的点P到x轴的距离为3，则点P的坐标是（）

A、（3，0） B、（0，3） C、（3，0）或（﹣3，0） D、（0，3）或（0，﹣3）

查看试题解析
5. 如果∠A和∠B的两边分别平行，那么∠A和∠B的关系是（）

A、相等 B、互余或互补 C、互补 D、相等或互补

查看试题解析
6. 若 $m > n$ ，则下列不等式一定成立的是（）

A、 $2 m < 3 n$ B、 $2 + m > 2 + n$ C、 $2 - m > 2 - n$ D、 $\frac{m}{2} < \frac{n}{2}$

查看试题解析
7. 估计2 $\sqrt{13}$ ﹣2的值介于下列哪两个整数之间（）

A、2和3 B、3和4 C、4和5 D、5和6

查看试题解析
8. 在新冠肺炎防控期间，要了解某学校以下情况，其中适合用普查的有（）
①了解学校口罩、洗手液、消毒片的储备情况；

②了解全体师生在寒假期间的离锡情况；

③了解全体师生入校时的体温情况；

④了解全体师生对“七步洗手法”的运用情况.

A、1个 B、2个 C、3个 D、4

查看试题解析
9. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是关于x、y的二元一次方程组 ${\begin{array}{l} 3 x + n y = 8 \\ m x - y = 2 \end{array}$ 的解，则m+2n的值为（）

A、 $- \frac{5}{2}$ B、1 C、7 D、11

查看试题解析
10. 若不等式组 ${\begin{array}{l} x < 1 \\ x \geq m - 1 \end{array}$ 恰有两个整数解，则 $m$ 的取值范围是（）.

A、 $- 1 < m \leq 0$ B、 $- 1 \leq m < 0$ C、 $- 1 \leq m \leq 0$ D、 $- 1 < m < 0$

查看试题解析

二、填空题

11. 如图，要使AD//BF，则需要添加的条件是（写一个即可）.

查看试题解析
12. 已知点P在第二象限，点P到x轴的距离是2，到y轴的距离是3，那么点P的坐标是

查看试题解析
13. 如果 $\sqrt{a}$ 的平方根是 $\pm 3$ ，则 $a =$

查看试题解析
14. 如图是某公园里一处矩形风景欣赏区ABCD，长AB=50米，宽BC=30米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为米.

查看试题解析
15. 下列命题中，其逆命题成立的是.（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a²+b²=c² ，那么这个三角形是直角三角形.

查看试题解析
16. 不等式组 ${\begin{array}{l} - x + 2 < x - 6 \\ x > m \end{array}$ 的解集是 $x > 4$ ，那么 $m$ 的取值范围是．

查看试题解析

三、解答题

17. 计算： $| - 5 | + \sqrt{16} - 3^{2}$ .

查看试题解析
18. 解方程组： ${\begin{array}{l} 2 x - 5 y = - 3 \\ - 4 x + y = - 3 \end{array}$

查看试题解析
19. 解不等式： $3 (x + 1) \leq 5 x + 7$ ，并把它的解集在数轴上表示出来．

查看试题解析
20. 如图，已知∠ABC=∠BCD，∠ABC+∠CDG=180°，求证：BC∥GD.

查看试题解析
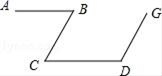21. 已知方程组 ${\begin{matrix} x + y = - 7 + a \\ x - y = 1 + 3 a \end{matrix}$ 的解x为非正数，y为负数.

(1)、求a的取值范围；

(2)、当a为何整数时，不等式2ax+x＞2a+1的解集为x＜1？

查看试题解析
22. 在平面直角坐标系xOy中，点A（1，1），B（3，2），将点A向左平移两个单位，再向上平移4个单位得到点C.

(1)、写出点C坐标；

(2)、求△ABC的面积.

查看试题解析
23. 某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算（小数部分无条件舍去） .

(1)、下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，

(2)、若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？

查看试题解析
24. 如图，在平面直角坐标系中，已知A，B，C三点的坐标分别为（0，a）（b，0）（b，c）（如图所示），其中a，b，c满足关系式（a﹣2）²+ $\sqrt{b - 3}$ =0，|c﹣4|≤0.

(1)、求a，b，c的值；

(2)、如果在第二象限内有一点P（m，1），请用含m的代数式表示△AOP的面积；

(3)、在（2）的条件下，是否存在点P，使△AOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析
25. 如图，取一副三角板按图1拼接，固定三角板ADE（∠AED＝30°的Rt $△$ ），将三角板ABC（∠ACB＝45°的Rt $△$ ）绕点A顺时针旋转一个大小为α的角（0°＜c≤45°），试问：

(1)、当α＝度时，能使图2中的AB∥DE；

(2)、当α＝度时，能使图3中的AB与AE重合；

(3)、当0°＜a≤45°时，连接BD（如图12﹣4），探求∠DBC+∠CAE+∠BDE的值的大小变化情况，并说明理由.

查看试题解析