福建省宁德市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 计算： $2^{- 1} =$ （）

A、2 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 在下列四所大学的校标中，内圆部分的图案不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.数据0.000000022用科学记数法表示为（）

A、 $0.22 \times 10^{- 7}$ B、 $2.2 \times 10^{- 8}$ C、 $2.2 \times 10^{- 9}$ D、 $22 \times 10^{- 10}$

查看试题解析
4. 下列四个图形中， $∠ 1 = ∠ 2$ 一定成立的是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是（）

A、 $a^{5} \cdot a^{2} = a^{10}$ B、 $2 a + a = 3 a^{2}$ C、 ${(3 a^{3})}^{2} = 6 a^{6}$ D、 $a^{6} \div a^{3} = a^{3}$

查看试题解析
6. 现有长度分别为 $3 cm$ 和 $5 cm$ 的两根木棒，若从下列长度的木棒中选择一根与原有的两根木棒首尾相接围成一个三角形，则这根木棒长度可以是（）

A、 $2 cm$ B、 $3 cm$ C、 $8 cm$ D、 $9 cm$

查看试题解析
7. 如图，由两个完全相同的三角板拼成一个四边形，则下列条件能直接判断 $A D // B C$ 的是（）

A、 $∠ A D B = ∠ C B D$ B、 $∠ A B D = ∠ C D B$ C、 $∠ B A D = ∠ D C B$ D、 $∠ B A D + ∠ C D A = 180 °$

查看试题解析
8. 同时抛两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1~6的点数，则下列事件中是不可能事件的是（）

A、点数之和为奇数 B、点数之和等于1 C、点数之和为偶数 D、点数之和大于9

查看试题解析

9. 一个学习小组利用同一块木板，测量了小车从不同高度下滑的时间，得到如表所示的一组数据：

支撑物的高度 $h$ （ $cm$ ）	10	20	30	40	50	60	70	80	90	100
小车下滑的时间 $t$ （ $s$ ）	4.23	3.00	2.45	2.13	1.89	1.71	1.59	1.50	1.41	1.35

若支撑物的高度 $h$ 为 $75 cm$ ，则小车下滑的时间最有可能的是（）

A、

1.57 s

B、

1.55 s

C、

1.54 s

D、

1.51 s

查看试题解析

10. 如图，已知 $△ A B C$ ， $B A = B C$ ，点 $D$ 是 $B C$ 上一点.尺规作图：过点 $D$ 作 $∠ C D E = ∠ B$ ， $D E$ 交 $A C$ 于点 $E$ ：以点 $E$ 为圆心， $E A$ 长为半径作弧，交 $A B$ 于点 $F$ ，连接 $E F$ .若 $∠ D E F = x °$ ， $∠ B = y °$ ，则 $y$ 与 $x$ 的关系式是（）

A、 $y = \frac{1}{2} x$ B、 $y = - \frac{1}{2} (180 - x)$ C、 $y = 90 - x$ D、 $y = 180 - 2 x$

查看试题解析

二、填空题

11. 若 $∠ A$ 的余角等于35°，则 $∠ A =$ °.

查看试题解析
12. 计算(x+2)(x-2)=.

查看试题解析
13. 在如图所示的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为．

查看试题解析
14. 如图， $A D$ 是 $△ A B C$ 的高， $C E$ 是 $△ A D C$ 角平分线.若 $∠ B A D = ∠ E C D$ ， $∠ B = 70 °$ ，则 $∠ C A D =$ °.

查看试题解析
15. 如图是一个数值转换器，若输入的数是2021，则输出的数是.

查看试题解析
16. 在如图所示的网格图中，每个小正方形的边长都为1.沿着图中的虚线，可以将该图形分割成2个全等的图形.在所有的分割方案中，最长分割线的长度等于.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(x + 1)}^{2} - x (x + 1)$ ；

(2)、 $(x - y) (x - 2 y) + (3 x^{3} y - 6 x y^{3}) \div 3 x y$ ，其中 $x = 2$ ， $y = - 3$ .

查看试题解析
18. 请将下面的说理过程和理由补充完整.
已知：如图， $A B // D E$ ， $A B = D E$ ， $B C = E F$ .说明 $A C // D F$ 的理由.

解： $∵ A B // D E$ ，

$∴ ∠ B =$ _▲_.（      ）

在 $△ A B C$ 和 $△ D E F$ 中， ${\begin{array}{l} A B = D E \\ ∠ B = ∠ E \\ B C = E F \end{array}$ .

$∴ △ A B C ≌ △ D E F$ .（      ）

$∴ ∠ A C B = ∠ D F E$ .（      ）

$∵ ∠ A C B + ∠ A C F = 180 °$ ， $∠ D F E + ∠ D F C = 180 °$ ，

$∴ ∠ A C F =$ _▲_.（等角的补角相等）

$∴ A C // D F$ .（      ）

查看试题解析
19. 为迎接建党100周年，某公司开展重走红军路活动，组织员工徒步前往某老区基点村.队伍从公司出发，行进一段后停下休息，随后再继续前进到达目的地.队伍行进的路程 $s$ （千米）与时间 $t$ （时）的关系如图所示，请根据图中提供的信息回答下列问题：

(1)、公司到该老区基点村的路程是千米，队伍中途休息了小时；

(2)、图中点 $A$ 表示的实际意义是什么？

(3)、队伍休息前的行进速度快还是休息后的速度快？每小时快多少千米？

查看试题解析
20. 如图， $A B$ ， $C D$ 交于点 $O$ ， $A C = D B$ ， $∠ A C D = ∠ D B A$ .

(1)、说明 $△ A O C ≌ △ D O B$ 的理由；

(2)、若 $∠ A C D = 94 °$ ， $∠ C A O = 28 °$ ，求 $∠ O C B$ 的度数.

查看试题解析
21. 如图，七边形 $A B C D E F G$ 是正七边形.

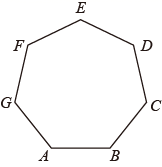(1)、若从点 $C$ ， $D$ ， $E$ ， $F$ ， $G$ 中任取一点，以所取点及点 $A$ ， $B$ 为顶点画三角形，求该三角形是等腰三角形的概率.

(2)、请仅用无刻度的直尺画出该七边形的一条对称轴 $l$ ，使点 $A$ 与点 $B$ 关于直线 $l$ 对称.

查看试题解析
22. 图1是由边长分别为 $a$ ， $b$ 的两个正方形拼成的图形，其面积为 $S_{1}$ ；图2是长、宽分别为 $a$ ， $b$ 的长方形，其面积为 $S_{2}$ .

(1)、图3是由图1中的图形补成的大正方形，其面积为 $S_{3}$ ，则 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 的数量关系是；

(2)、在图1边长为 $a$ 的正方形中放入两个边长为 $b$ 的小正方形，得到图4所示的图形.若 $S_{1} = 13$ ， $S_{2} = 5$ ，求图4中阴影部分的面积.

查看试题解析
23. 在 $△ A B C$ 中，若最大内角是最小内角的 $n$ 倍（ $n$ 为大于1的整数），则称 $△ A B C$ 为 $n$ 倍角三角形.例如：在 $△ A B C$ 中， $∠ A = 20 °$ ， $∠ B = 40 °$ ， $∠ C = 120 °$ ，则称 $△ A B C$ 为6倍角三角形.

(1)、在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ B = 60 °$ ，则 $△ A B C$ 为倍角三角形；

(2)、若一个等腰三角形是4倍角三角形，求最小内角的度数；

(3)、如图，点 $E$ 在 $D F$ 上， $B E$ 交 $A D$ 于点 $C$ ， $A B = A D$ ， $∠ B A D = ∠ E A F$ ， $∠ B = ∠ D = 25 °$ ， $∠ F = 75 °$ .找出图中所有的 $n$ 倍角三角形，并写出它是几倍角三角形.

查看试题解析