福建省南平市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最大的是（）

A、0 B、 $\sqrt{2}$ C、－3 D、 $- \sqrt{5}$

查看试题解析
2. 在平面直角坐标系中，点(1,-2)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列调查中，适宜采用全面调查的是（）

A、对宇宙飞船零部件质量的调查 B、了解春节联欢晚会的收视率 C、对本市七年级学生周末写作业时间的调查 D、鞋厂检测生产的鞋底能承受的弯折次数

查看试题解析
4. 已知 ${\begin{matrix} x = 1 \\ y = 1 \end{matrix}$ 是关于x，y的二元一次方程 $2 x - y = a$ 的解，那么a的值为（）

A、1 B、－1 C、2 D、－2

查看试题解析
5. 一元一次不等式 $3 x > - 3$ 的解集是（）

A、 $x > 1$ B、 $x > - 1$ C、 $x < 1$ D、 $x < - 1$

查看试题解析
6. 如图，估计 $\sqrt{10}$ 的值所对应的点可能落在（）

A、点A处 B、点B处 C、点C处 D、点D处

查看试题解析
7. 若 $a < b$ ，则下列不等式正确的是（）

A、 $a + 1 > b + 1$ B、 $- 2 a < - 2 b$ C、 $3 a < 3 b$ D、 $a - 3 > b - 3$

查看试题解析
8. 如图，点E在DA的延长线上，下列条件中不能判断AB $/ /$ DC的是（）

A、 $∠ E A B = ∠ D$ B、 $∠ B A C = ∠ A C D$ C、 $∠ B + ∠ B C D = 180 °$ D、 $∠ B = ∠ E A B$

查看试题解析
9. 《九章算术》中有一道“盈不足术”问题，原文为：今有人共买物，人出八，盈三；人出七，不足四，问人数，物价各几何?译文为：现有一些人共同购买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？这个物品的价格是多少？设共同购买该物品的有x人，该物品的价格是y元，则根据题意，列出的方程组为（）

A、 ${\begin{array}{l} 8 x - y = - 3 \\ 7 x - y = 4 \end{array}$ B、 ${\begin{array}{l} 8 y - x = 3 \\ 7 y - x = 4 \end{array}$ C、 ${\begin{array}{l} 8 y - x = - 3 \\ 7 y - x = - 4 \end{array}$ D、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = - 4 \end{array}$

查看试题解析
10. 已知 ${\begin{array}{l} x + 2 y = 3 k \\ 2 x + y = k + 1 \end{array}$ ，且 $0 < x - y < 1$ ，则k的取值范围为（）

A、 $\frac{1}{2} < k < 1$ B、 $0 < k < \frac{1}{2}$ C、 $0 < k < 1$ D、 $- 1 < k < - \frac{1}{2}$

查看试题解析

二、填空题

11. 若 $m^{2} = 9$ ，则m=.

查看试题解析
12. 如图，直线 $A B$ 与 $C D$ 相交于点O，若 $∠ A O C + ∠ B O D = 80 °$ ，则 $∠ A O C =$ 度.

查看试题解析
13. 把方程 $y - x = 3$ 改写成用含x的式子表示y的形式，则y =.

查看试题解析
14. 若点 $P (a - 2 ， 0)$ 在y轴上，则a的值为.

查看试题解析
15. 为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数.请根据统计表计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为.

1分钟内跳绳的次数

人数

40≤x＜80

10

80≤x＜120

50

120≤x＜160

30

160≤x＜200

10

查看试题解析
16. 一组按规律排列的多项式： $a + b$ ， $a^{2} - b^{3}$ ， $a^{3} + b^{5}$ ， $a^{4} - b^{7}$ ，……，其中第2021个式子是.

查看试题解析

三、解答题

17. 计算： $\sqrt{4} - \sqrt[3]{27} + | 1 - \sqrt{2} |$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 (x - 3) < x - 4 \\ x - 2 < 3 x \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析
19. 如图，三角形ABC（记作 $△$ ABC）三个顶点的坐标分别是A（－2，1），B（－3，－2），C（1，－2），先将 $△$ $A B C$ 向上平移3个单位长度，再向右平移2个单位长度，得到 $△$ $A_{1} B_{1} C_{1}$ .

(1)、在图中画出 $△$ $A_{1} B_{1} C_{1}$ ；

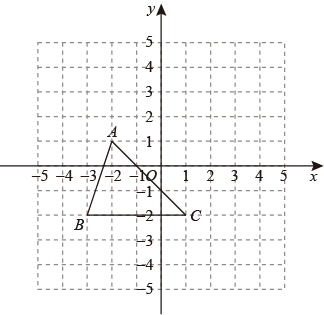(2)、若点P在x轴上运动，当线段PA长度最小时，点P的坐标为，依据是.

(3)、若y轴有一点Q，使 $△$ QBC与 $△$ ABC面积相等，求出Q点的坐标.

查看试题解析
20. 我市为响应国家“低碳环保，绿色出行”的号召，投放“共享单车”供市民出行时租用.寒假期间，七年级数学兴趣小组对某投放点的租车情况进行一周的调查，并把收集的数据绘制成下面的频数分布直方图和扇形统计图：

(1)、根据统计图提供的信息，估算这个站点一周的租车总次数是多少次；

(2)、补全频数分布直方图；

(3)、求周三租车次数所在扇形的圆心角度数.

查看试题解析
21. 疫情防控期间，学校准备购买甲、乙两种洗手液，已知购买2瓶甲种洗手液和3瓶乙种洗手液共需90元；购买1瓶甲种洗手液和2瓶乙种洗手液共需55元.

(1)、求甲、乙两种洗手液每瓶各需多少元？

(2)、如果学校要购买甲、乙两种洗手液共30瓶，且总费用不超过527元，求至少要购买甲种洗手液多少瓶？

查看试题解析
22. 如图，已知AD⊥BC于点D，EF⊥BC于点F，若∠E＝∠3.求证：AD平分∠BAC.（请完成下面的证明，并填上对应的推理根据）
证明：∵AD⊥BC于点D，EF⊥BC于点F（已知），

∴∠ADB＝∠EFB＝90°（                ），

∴AD∥EF（                ），

∴∠1＝∠E（                ），

∠2＝∠3（                ）.

又 ∵∠E＝∠3（已知），

∴∠1＝∠2（                ），

∴AD平分∠BAC（                ）.

查看试题解析
23. 将一付三角尺 $△$ ACO与 $△$ BOD如图放置在平面直角坐标系中，点O与坐标原点重合，点B，C在x轴的正半轴上，点D在y轴的负半轴上，∠ACO=90°，∠A=30°，∠OBD=45°.

(1)、已知 $△$ ACO的面积为 $\frac{3}{2} \sqrt{3}$ （平方单位）， $O C = \sqrt{3}$ ，求点A的坐标；

(2)、将 $△$ ACO向下平移，使得点A与点C重合，得到 $△$ CNM，若MC与BD交于点P，则 $∠ D P M$ 的度数为；

(3)、点E在AC边上，将 $△$ AOE沿直线OE折叠得到 $△$ FOE，使得 $B D ⊥ O F$ ，求∠AOE的大小.

查看试题解析

1分钟内跳绳的次数	人数
40≤x＜80	10
80≤x＜120	50
120≤x＜160	30
160≤x＜200	10