福建省龙岩市新罗区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-20 类型:期末考试
一、单选题
-
1. 下列数中,是无理数的是( )A、 B、0 C、 D、2. 在平面直角坐标系中,下列各点位于第二象限的是( )A、 B、 C、 D、3. 下列各图中, 和 是对顶角的是( )A、
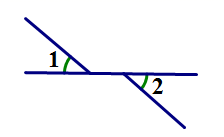 B、
B、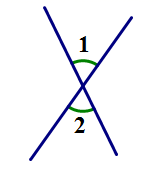 C、
C、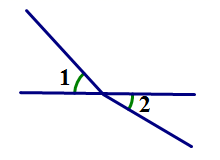 D、
D、 4. 如果 ,那么下列不等式成立的是( )A、 B、 C、 D、5. 下列命题中是真命题的是( )A、内错角相等 B、平行于同一条直线的两条直线互相平行 C、互补的两个角是邻补角 D、带根号的数一定是无理数6. 一个等腰直角三角板和一把直尺按如图所示的位置摆放,若 ,则 的度数是( )
4. 如果 ,那么下列不等式成立的是( )A、 B、 C、 D、5. 下列命题中是真命题的是( )A、内错角相等 B、平行于同一条直线的两条直线互相平行 C、互补的两个角是邻补角 D、带根号的数一定是无理数6. 一个等腰直角三角板和一把直尺按如图所示的位置摆放,若 ,则 的度数是( )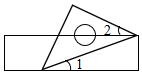 A、 B、 C、 D、7. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据, 年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法错误的是( )
A、 B、 C、 D、7. 党的十八大以来,党中央把脱贫攻坚摆到更加突出的位置,根据国家统计局发布的数据, 年年末全国农村贫困人口的情况如图所示,根据图中提供的信息,下列说法错误的是( ) A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务8. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、9. 在平面直角坐标系中,将 沿着 的正方向向右平移 个单位后得到 点.有四个点 、 、 、 ,一定在线段 上的是( )A、点 B、点 C、点 D、点10. 小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由小到大的顺序是( )A、小明、小亮、小华、小英 B、小明、小亮、小英、小华 C、小英、小华、小亮、小明 D、小亮、小英、小华、小明
A、2019年末,农村贫困人口比上年末减少551万人 B、2012年末至2019年末,农村贫困人口累计减少超过9000万人 C、2012年末至2019年末,连续7年每年农村贫困人口减少1000万人以上 D、为在2020年末农村贫困人口全部脱贫,今年要确保完成减少551万农村人口的任务8. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.其中一道题,原文是:“今三人共车,两车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、9. 在平面直角坐标系中,将 沿着 的正方向向右平移 个单位后得到 点.有四个点 、 、 、 ,一定在线段 上的是( )A、点 B、点 C、点 D、点10. 小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由小到大的顺序是( )A、小明、小亮、小华、小英 B、小明、小亮、小英、小华 C、小英、小华、小亮、小明 D、小亮、小英、小华、小明二、填空题
-
11. 计算 的值为;12. 如图,请填写一个条件,使结论成立:∵ , ∴ .
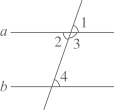 13. 把命题:“直角都相等”改写成“如果……那么……”的形式为.14. 已经点P 在平面直角坐标系的第四象限,则 的取值范围是.15. 小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是120千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区200户居民这一天投放的可回收垃圾共约千克.
13. 把命题:“直角都相等”改写成“如果……那么……”的形式为.14. 已经点P 在平面直角坐标系的第四象限,则 的取值范围是.15. 小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该小区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是120千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区200户居民这一天投放的可回收垃圾共约千克.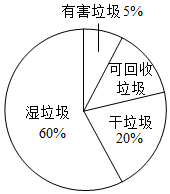 16. 已知关于x、y的方程组 ,其中 ,给出下列结论:
16. 已知关于x、y的方程组 ,其中 ,给出下列结论:① 是方程组的解;
②若 ,则 ;
③若 .则M的最小值为 ;
④若 时,则 ;
其中正确的有.(填写序号)
三、解答题
-
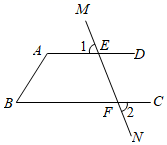
17. 计算:18. 解方程组:19. 解不等式组: 并写出它的所有整数解.20. 如图,已知: ,求 度数.
 21. 在正方形网格中建立平面直角坐标系 ,使得A,B两点的坐标分别为 ,过点B作 轴于点C.
21. 在正方形网格中建立平面直角坐标系 ,使得A,B两点的坐标分别为 ,过点B作 轴于点C.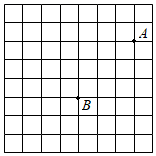 (1)、按照要求画出平面直角坐标系 ,写出点C的坐标__;(2)、计算以A,B,O为顶点的三角形的面积22. 七(3)班的生活委员第一学期为班级买了3个垃圾桶和5个拖把,共用了55元,第二学期买了4个垃圾桶和6个拖把,其中垃圾桶价格是第一学期价格的8折,拖把价格不变,共用了64元.求第一学期购买垃圾桶和拖把的单价分别是多少?23. 某区中小学开展“阳光体育”大课间活动,某校在大课间中开设了五项活动,A:体操,B:健美操,C:舞蹈,D:球类,E:跑步.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:
(1)、按照要求画出平面直角坐标系 ,写出点C的坐标__;(2)、计算以A,B,O为顶点的三角形的面积22. 七(3)班的生活委员第一学期为班级买了3个垃圾桶和5个拖把,共用了55元,第二学期买了4个垃圾桶和6个拖把,其中垃圾桶价格是第一学期价格的8折,拖把价格不变,共用了64元.求第一学期购买垃圾桶和拖把的单价分别是多少?23. 某区中小学开展“阳光体育”大课间活动,某校在大课间中开设了五项活动,A:体操,B:健美操,C:舞蹈,D:球类,E:跑步.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题: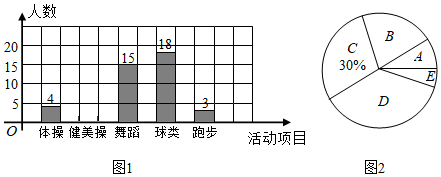 (1)、请将统计图1补充完整;(2)、统计图2中D项目对应的扇形的圆心角是几度(保留一位小数)?(3)、已知该校共有学生1200人,请根据调查结果估计该校喜欢球类的学生人数.24. 某竹凉席厂日产量为m条凉席,但随着夏季的到来,订单任务大幅增加,该厂经常无法完成当天的订单任务,需要将超出的订单任务交给第三方企业处理.已知该厂生产竹凉席,每天需固定费用300元,并且每生产1条竹凉席还需材料等费用80元;将订单任务给第三方企业处理,每条需支付120元.根据记录,5月26日,该厂完成订单任务25条竹凉席,费用共2580元.(1)、求该竹凉席厂日产量m;(2)、为控制生产成本,使得每天的平均费用不超过100元/条,试计算该厂一天能接受的订单任务范围.25. 在平面直角坐标系 中,把线段 先向右平移h个单位,再向下平移1个单位得到线段 (点A对应点C),其中 分别是第三象限与第二象限内的点.
(1)、请将统计图1补充完整;(2)、统计图2中D项目对应的扇形的圆心角是几度(保留一位小数)?(3)、已知该校共有学生1200人,请根据调查结果估计该校喜欢球类的学生人数.24. 某竹凉席厂日产量为m条凉席,但随着夏季的到来,订单任务大幅增加,该厂经常无法完成当天的订单任务,需要将超出的订单任务交给第三方企业处理.已知该厂生产竹凉席,每天需固定费用300元,并且每生产1条竹凉席还需材料等费用80元;将订单任务给第三方企业处理,每条需支付120元.根据记录,5月26日,该厂完成订单任务25条竹凉席,费用共2580元.(1)、求该竹凉席厂日产量m;(2)、为控制生产成本,使得每天的平均费用不超过100元/条,试计算该厂一天能接受的订单任务范围.25. 在平面直角坐标系 中,把线段 先向右平移h个单位,再向下平移1个单位得到线段 (点A对应点C),其中 分别是第三象限与第二象限内的点. (1)、若 ,求C点的坐标;(2)、若 ,连接 ,过点B作 的垂线l
(1)、若 ,求C点的坐标;(2)、若 ,连接 ,过点B作 的垂线l①判断直线l与x轴的位置关系,并说明理由;
②已知E是直线l上一点,连接 ,且 的最小值为1,若点B,D及点 都是关于x,y的二元一次方程 的解 为坐标的点,试判断 是正数、负数还是0?并说明理由.