重庆市沙坪坝区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元一次方程的是（）

A、 $x^{2} + 2 = 6$ B、 $x = 3$ C、 $x + y = 6$ D、 $\frac{2}{x} + 3 = 8$

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 不等式 $- 2 x \leq - 2$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如果一个三角形的两边长分别为3和6，那么第三边长可能是（）

A、1 B、3 C、7 D、9

查看试题解析
5. 下列各组数中，是方程 $2 x - y = 7$ 的解是的（）

A、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$

查看试题解析
6. 如图， $△ A B C ≌ △ D B E$ ， $∠ A B C = 80 °$ ， $∠ D = 65 °$ ，则 $∠ C$ 的度数为（）

A、20° B、25° C、30° D、35°

查看试题解析
7. 如果一个等腰三角形的一个外角为130°，那么顶角的度数为（）

A、50° B、80° C、130° D、50°或80°

查看试题解析
8. 某商品在进价的基础上提价20%后以96元的价格出售，则该商品的进价为（）

A、60元 B、70元 C、80元 D、86元

查看试题解析
9. 如图，已知 $a // b$ ， $△ A B O$ 是一直角三角板并按如图方式摆放，其中 $∠ A = 60 °$ ，将 $△ A B O$ 绕点O顺时针方向旋转45°，则 $∠ 1$ 的度数为（）

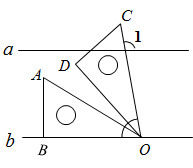A、95° B、105° C、120° D、135°

查看试题解析
10. 如图，图①用了1块墙砖铺成；图②用了3块墙砖铺成；图③用了6块墙砖铺成：……，按图中所示规律，图⑥所需墙砖数为（）

A、11 B、15 C、21 D、28

查看试题解析
11. 若关于 $x$ 的不等式组 ${\begin{array}{l} 2 x - a < 1 ， \\ x - 2 b > 3 \end{array}$ 的解集为 $- 1 < x < 1$ ，则 $(a + 1) (b - 1)$ 的值为（）

A、-6 B、6 C、-8 D、8

查看试题解析
12. 如图， $△ A B C$ 为等腰直角三角形， $∠ C = 90 °$ 、将 $△ A B C$ 按如图方式进行折叠，使点A与 $B C$ 边上的点F重合，折痕分别与 $A C$ 、 $A B$ 交于点D、点E.下列结论：① $∠ 1 = ∠ 2$ ；② $∠ 1 + ∠ 2 = 90 °$ ；③ $∠ 3 + ∠ B = 90 °$ ；④ $D F // A B$ .其中一定正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 方程 $\frac{1}{2} x = 1$ 的解为

查看试题解析
14. 已知 ${\begin{array}{l} x = a \\ y = b \end{array}$ ，是方程组 ${\begin{array}{l} x + 2 y = 8 \\ 2 x + y = 7 \end{array}$ 的解，则 $a - b$ 的值为.

查看试题解析
15. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
16. 如图， $△ A B C$ 中，点D、点E分别在边 $A B$ 、 $B C$ 上，连结 $A E$ 、 $D E$ ，若 $△ A D E ≌ △ B D E$ ， $A C ： A B ： B C = 2 ： 3 ： 4$ ，且 $△ A B C$ 的周长比 $△ A E C$ 的周长大6.则 $△ A E C$ 的周长为

查看试题解析
17. 关于y的方程 $1 - 2 y + a = - 3 (y - 1)$ 的解为正数，关于x的不等式组 ${\begin{array}{l} x \leq \frac{x + 3}{2} \\ 11 x - 5 > 2 a \end{array}$ 有且只有三个整数解，则符合条件的所有整数a的和为.

查看试题解析
18. 端午节有吃粽子的习惯，某商店购进肉粽、蛋黄粽、豆沙粽的数量之比为 $9 ： 15 ： 2$ .为促进销售，将全部粽子包装成A、B、C三种礼盒.礼盒A有2个肉粽、4个蛋黄粽；礼盒B有1个肉粽、3个蛋黄粽、1个豆沙粽；礼盒C有4个肉粽、2个豆沙粽.则礼盒A、礼盒B、礼盒C的盒数之比为.

查看试题解析

三、解答题

19. 解下列方程（组）：

(1)、 $4 x + 3 = 2 (x - 1) + 1$

(2)、 ${\begin{array}{l} x - 2 y = 3 ， \\ 2 x + y = 1. \end{array}$

查看试题解析
20. 解下列不等式（组）：

(1)、 $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1$

(2)、 ${\begin{array}{l} 2 x - 1 > - 2 + x ， \\ 3 x + 2 > 4 x \end{array}$

查看试题解析
21. 如图，格点 $△ A B C$ 在边长为1个单位长度的小正方形组成的网格中.

（ 1 ）请画出 $△ A B C$ 向右平移3个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）请画出 $△ A B C$ 关于点O成中心对称的 $△ A_{2} B_{2} C_{2}$ ；

（ 3 ）四边形 $A_{1} B_{1} A_{2} B_{2}$ 的面积为 .

查看试题解析
22. 已知方程组 ${\begin{matrix} 3 x + 2 y = m + 2 \\ 2 x + 3 y = m \end{matrix}$ 的解 $x ， y$ 互为相反数，求m的值，并求此方程组的解.

查看试题解析
23. 如图，在 $△ A B C$ 中，点D在 $A C$ 上， $∠ B D C$ 的平分线交 $B C$ 于点E，过点A作 $D E$ 的平行线交 $B C$ 于点F，交 $B D$ 于点 $G$ .

(1)、若 $∠ 1 = 30 °$ ， $∠ 2 = 80 °$ ，求 $∠ C$ 的度数；

(2)、若 $∠ B D C = 2 ∠ A B C$ ，请说明 $∠ 4 = ∠ 5 + 2 ∠ 3$ .

查看试题解析
24. 在“一带一路”建设中，中国水稻专家将“杂交水稻之父”袁隆平院士的水稻培育技术带到了非洲.在我国专家驻地附近的A村有稻田100亩，B村有稻田200亩，在技术指导前A、B两村的水稻总产量仅80吨.经过我国专家的指导后，现在A村的水稻平均亩产量比原来提高了50%，B村的水稻平均亩产量比原来提高了40%，A、B两村的水稻总产量共114吨.

(1)、请分别求出原来A、B两村水稻的平均亩产量：

(2)、经过我国专家技术指导之后，A村的水稻出米率为80%，且A、B两村的水稻加工后大米的总重量不低于82.8吨，那么B村的水稻出米率至少为多少？（注：出米率=加工后大米的重量 $\div$ 加工前水稻的重量）

查看试题解析
25. 三个自然数x、y、z组成一个有序数组 $(x ， y ， z)$ ，如果满足 $x - y = y - z$ ，那么我们称数组 $(x ， y ， z)$ 为“蹦蹦数组”.例如：数组 $(2 ， 5 ， 8)$ 中 $2 - 5 = 5 - 8$ ，故 $(2 ， 5 ， 8)$ 是“蹦蹦数组”；数组 $(4 ， 6 ， 12)$ 中 $4 - 6 \neq 6 - 12$ ，故 $(4 ， 6 ， 12)$ 不是“蹦蹦数组”.

(1)、分别判断数组 $(437 ， 307 ， 177)$ 和 $(601 ， 473 ， 346)$ 是否为“蹦蹦数组”；

(2)、s和t均是三位数的自然数，其中s的十位数字是3，个位数字是2，t的百位数字是2，十位数字是5，且 $s - t = 274$ .是否存在一个整数b，使得数组 $(s ， b ， t)$ 为“蹦蹦数组”.若存在，求出b的值；若不存在，请说明理由；

(3)、有一个三位数的自然数，百位数字是1，十位数字是p，个位数字是q，若数组 $(1 ， p ， q)$ 为“蹦蹦数组”，且该三位数是7的倍数，求这个三位数.

查看试题解析
26. 如图，在 $△ A B C$ 中，点D在边 $A C$ 上， $∠ A B D = 90 °$ .将 $△ B C D$ 沿 $B D$ 对折得到 $△ B E D$ ， $B E$ 交 $A C$ 于点F.

(1)、如图①，若 $∠ A = 40 °$ ， $∠ C = 30 °$ ，求 $∠ A F B$ 的度数；

(2)、如图②，若 $∠ 1 = ∠ 2$ ，请说明 $∠ 4 = 4 ∠ 3$ ；

(3)、若 $∠ A = 40 °$ ，将 $△ B E D$ 绕点B逆时针方向旋转一个角度 $α (0 < α < 180 °)$ ，记旋转中的 $△ B E D$ 为 $△ B D_{1} E_{1}$ .在旋转过程中，直线 $D_{1} E_{1}$ 分别与直线 $A B$ 、直线 $A C$ 交于点M、点N，是否存在这样的点M、点N，使 $∠ A M N$ 与 $∠ A N M$ 相等？若存在，请直接写出旋转角 $α$ 的度数；若不存在，请说明理由.

查看试题解析