重庆市南岸区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-20 类型：期末考试

进入出卷网下载

一、单选题

1. 将一张长方形纸对折，然后用笔尖在上面扎出“M”，再把它铺平，你见到的图形可能是（）

A、 B、 C、 D、

查看试题解析
2. 下列成语或词语所反映的事件中，可能性大小最小的是（）

A、瓜熟蒂落 B、守株待兔 C、旭日东升 D、夕阳西下

查看试题解析
3. 如图， $m // n$ ，其中 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $130 °$ B、 $140 °$ C、 $150 °$ D、 $160 °$

查看试题解析
4. 下列计算正确的是（）

A、 ${(2 x^{2})}^{3} = 8 x^{5}$ B、 ${(2 x^{2})}^{3} = 6 x^{5}$ C、 ${(2 x^{2})}^{3} = 6 x^{6}$ D、 ${(2 x^{2})}^{3} = 8 x^{6}$

查看试题解析
5. 如图所示， $Δ A B C$ 的边 $A C$ 上的高是（）

A、线段 $A E$ B、线段 $B A$ C、线段 $B D$ D、线段 $D A$

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ B = 50 °$ ， $C D$ 平分 $∠ A C B$ ，则 $∠ A D C$ 的度数是（）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
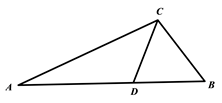7. 已知 $(x - 5) (x + a) = x^{2} + b x - 15$ ，则b的值是（）

A、-5 B、-2 C、2 D、3

查看试题解析
8. 如图，通过尺规作图，得到 $△ C O D ≌ △ C^{'} O^{'} D^{'}$ ，再利用全等三角形的性质，得到了 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ ，那么，根据尺规作图得到 $△ C O D ≌ △ C^{'} O^{'} D^{'}$ 的理由是（）

A、 $S A S$ B、 $A A S$ C、 $S S S$ D、 $A S A$

查看试题解析
9. 利用图形中面积的等量关系可以得到某些数学公式．例如，根据图甲，我们可以得到两数和的平方公式：（a+b）²＝a²+2ab+b² ．你根据图乙能得到的数学公式是（）

A、（a+b）（a﹣b）＝a²﹣b² B、（a﹣b）²＝a²﹣2ab+b² C、a（a+b）＝a²+ab D、a（a﹣b）＝a²﹣ab

查看试题解析
10.
如图，△ABC的面积为6，AC=3，现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C′处，P为直线AD上的一点，则线段BP的长不可能是（　　）

A、3 B、4 C、5.5 D、10

查看试题解析
11. 如图，在 $△ A B C$ 中，点D是 $B C$ 边上的中点.连接 $A D$ ，点E是 $A D$ 的中点，连接 $C E$ ，点F是 $C E$ 的中点.若 $S_{△ D E F} = 2$ ，则 $S_{△ A B C}$ 等于（）

A、16 B、14 C、12 D、10

查看试题解析
12. 如图，在 $△ A B C$ 中，AB＝AC，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点.若BC＝4， $△ A B C$ 面积为10，则BM+MD长度的最小值为（）

A、 $\frac{5}{2}$ B、3 C、4 D、5

查看试题解析

二、填空题

13. 计算： $2 x^{2} \cdot x =$ .

查看试题解析
14. 已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为

查看试题解析
15. 新学期开学，刚刚组建的七年级（1）班有男生30人，女生24人，欲从该班级中选出一名值日班长，任何人都有同样的机会，则这班选中一名男生当值日班长的概率是．

查看试题解析
16. 如图，平移图形M，与图形N可以拼成一个平行四边形，则图中α的度数是°.

查看试题解析
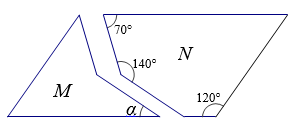17. 若长方形的周长为20，其中一边长为 $x (x > 0)$ ，面积为y，则y与x之间的关系式为.

查看试题解析
18. 定义：若一个正整数能表示为两个连续自然数的平方差，那么就称这个正整数为“平方差数”.例如： $1 = 1^{2} - 0^{2} ， 3 = 2^{2} - 1^{2} ， 5 = 3^{2} - 2^{2}$ ，因此1，3，5这三个数都是“平方差数”.则不大于200的所有“平方差数”之和为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(a + b)}^{2} + a (a - 2 b)$ ；

(2)、 $(12 a^{3} - 9 a^{2} + 3 a) \div 3 a$ .

查看试题解析
20. 如图，已知 $A B / / C D$ ， $A B = C D$ ， $B E = C F$ .

求证：

(1)、 $Δ A B F ≅ Δ D C E$ ；

(2)、 $A F / / D E$ .

查看试题解析
21. 如图，已知 $△ A B C$ .

(1)、作 $∠ A B C$ 的平分线，交边 $A C$ 于点D；作 $B C$ 的垂直平分线，交 $B C$ 于点E，交 $A B$ 于点F，连接 $D F$ ；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在（1）所作的图中，连接 $C F$ .如果 $D F // C B$ ，猜想并说明 $∠ B C F$ 与 $∠ B D F$ 存在的数量关系.

查看试题解析
22. 已有两根长度分别为 $4 c m$ 和 $5 c m$ 的线段，同时，在一旁有7根长度不等的线段，这些线段的长度分别与相应的卡片正面上标注的线段长一致.这7张卡片的背面完全相同，卡片正面上分别标注了 $3 c m$ 、 $4 c m$ 、 $4 c m$ 、 $5 c m$ 、 $6 c m$ 、 $7 c m$ 、 $7 c m$ .把这7张卡片背面朝上，从中随机抽取一张卡片，以卡片上标注的数据对应的线段作为第三条线段的长度，回答以下问题：

(1)、判断事件“从中抽取的长度能够与 $4 c m$ 和 $5 c m$ 组成等边三角形”是什么事件，并写出其发生的概率；

(2)、求抽取出的卡片上标注的数据对应的线段能够与 $4 c m$ 和 $5 c m$ 的线段组成等腰三角形的概率；

(3)、小兰和小英打算以取出一张卡片上标注的数据对应的线段能够与 $4 c m$ 和 $5 c m$ 组成三角形的周长的奇偶性作为游戏规则.三角形周长为奇数小兰胜，三角形周长为偶数小英胜，请问游戏公平吗？若公平，请说明理由；若不公平，请重新设计一个公平的规则.

查看试题解析
23. 阅读思考：我们知道：
$15^{2} = 225 = 1 \times (1 + 1) \times 100 + 5 \times 5$ ；

$32 \times 38 = 1216 = 3 \times (3 + 1) \times 100 + 2 \times 8$ ；

$74 \times 76 = 5624 = 7 \times (7 + 1) \times 100 + 4 \times 6$ ；

$66 \times 64 = 4224 = 6 \times (6 + 1) \times 100 + 6 \times 4$ .

观察以上等式，可以发现，两个两位数相乘，若它们的十位数字相同，个位数字之和为10，可以先用这两个两位数的十位数字乘以比它们十位数字大1的数，并把所得的结果乘以100；再加上这两个两位数个位数字相乘的积，所得的结果就是这两个两位数相乘的积.

解决问题：

(1)、请用观察到的规律直接写出：
① $37 \times 33$ ；

② $95 \times 95$ ；

(2)、十位数字为a，个位数字分别为m，n的两个两位数相乘，则这两个两位数可以分别表示为 $10 a + m ， 10 a + n$ .如果 $m + n = 10$ ，上述规律可表示为 $(10 a + m) (10 a + n) = 100 a (a + 1) + m n$ ，请说明这个等式成立的合理性；

(3)、个位数字为c，十位数字分别为a，b的两个两位数相乘，如果 $a + b = 10$ ，请仿照（2）写出其规律等式，并说明这个等式成立的合理性.

查看试题解析
24. 甲、乙两地的路程为 $300km$ ，一辆汽车早上8：00从甲地出发，匀速向乙地行驶，途中休息一段时间后，按原速继续前进.设汽车出发 $x h$ 后离甲地的路程为 $y km$ ，图中折线 $O - C - D - E$ 表示y与x之间的函数关系.

(1)、根据图象，直接写出休息前汽车行驶的速度；

(2)、若线段 $D E$ 所表示的y与x之间的函数表达式为 $y = 80 x - 40$ ；当上午10点时，求汽车离开甲地的距离是多少 $km$ ？

(3)、上午11点接到通知，要求12点准时到达乙地，请问汽车仍按原速行驶能否准时到达？如果能，请算出到达的时间：如果不能，请求出速度提升为多少时，汽车能在12点准时到达乙地？

查看试题解析
25. 如图，已知 $∠ B A D = ∠ C A E = 90 ° ， A B = A D ， A E = A C$ .

(1)、 $△ A B C$ 与 $△ A D E$ 全等吗？请说明理由；

(2)、若 $A F ⊥ C B$ ，垂足为F，请说明线段 $2 C F = C E$ ；

(3)、在（2）的基础上，猜想线段 $B F ， D E ， C D$ 存在的数量关系，并直接写出结论.

查看试题解析
26. 要在一条笔直的公路l边上建一个快递配送点，方便为同侧的A，B两个居民小区发送快件.

(1)、试确定快递配送点P的位置，使它分别到A，B的两个居民小区的距离相等，请在如图中，画出点P的大致位置；

(2)、试确定快递配送点M的位置，使它到A，B的两个居民小区的距离之和最短.请在如图中画出点M的大致位置；

(3)、如图，D是 $△ A B C$ 内一点，连接 $B D ， D C$ .延长 $B D$ 交 $A C$ 于点E.
∵在 $△ D E C$ 中， $D E + E C > D C$ ①，

在 $△ A B E$ 中， $A B + A E > B D + D E$ ②；

∴①＋②得 $D E + E C + A B + A E > D C + B D + D E$ ；

∴ $A B + A C > B D + D C$ .

如果在A，B两个居民区之间规划一个正方形生态保护区，送快件的路线不能穿过该区域.请同学们用以上这个结论，在图中画出快递配送点Q的大致位置，使得它到两个居民小区路程之和最短.

查看试题解析