湖南省长沙市雅实、西雅、雅洋2020-2021学年八年级上学期数学第一次月考试卷

试卷更新日期：2021-08-20 类型：月考试卷

进入出卷网下载

一、单选题

1. 若 $a$ 的相反数是 $- 3$ ，则 $a$ 的值为（）

A、1 B、2 C、3 D、-3

查看试题解析
2. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（　　）

A、 B、 C、 D、

查看试题解析
3. 新型冠状病毒肺炎是一种急性感染性肺炎，其病原体是一种先前未在人类中发现的新型冠状病毒，即2019新型冠状病毒.截止到2020年9月21日5时38分，全球新冠肺炎累计确诊病例突破3118万例.把3118万例用科学记数法表示为（）例.

A、31.18×10⁶ B、0.3118×10⁸ C、3.118×10⁸ D、3.118×10⁷

查看试题解析
4. 下列计算不正确的是（）

A、 $\pm \sqrt{9} = \pm 3$ B、 $2 ab + 3 ba = 5 ab$ C、 $3 x - 2 x = 1$ D、 $| - 3 | = 3$

查看试题解析
5. 如果等腰三角形的两边长分别为2和5，则它的周长为( )

A、9 B、7 C、12 D、9或12

查看试题解析
6. 下列判断错误的是（）

A、等腰三角形是轴对称图形 B、有两条边相等的三角形是等腰三角形 C、等腰三角形的两个底角相等 D、等腰三角形的角平分线、中线、高互相重合

查看试题解析
7. 如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（）

A、15° B、30° C、45° D、60°

查看试题解析
8. 如图，在△ABC中，BC＝8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长等于（　　）

A、6cm B、8cm C、10cm D、12cm

查看试题解析
9. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，△ABC的面积为10，DE=2，AB=6，则AC的长是（）

A、4 B、3 C、6 D、5

查看试题解析
10. 等腰三角形一腰上的高与另一腰的夹角为 $25 °$ ，则其底角为（）

A、 $65 °$ B、 $32.5 °$ C、 $32.5 °$ 或 $57.5 °$ D、 $32.5 °$ 或 $65 °$

查看试题解析
11. 如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是（）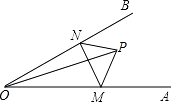

A、25° B、30° C、35° D、40°

查看试题解析
12. 如图，已知AD为△ABC的高线，AD=BC，以AB为底边作等腰Rt△ABE，且点E在△ABC内部，连接ED，EC，延长CE交AD于F点，下列结论：①△ADE≌△BCE，②CE⊥DE，③BD=AF，④ $S_{△ B D E} = S_{△ A C E}$ ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 多边形的每个外角都等于45°，则这个多边形是边形.

查看试题解析
14. 规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“雅系特征值”，记作k，若 $k = \frac{2}{3}$ ，则该等腰三角形的顶角为.

查看试题解析
15. 已知点A（-4，5）与点B（a，b）关于y轴对称，则a-b的值为.

查看试题解析
16. 如图，已知∠MON=30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上；△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形.若OA₁=1，则△A₂₀₁₅B₂₀₁₅A₂₀₁₆的边长为.

查看试题解析

三、解答题

17. 计算： $- 1^{2} - | \sqrt{2} - 2 | - \sqrt[3]{8} + \sqrt{4}$ .

查看试题解析
18. 解不等式组 ${\begin{matrix} 5 x + 1 > 3 （ x - 1 ） \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{matrix}$ ，并把它的解集在数轴上表示出来．

查看试题解析
19. 按要求用尺规作图（要求：不写作法，但要保留作图痕迹.）

(1)、已知：线段 $A B$
求作：线段 $A B$ 的垂直平分线 $M N$ .

(2)、已知： $∠ A O B$
求作： $∠ A O B$ 的角平分线 $O C$ .

查看试题解析
20. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (1 ， 1)$ ， $B (4 ， 2)$ ， $C (3 ， 4)$ .

(1)、①请画出 $△ A B C$ 向左平移5个单位长度后得到的 $Δ A_{1} B_{1} C_{1}$ ；
②请画出 $△ A B C$ 关于x轴对称的 $△ A_{2} B_{2} C_{2}$ ；

(2)、请求出 $△ A B C$ 的面积.

(3)、请在y轴上找一点P，使得PA+PC最小.

查看试题解析
21. 2020年3月，中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》长沙市教育局发布了“普通中小学校劳动教育状况评价指标”，为了解某校学生一周劳动次数的情况，随机抽取若干学生进行调查，得到如下统计图表：

(1)、这次调查活动共抽取人；

(2)、m= ， n= .

(3)、请将条形图补充完整

(4)、若该校学生总人数为3000人，根据调查结果，请你估计该校一周劳动4次及以上的学生人数.

查看试题解析
22. 我市创全国卫生城市，梅溪湖社区积极响应，决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱，若购买4个垃圾箱比购买5个温馨提示牌多350元，垃圾箱的单价是温馨提示牌单价的3倍.

(1)、求温馨提示牌和垃圾箱的单价各是多少元？

(2)、如果该街道需购买温馨提示牌和垃圾箱共3000个.该街道计划费用不超过35万元，而且垃圾箱的个数不少于温馨提示牌的个数的1.5倍，求有几种可供选择的方案？并找出资金最少的方案，求出最少需多少元？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D，E，F分别在 $A B ， B C ， A C$ 边上，且 $B E = C F$ ， $B D = C E$ .

(1)、求证： $△ D E F$ 是等腰三角形；

(2)、求证： $∠ B = ∠ D E F$ ；

(3)、当 $∠ A = 40 °$ 时，求 $∠ D E F$ 的度数.

查看试题解析
24. 对于平面直角坐标系 xOy中的点P（a，b），若点 $P^{'}$ 的坐标为 $(a + \frac{b}{k} ， k a + b)$ （其中k为常数，且 $k \neq 0$ ），则称点 $P^{'}$ 为点P的“k之雅礼点”.例如：P（1，4）的“2之雅礼点”为 $P^{'} (1 + \frac{4}{2} ， 2 \times 1 + 4)$ ，即 $P^{'}$ （3，6）.

(1)、①点P（-1，-3）的“3之雅礼点” $P^{'}$ 的坐标为；
②若点P的“k之雅礼点” $P^{'}$ 的坐标为（2，2），请写出一个符合条件的点P的坐标；

(2)、若点P在x轴的正半轴上，点P的“k之雅礼点”为 $P^{'}$ 点，且 $△ O P P^{'}$ 为等腰直角三角形，则k的值为；

(3)、在（2）的条件下，若关于x的方程 $k x + m x = m n + 2$ 有无数个解，求 $m 、 n$ 的值.

查看试题解析
25. 如图1， $Δ A C B$ 为等腰三角形， $∠ A B C = 90^{\circ}$ ，点 $P$ 在线段 $B C$ 上（不与 $B 、 C$ 重合），以 $A P$ 为腰长作等腰直角 $Δ P A Q$ ， $Q E ⊥ A B$ 于 $E$ .

(1)、求证： $Δ P A B ≅ A Q E$ ；

(2)、连接 $C Q$ 交 $A B$ 于 $M$ ，若 $P C = 2 P B$ ，求 $\frac{P C}{M B}$ 的值.

(3)、如图2，过 $Q$ 作 $Q F ⊥ A Q$ 于 $A B$ 的延长线于点 $F$ ，过 $P$ 点作 $D P ⊥ A P$ 交 $A C$ 于 $D$ ，连接 $D F$ ，当点 $P$ 在线段 $B C$ 上运动时（不与 $B ， C$ 重合），式子 $\frac{Q F - D P}{D F}$ 的值会变化吗？若不变，求出该值；若变化，请说明理由..

查看试题解析