湖南省常德市澧县第二教育联组2020-2021学年九年级上学期数学10月联考试卷
试卷更新日期:2021-08-20 类型:月考试卷
一、单选题
-
1. 已知函数 的图象过点 ,那么下列四个点中,也在这个函数图象上的是( )A、 B、 C、 D、2. 在反比例函数 的图象在某象限内y随着x的增大而增大,则m的取值范围是( )A、 B、 C、 D、3. 关于x的方程 是一元二次方程,则 的取值范围是( )A、 B、 C、 且 D、 且4. 如图,矩形ABCD的面积为3,反比例函数 的图象过点A,则 的值( )
 A、6 B、3 C、-3 D、-65. 反比例函数 图象上有三个点 ,其中 ,则 的大小关系是 ( )A、 B、 C、 D、6. 若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是 ,则另一个交点的坐标是( )A、 B、 C、 D、7. 如图,在同一平面直角坐标系中,反比例函数 与一次函数y=kx−1(k为常数,且k≠0)的图象可能是( )A、
A、6 B、3 C、-3 D、-65. 反比例函数 图象上有三个点 ,其中 ,则 的大小关系是 ( )A、 B、 C、 D、6. 若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是 ,则另一个交点的坐标是( )A、 B、 C、 D、7. 如图,在同一平面直角坐标系中,反比例函数 与一次函数y=kx−1(k为常数,且k≠0)的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )
8. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )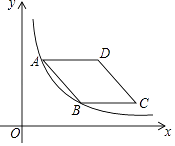 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2二、填空题
-
9. 若反比例函数 的图象在第二、四象限,则m的值是.10. 已知反比例函数 ,当 时,y的取值范围是.11. 已知关于x的方程 是一元二次方程,则m的值为.12. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是 .13. 某超市一月份的营业额为220万元,一月、二月、三月的营业额共1000万元,如果设平均每月增长率为 ,则依题意列方程为.14. 如图,某农场有一块长为40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2 , 则小路的宽为.
 15. 已知 是方程 的两个实数根,则代数式 .16. 将 代入反比例函数 中,所得函数值记为 ,又将 代入原反比例函数中,所得函数值记为 ,再将 代入原反比例函数中,所得函数值记为 ,…,如此继续下去,则 .
15. 已知 是方程 的两个实数根,则代数式 .16. 将 代入反比例函数 中,所得函数值记为 ,又将 代入原反比例函数中,所得函数值记为 ,再将 代入原反比例函数中,所得函数值记为 ,…,如此继续下去,则 .三、解答题
-
17. 用适当的方法解方程.(1)、 ;(2)、18. 若代数式 ,请比较 的大小.19. 现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.(1)、求该快递公司投递总件数的月平均增长率;
(2)、如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?20. 已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)、证明:不论m为何值时,方程总有实数根;(2)、m为何整数时,方程有两个不相等的正整数根.21. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .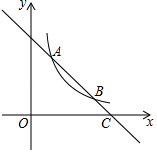 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.22. 如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5m,墙外可用宽度为3.25m.现有长为21m的篱笆,计划靠着院墙围成一个中间有一道隔栏的长方形花圃.
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.22. 如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5m,墙外可用宽度为3.25m.现有长为21m的篱笆,计划靠着院墙围成一个中间有一道隔栏的长方形花圃. (1)、若要围成总面积为36m2的花圃,边AB的长应是多少?(2)、花圃的面积能否达到36.75m2?若能,求出边AB的长;若不能,请说明理由.23. 已知A(-2n,n)、B(n,-4)两点是一次函数 和反比例函数 图象的两个交点.
(1)、若要围成总面积为36m2的花圃,边AB的长应是多少?(2)、花圃的面积能否达到36.75m2?若能,求出边AB的长;若不能,请说明理由.23. 已知A(-2n,n)、B(n,-4)两点是一次函数 和反比例函数 图象的两个交点. (1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,写出不等式 的解集.24. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种海产品的销售情况,请解答以下问题:(1)、当销售单价定为每千克55元时,月销售量是千克,月销售利润是元;(2)、设销售单价为每千克x元,月销售利润为y,请你求出y与x之间的函数关系式;(3)、商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应该定为多少元?25. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积;(3)、观察图象,写出不等式 的解集.24. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种海产品的销售情况,请解答以下问题:(1)、当销售单价定为每千克55元时,月销售量是千克,月销售利润是元;(2)、设销售单价为每千克x元,月销售利润为y,请你求出y与x之间的函数关系式;(3)、商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应该定为多少元?25. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题: (1)、药物燃烧时与药物燃烧后,y关于x的函数关系式.(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过几分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?26. 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发。
(1)、药物燃烧时与药物燃烧后,y关于x的函数关系式.(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过几分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?26. 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发。 (1)、几秒钟后,P、Q间的距离等于4 cm?(2)、几秒种后,△BPQ的面积与四边形CQPA的面积相等?
(1)、几秒钟后,P、Q间的距离等于4 cm?(2)、几秒种后,△BPQ的面积与四边形CQPA的面积相等?