江苏省泰州市兴化市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-20 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 的半径为 ,点 到圆心 的距离为 ,点 与 的位置关系是( )A、点 在 内 B、点 在 上 C、点 在 外 D、无法确定3. 正方形、菱形、矩形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分一组对角4. 已知 是分式方程 的解,那么实数 的值为( )A、3 B、4 C、5 D、65. 下列一元二次方程中,有两个不相等的实数根的是( )A、 B、 C、 D、6. 下列有关反比例函数 的结论中错误的有( )个
①图象分别位于第一、三象限;②当 时, 随 的增大而减小;③点 在它的图象上,则点 也在它的图象上;④当 时, .
A、1 B、2 C、3 D、4二、填空题
-
7. 若二次根式 有意义,则x的取值范围是 .8. 当 时,分式 值为0.9. 如图,在⊙O中, ,∠A=30°,则∠B=°.
 10. 若函数 的图象在每个象限内 的值随 值的增大而增大,则 的取值范围为.11. 某工厂经过两年的时间将某种产品的产量从每年14400台提高到16900台.设平均每年增长的百分率为 ,可得方程.12. 若 、 是两个连续的整数,且 ,则 .13. 小明要把一篇文章录入电脑,所需时间 与录入文字的速度 (字 )之间的反比例函数关系如图所示,如果小明要在 内完成录入任务,则小明录入文字的速度至少为字 .
10. 若函数 的图象在每个象限内 的值随 值的增大而增大,则 的取值范围为.11. 某工厂经过两年的时间将某种产品的产量从每年14400台提高到16900台.设平均每年增长的百分率为 ,可得方程.12. 若 、 是两个连续的整数,且 ,则 .13. 小明要把一篇文章录入电脑,所需时间 与录入文字的速度 (字 )之间的反比例函数关系如图所示,如果小明要在 内完成录入任务,则小明录入文字的速度至少为字 .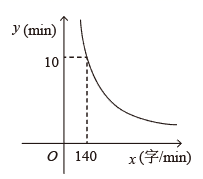 14. 若点 , , 都在反比例函数 的图象上,则 、 、 的大小关系是.(用“<”连接)15. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.
14. 若点 , , 都在反比例函数 的图象上,则 、 、 的大小关系是.(用“<”连接)15. 如图, 的直径 ,弦 ,垂足为 , ,则 的长为.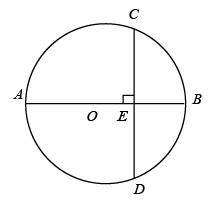 16. 如图,正方形 的边长为6, 是 的中点, 是等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,则 的值为.
16. 如图,正方形 的边长为6, 是 的中点, 是等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,则 的值为.
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解方程:(1)、 ;(2)、 .19. 先化简再求值: ,其中 .20. 某商店经销的某种商品,每件成本为40元.经市场调研,售价为50元时,可销售200件;售价每增加 元,销售量将减少10件.如果这种商品全部销售完,那么该商店可盈利2000元.问:该商店销售了这种商品多少件?每件售价多少元?21. 已知:如图,矩形 的对角线 、 相交于点 , , .
 (1)、若 , ,求 的长;(2)、求证:四边形 是菱形.22. 如图,函数 与 的图象相交于点 , .
(1)、若 , ,求 的长;(2)、求证:四边形 是菱形.22. 如图,函数 与 的图象相交于点 , . (1)、结合图象,直接写出不等式 的解集:;(2)、求 和 的值;(3)、连接 、 ,求 的面积.23. 已知关于 的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两个实数根为 , ,且 ,求 的值.24. 如图1,在四边形 中, 、 、 、 分别是 、 、 、 的中点.
(1)、结合图象,直接写出不等式 的解集:;(2)、求 和 的值;(3)、连接 、 ,求 的面积.23. 已知关于 的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两个实数根为 , ,且 ,求 的值.24. 如图1,在四边形 中, 、 、 、 分别是 、 、 、 的中点.
 (1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.25. 阅读下面的材料,解决问题
(1)、求证:四边形 是平行四边形;(2)、如图2,延长 、 相交于点 ,连接 、 、 ,若 ,求四边形 的面积.25. 阅读下面的材料,解决问题像 、 、 ……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如, 和 、 与 、 与 等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.我们把通过适当的变形化去分母中根号的运算叫做分母有理化.
例如: ; ;
(1)、计算: ;(2)、计算: ;(3)、比较 和 的大小,并说明理由;(4)、计算: .26. 已知:如图1,函数 和 的图象相交于点 和点 .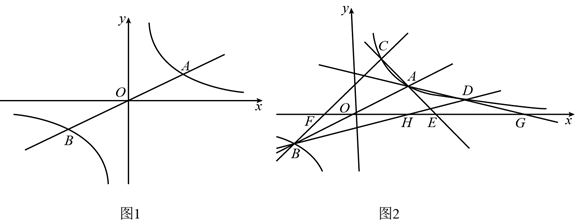 (1)、求点 和点 的坐标(用含 的式子表示);(2)、如图2,点 的坐标为 ,点 是第一象限内函数 的图象上的动点,且在点 的右侧,直线 、 、 、 分别与 轴相交于点 、 、 、 .
(1)、求点 和点 的坐标(用含 的式子表示);(2)、如图2,点 的坐标为 ,点 是第一象限内函数 的图象上的动点,且在点 的右侧,直线 、 、 、 分别与 轴相交于点 、 、 、 .①判定 的形状,并说明理由;
②点 在运动的过程中, 和 的度数和是否变化?如果变化,说明理由;如果不变,求出 和 的度数和.