四川省宜宾市2021年中考数学试卷
试卷更新日期:2021-08-20 类型:中考真卷
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、-22. 下列图形是轴对称图形的是( )A、
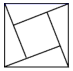 B、
B、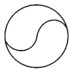 C、
C、 D、
D、 3. 2021年宜宾市中考人数已突破64000人,数据64000用科学记数法表示为( )A、 B、 C、 D、4. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、85. 一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )
3. 2021年宜宾市中考人数已突破64000人,数据64000用科学记数法表示为( )A、 B、 C、 D、4. 若长度分别是a、3、5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、4 D、85. 一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )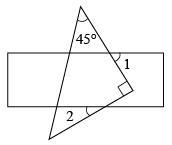 A、30° B、35° C、40° D、45°6. 下列运算正确的是( )A、 B、 C、 D、7. 下列说法正确的是( )A、平行四边形是轴对称图形 B、平行四边形的邻边相等 C、平行四边形的对角线互相垂直 D、平行四边形的对角线互相平分8. 若关于x的分式方程 有增根,则m的值是( )A、1 B、﹣1 C、2 D、﹣29. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A、30° B、35° C、40° D、45°6. 下列运算正确的是( )A、 B、 C、 D、7. 下列说法正确的是( )A、平行四边形是轴对称图形 B、平行四边形的邻边相等 C、平行四边形的对角线互相垂直 D、平行四边形的对角线互相平分8. 若关于x的分式方程 有增根,则m的值是( )A、1 B、﹣1 C、2 D、﹣29. 如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( ) A、 B、2 C、 D、10. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、1211. 在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( )
A、 B、2 C、 D、10. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、1211. 在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( ) A、27 B、42 C、55 D、21012. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( )
A、27 B、42 C、55 D、21012. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( ) A、2 B、 C、 D、3
A、2 B、 C、 D、3二、填空题
-
13. 不等式2x﹣1>1的解集是.14. 分解因式: .15. 从甲、乙、丙三人中选一人参加环保知识决赛,经过两轮测试,他们的平均成绩都是88.9,方差分别是 ,你认为最适合参加决赛的选手是(填“甲”或“乙”或“丙”).16. 据统计,2021年第一季度宜宾市实现地区生产总值约652亿元,若使该市第三季度实现地区生产总值960亿元,设该市第二、三季度地区生产总值平均增长率为x,则可列方程.17. 如图,⊙O的直径AB=4,P为⊙O上的动点,连结AP,Q为AP的中点,若点P在圆上运动一周,则点Q经过的路径长是.
 18. 如图,在矩形ABCD中,AD= AB,对角线相交于点O,动点M从点B向点A运动(到点A即停止),点N是AD上一动点,且满足∠MON=90°,连结MN.在点M、N运动过程中,则以下结论中,①点M、N的运动速度不相等;②存在某一时刻使 ;③ 逐渐减小;④ .正确的是.(写出所有正确结论的序号)
18. 如图,在矩形ABCD中,AD= AB,对角线相交于点O,动点M从点B向点A运动(到点A即停止),点N是AD上一动点,且满足∠MON=90°,连结MN.在点M、N运动过程中,则以下结论中,①点M、N的运动速度不相等;②存在某一时刻使 ;③ 逐渐减小;④ .正确的是.(写出所有正确结论的序号)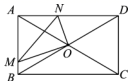
三、解答题
-
19.(1)、计算: ;(2)、化简: .20. 如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
 21. 为帮助学生养成热爱美、发现美的艺术素养,某校开展了“一人一艺”的艺术选修课活动.学生根据自己的喜好选择一门艺术项目(A:书法,B:绘画,C:摄影,D:泥塑,E:剪纸),张老师随机对该校部分学生的选课情况进行调查后,制成了两幅不完整的统计图(如图所示).
21. 为帮助学生养成热爱美、发现美的艺术素养,某校开展了“一人一艺”的艺术选修课活动.学生根据自己的喜好选择一门艺术项目(A:书法,B:绘画,C:摄影,D:泥塑,E:剪纸),张老师随机对该校部分学生的选课情况进行调查后,制成了两幅不完整的统计图(如图所示). (1)、张老师调查的学生人数是.(2)、若该校共有学生1000名,请估计有多少名学生选修泥塑;(3)、现有4名学生,其中2人选修书法,1人选修绘画,1人选修摄影,张老师要从这4人中任选2人了解他们对艺术选修课的看法,请用画树状图或列表的方法,求所选2人都是选修书法的概率.22. 全国历史文化名城宜宾有许多名胜古迹,始建于明朝的白塔是其中之一.如图,为了测量白塔的高度AB,在C处测得塔顶A的仰角为45°,再向白塔方向前进15米到达D处,又测得塔顶A的仰角为60°,点B、D、C在同一水平线上,求白塔的高度AB.( ≈1.7,精确到1米)
(1)、张老师调查的学生人数是.(2)、若该校共有学生1000名,请估计有多少名学生选修泥塑;(3)、现有4名学生,其中2人选修书法,1人选修绘画,1人选修摄影,张老师要从这4人中任选2人了解他们对艺术选修课的看法,请用画树状图或列表的方法,求所选2人都是选修书法的概率.22. 全国历史文化名城宜宾有许多名胜古迹,始建于明朝的白塔是其中之一.如图,为了测量白塔的高度AB,在C处测得塔顶A的仰角为45°,再向白塔方向前进15米到达D处,又测得塔顶A的仰角为60°,点B、D、C在同一水平线上,求白塔的高度AB.( ≈1.7,精确到1米)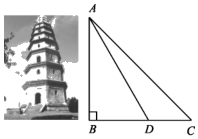 23. 如图,一次函数y=ax+b的图象与反比例函数 的图象交于点A、B,与x轴交于点 ,若OC=AC,且 =10
23. 如图,一次函数y=ax+b的图象与反比例函数 的图象交于点A、B,与x轴交于点 ,若OC=AC,且 =10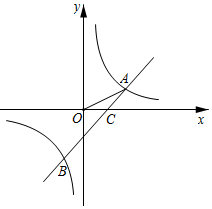 (1)、求反比例函数与一次函数的表达式;(2)、请直接写出不等式ax+b> 的解集.24. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求反比例函数与一次函数的表达式;(2)、请直接写出不等式ax+b> 的解集.24. 如图1,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.25. 如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若tan∠ADC= ,AC=2,求⊙O的半径;(3)、如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连结BE.求sin∠DBE的值.25. 如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE. (1)、求抛物线的表达式;(2)、判断△BCE的形状,并说明理由;(3)、如图2,以C为圆心, 为半径作⊙C,在⊙C上是否存在点P,使得BP+ EP的值最小,若存在,请求出最小值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、判断△BCE的形状,并说明理由;(3)、如图2,以C为圆心, 为半径作⊙C,在⊙C上是否存在点P,使得BP+ EP的值最小,若存在,请求出最小值;若不存在,请说明理由.