江苏省常州市2021年中考数学试卷
试卷更新日期:2021-08-20 类型:中考真卷
一、单选题
-
1. 的倒数是( )
A、2 B、﹣2 C、 D、﹣2. 计算 的结果是( )A、 B、 C、 D、3. 如图是某几何体的三视图,该几何体是( )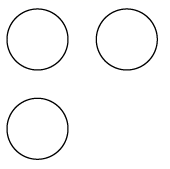 A、正方体 B、圆锥 C、圆柱 D、球4. 观察所示脸谱图案,下列说法正确的是( )
A、正方体 B、圆锥 C、圆柱 D、球4. 观察所示脸谱图案,下列说法正确的是( ) A、它是轴对称图形,不是中心对称图形 B、它是中心对称图形,不是轴对称图形 C、它既是轴对称图形,也是中心对称图形 D、它既不是轴对称图形,也不是中心对称图形5. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( )
A、它是轴对称图形,不是中心对称图形 B、它是中心对称图形,不是轴对称图形 C、它既是轴对称图形,也是中心对称图形 D、它既不是轴对称图形,也不是中心对称图形5. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( )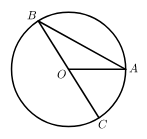 A、 B、 C、 D、6. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、
A、 B、 C、 D、6. 以下转盘分别被分成2个、4个、5个、6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是 ,则对应的转盘是( )A、 B、
B、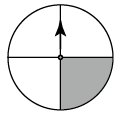 C、
C、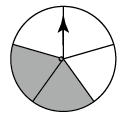 D、
D、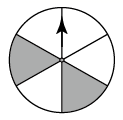 7. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、8. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )
7. 已知二次函数 ,当 时,y随x增大而增大,则实数a的取值范围是( )A、 B、 C、 D、8. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )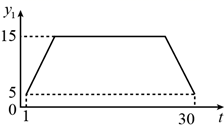 A、
A、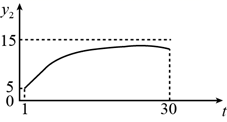 B、
B、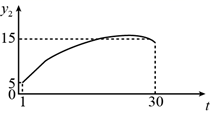 C、
C、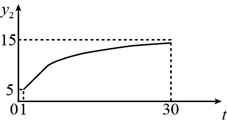 D、
D、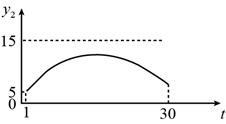
二、填空题
-
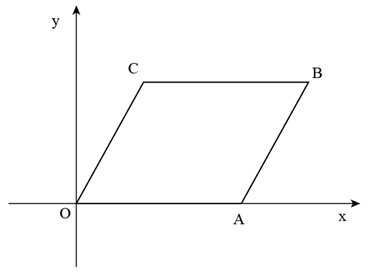
9. 计算: .10. 计算: .11. 分解因式: .12. 近年来,5G在全球发展迅猛,中国成为这一领域基础设施建设、技术与应用落地的一大推动者.截至2021年3月底,中国已建成约819000座5G基站,占全球70%以上.数据819000用科学记数法表示为.13. 数轴上的点A、B分别表示 、2,则点离原点的距离较近(填“A”或“B”).14. 如图,在平面直角坐标系 中,四边形 是平行四边形,其中点A在x轴正半轴上.若 ,则点A的坐标是.
 15. 如图,在 中,点D、E分别在 、 上, .若 ,则 .
15. 如图,在 中,点D、E分别在 、 上, .若 ,则 .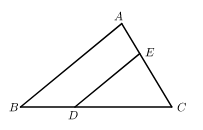 16. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点D、E,连接 ,过点A作 ,垂足为F,将 分割后拼接成矩形 .若 ,则 的面积是.
16. 中国古代数学家刘徽在《九章算术注》中,给出了证明三角形面积公式的出入相补法.如图所示,在 中,分别取 、 的中点D、E,连接 ,过点A作 ,垂足为F,将 分割后拼接成矩形 .若 ,则 的面积是. 17. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 .
17. 如图,在 中, ,点D、E分别在 、 上,点F在 内.若四边形 是边长为1的正方形,则 . 18. 如图,在 中, ,D是 上一点(点D与点A不重合).若在 的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点,则 长的取值范围是.
18. 如图,在 中, ,D是 上一点(点D与点A不重合).若在 的直角边上存在4个不同的点分别和点A、D成为直角三角形的三个顶点,则 长的取值范围是.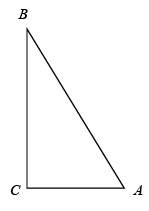
三、解答题
-
19. 计算: .20. 解方程组和不等式组:(1)、(2)、21. 为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如下统计图.
 (1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该小区有居民2000人,请估计该小区对垃圾分类知识“完全了解”的居民人数.22. 在3张相同的小纸条上,分别写上条件:①四边形 是菱形;②四边形 有一个内角是直角;③四边形 的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.(1)、搅匀后从中任意抽出1支签,抽到条件①的概率是;(2)、搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形 同时满足抽到的2张小纸条上的条件,求四边形 一定是正方形的概率.23. 如图,B、F、C、E是直线l上的四点, .
(1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该小区有居民2000人,请估计该小区对垃圾分类知识“完全了解”的居民人数.22. 在3张相同的小纸条上,分别写上条件:①四边形 是菱形;②四边形 有一个内角是直角;③四边形 的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.(1)、搅匀后从中任意抽出1支签,抽到条件①的概率是;(2)、搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形 同时满足抽到的2张小纸条上的条件,求四边形 一定是正方形的概率.23. 如图,B、F、C、E是直线l上的四点, . (1)、求证: ;(2)、将 沿直线l翻折得到 .
(1)、求证: ;(2)、将 沿直线l翻折得到 .①用直尺和圆规在图中作出 (保留作图痕迹,不要求写作法);
②连接 ,则直线 与l的位置关系是▲ .
24. 为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天,该景点在设施改造后平均每天用水多少吨?25. 如图,在平面直角坐标系 中,一次函数 的图象分别与x轴、y轴交于点A、B,与反比例函数 的图象交于点C,连接 .已知点 , . (1)、求b、k的值;(2)、求 的面积.26. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.
(1)、求b、k的值;(2)、求 的面积.26. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.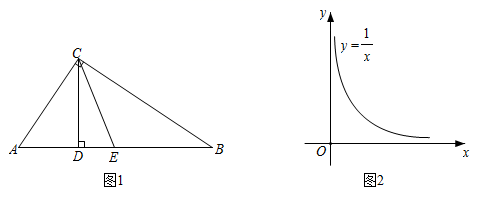 (1)、【理解】
(1)、【理解】
如图1, ,垂足分别为C、D,E是 的中点,连接 .已知 , .①分别求线段 、 的长(用含a、b的代数式表示);
②比较大小: ▲ (填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(2)、【应用】
如图2,在平面直角坐标系 中,点M、N在反比例函数 的图象上,横坐标分别为m、n.设 ,记 .①当 时, ▲ ;当 时, ▲ ;
②通过归纳猜想,可得l的最小值是 ▲ .请利用图2构造恰当的图形,并说明你的猜想成立.
27. 在平面直角坐标系 中,对于A、 两点,若在y轴上存在点T,使得 ,且 ,则称A、 两点互相关联,把其中一个点叫做另一个点的关联点.已知点 、 ,点 在一次函数 的图象上.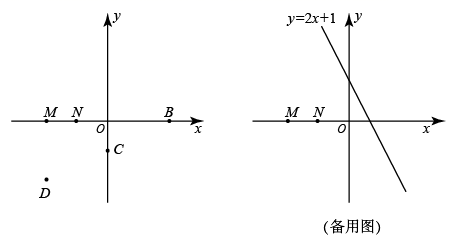 (1)、①如图,在点 、 、 中,点M的关联点是(填“B”、“C”或“D”);
(1)、①如图,在点 、 、 中,点M的关联点是(填“B”、“C”或“D”);②若在线段 上存在点 的关联点 ,则点 的坐标是;
(2)、若在线段 上存在点Q的关联点 ,求实数m的取值范围;(3)、分别以点 、Q为圆心,1为半径作 、 .若对 上的任意一点G,在 上总存在点 ,使得G、 两点互相关联,请直接写出点Q的坐标.28. 如图,在平面直角坐标系 中,正比例函数 和二次函数 的图象都经过点 和点B,过点A作 的垂线交x轴于点C.D是线段 上一点(点D与点A、O、B不重合),E是射线 上一点,且 ,连接 ,过点D作x轴的垂线交抛物线于点F,以 、 为邻边作 .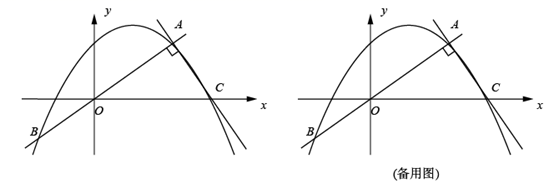 (1)、填空: , ;(2)、设点D的横坐标是 ,连接 .若 ,求t的值;(3)、过点F作 的垂线交线段 于点P.若 ,求 的长.
(1)、填空: , ;(2)、设点D的横坐标是 ,连接 .若 ,求t的值;(3)、过点F作 的垂线交线段 于点P.若 ,求 的长.