吉林省中考数学真题汇编(近三年)3 函数
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如图,在平面直角坐标系中,点A、B在函数 的图象上,x过点A作x轴的垂线,与函数 的图象交于点C , 连结BC交x轴于点D . 若点A的横坐标为1, ,则点B的横坐标为( )
 A、 B、 C、 D、2. 如图,在平面直角坐标系中,点A的坐标为 , 轴于点B,点C是线段 上的点,连结 .点P在线段 上,且 .函数 的图象经过点P.当点C在线段 上运动时,k的取值范围是( )
A、 B、 C、 D、2. 如图,在平面直角坐标系中,点A的坐标为 , 轴于点B,点C是线段 上的点,连结 .点P在线段 上,且 .函数 的图象经过点P.当点C在线段 上运动时,k的取值范围是( )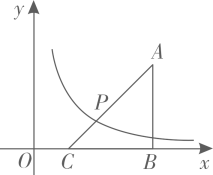 A、 B、 C、 D、3. 如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3)、(3,0)。∠ACB=90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为( )
A、 B、 C、 D、3. 如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,3)、(3,0)。∠ACB=90°,AC=2BC,函数y= (k>0,x>0)的图象经过点B,则k的值为( )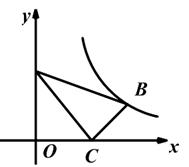
A、 B、9 C、 D、4. 如图,在平面直角坐标系中,O为坐标原点,P是函数y= (x>0)图像上的一点,过点P作x轴的垂线交函数y=- (x>0)的图像于点A,过点A作y轴的垂线交PO的延长线于点B。若点P从左向右运动,则△ABP的面积( ) A、逐渐变大 B、逐渐变小 C、保持不变,且面积为9 D、保持不变,且面积为185. 如图,在平面直角坐标系中,函数 的图象和 ABC都在第一象限, ,BC∥x轴,且BC =4,点A的坐标为(3,5).若将 ABC向下平移m(m>0)个单位,A、C两点的对应点同时落在函数 的图象上,则k的值为( )
A、逐渐变大 B、逐渐变小 C、保持不变,且面积为9 D、保持不变,且面积为185. 如图,在平面直角坐标系中,函数 的图象和 ABC都在第一象限, ,BC∥x轴,且BC =4,点A的坐标为(3,5).若将 ABC向下平移m(m>0)个单位,A、C两点的对应点同时落在函数 的图象上,则k的值为( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,线段AC的端点A在y轴正半轴上,AC∥x轴,点C在第一象限,函数y= (x>0)的图象交边AC于点B . D为x轴上一点,连结CD、BD . 若BC=2AB , 则△BCD的面积为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,线段AC的端点A在y轴正半轴上,AC∥x轴,点C在第一象限,函数y= (x>0)的图象交边AC于点B . D为x轴上一点,连结CD、BD . 若BC=2AB , 则△BCD的面积为( ) A、4 B、2 C、1 D、0.57. 如图,在平面直角坐标系,等腰直角 的顶点A、B均在函数 的图象上,点C在y轴正半轴上, ,若点A的横坐标为 ,点B的纵坐标为1,则k的值为( )
A、4 B、2 C、1 D、0.57. 如图,在平面直角坐标系,等腰直角 的顶点A、B均在函数 的图象上,点C在y轴正半轴上, ,若点A的横坐标为 ,点B的纵坐标为1,则k的值为( )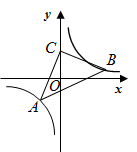 A、1 B、2 C、4 D、68. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )
A、1 B、2 C、4 D、68. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )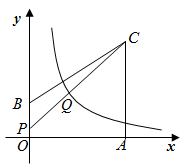 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在平面直角坐标系中,点 在抛物线 上,过点A作y轴的垂线,交抛物线于另一点B , 点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
 10. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .
10. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .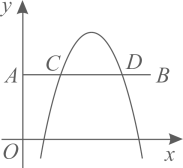 11. 如图,在平面直角坐标系中,抛物线y=ax2-2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M。P为抛物线的顶点。若直线OP交直线AM于点B,且M为线段AB的中点,则a的值。
11. 如图,在平面直角坐标系中,抛物线y=ax2-2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M。P为抛物线的顶点。若直线OP交直线AM于点B,且M为线段AB的中点,则a的值。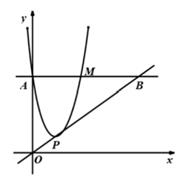 12. 在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是 .13. 已知抛物线 经过 , 两点.若 , 是抛物线上的两点,且 ,则 的取值范围是 .14. 如图,在平面直角坐标系中,O为坐标原点,抛物线y=a(x-2)2+3(a<0)的顶点为A,与抛物线y=ax2+3交于x轴上方的点B,过点B作垂直于y轴的直线,分别交两条抛物线于C,D两点(C,D两点均不与点B重合),连结AD,AC,CO,OD,则四边形ACOD的面积为
12. 在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是 .13. 已知抛物线 经过 , 两点.若 , 是抛物线上的两点,且 ,则 的取值范围是 .14. 如图,在平面直角坐标系中,O为坐标原点,抛物线y=a(x-2)2+3(a<0)的顶点为A,与抛物线y=ax2+3交于x轴上方的点B,过点B作垂直于y轴的直线,分别交两条抛物线于C,D两点(C,D两点均不与点B重合),连结AD,AC,CO,OD,则四边形ACOD的面积为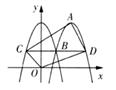 15. 如图,二次函数y= x2+4x+c的图象的顶点为A,与y轴的交点为B,BC∥x轴,交抛物线于点C,则△ABC的面积是
15. 如图,二次函数y= x2+4x+c的图象的顶点为A,与y轴的交点为B,BC∥x轴,交抛物线于点C,则△ABC的面积是
三、解答题
-
16. 小明要把一篇社会调查报告录入电脑,当他以100字/分钟的速度录入文字时,经过240分钟能完成录入。设他录入文字的速度为v字/分钟时,完成录入的时间为t分钟。求t与v之间的函数关系式(不必写出自变量的取值范围)。
四、综合题
-
17. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天)之间的关系如图所示.
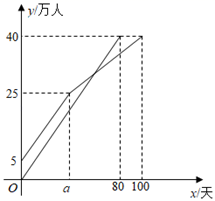 (1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.18. 如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
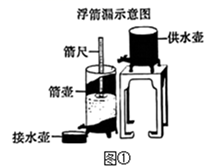
(1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.18. 如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .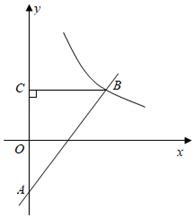 (1)、求反比例函数的解析式;(2)、求 的面积.19. 《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水查流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间,某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
(1)、求反比例函数的解析式;(2)、求 的面积.19. 《九章算术》中记载,浮箭漏(图①)出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水查流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间,某学校STEAM小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:(实验观察)实验小组通过观察,每2小时记录次箭尺读数,得到下表:
供水时间x(小时)
0
2
4
6
8
箭尺读数y(厘米)
6
18
30
42
54
 (1)、(探索发现)建立平面直角坐标系,如图②,横轴表示供水时间x . 纵轴表示箭尺读数y , 描出以表格中数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.(3)、(结论应用)应用上述发现的规律估算:
(1)、(探索发现)建立平面直角坐标系,如图②,横轴表示供水时间x . 纵轴表示箭尺读数y , 描出以表格中数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.(3)、(结论应用)应用上述发现的规律估算:供水时间达到12小时时,箭尺的读数为多少厘米?
(4)、如果本次实验记录的开始时间是上午8:00,那么当箭尺读数为90厘米时是几点钟?(箭尺最大读数为100厘米)20. 如图,在平面直角坐标系中,O为坐标原点,点A,B在函数 的图象上(点B的横坐标大于点A的横坐标),点A的坐示为 ,过点A作 轴于点D,过点B作 轴于点C,连接 , . (1)、求k的值.(2)、若D为 中点,求四边形 的面积.21. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.
(1)、求k的值.(2)、若D为 中点,求四边形 的面积.21. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.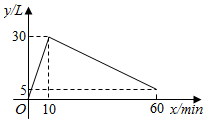 (1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.22. 已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从 地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.
(1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.22. 已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从 地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示. (1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.23. 已知A、B两地之间有一条长270千米的公路。甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止。甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示
(1)、甲车的速度为千米/时,a的值为 .(2)、求乙车出发后,y与x之间的函数关系式.(3)、当甲、乙两车相距100千米时,求甲车行驶的时间.23. 已知A、B两地之间有一条长270千米的公路。甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止。甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示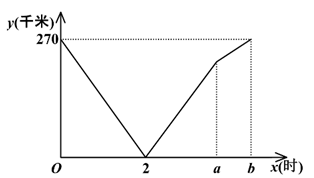 (1)、乙车的速度为千米/时,a= , b= 。(2)、求甲、乙两车相遇后y与x之间的函数关系式(3)、当甲车到达距B地70千米处时,求甲、乙两车之间的路程24. 已知 是 的反比例函数,并且当 时, .(1)、求 关于 的函数解析式;(2)、当 时,求 的值.25. 甲、乙两车分别从 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到 地,乙车立即以原速原路返回到 地,甲、乙两车距 地的路程 与各自行驶的时间 之间的关系如图所示.
(1)、乙车的速度为千米/时,a= , b= 。(2)、求甲、乙两车相遇后y与x之间的函数关系式(3)、当甲车到达距B地70千米处时,求甲、乙两车之间的路程24. 已知 是 的反比例函数,并且当 时, .(1)、求 关于 的函数解析式;(2)、当 时,求 的值.25. 甲、乙两车分别从 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到 地,乙车立即以原速原路返回到 地,甲、乙两车距 地的路程 与各自行驶的时间 之间的关系如图所示. (1)、m= , n=;(2)、求乙车距 地的路程 关于 的函数解析式,并写出自变量 的取值范围;(3)、当甲车到达 地时,求乙车距 地的路程26. 如图,抛物线 与x轴相交于 两点(点 在点 的左侧),与 轴相交于点 . 为抛物线上一点,横坐标为 ,且 .
(1)、m= , n=;(2)、求乙车距 地的路程 关于 的函数解析式,并写出自变量 的取值范围;(3)、当甲车到达 地时,求乙车距 地的路程26. 如图,抛物线 与x轴相交于 两点(点 在点 的左侧),与 轴相交于点 . 为抛物线上一点,横坐标为 ,且 .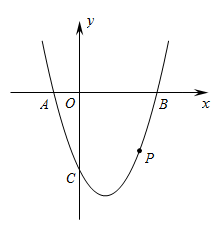 (1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .
(1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .①求 关于 的函数解析式,并写出自变量 的取值范围;
②当 时,直接写出 的面积.
27. 如图,在平面直角坐标系中,二次函数 的图象经过点 ,点 .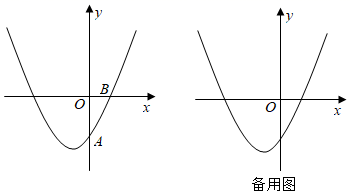 (1)、求此二次函数的解析式;(2)、当 时,求二次函数 的最大值和最小值;(3)、点 为此函数图象上任意一点,其横坐标为 ,过点 作 轴,点 的横坐标为 .已知点 与点 不重合,且线段 的长度随 的增大而减小.
(1)、求此二次函数的解析式;(2)、当 时,求二次函数 的最大值和最小值;(3)、点 为此函数图象上任意一点,其横坐标为 ,过点 作 轴,点 的横坐标为 .已知点 与点 不重合,且线段 的长度随 的增大而减小.①求 的取值范围;
②当 时,直接写出线段 与二次函数 的图象交点个数及对应的 的取值范围.
28. 在平面直角坐标系中,抛物线 (m为常数)的顶点为A .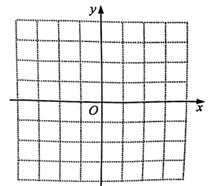 (1)、当 时,点A的坐标是 , 抛物线与y轴交点的坐标是 .(2)、若点A在第一象限,且 ,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.(3)、当 时,若函数 的最小值为3,求m的值.(4)、分别过点 、 作y轴的垂线,交抛物线的对称轴于点M、N . 当抛物线 与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C , 且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.29. 如图,在平面直角坐标系中,抛物线 与x轴正半轴交于点A,且点A的坐标为 ,过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作 于点Q;M是直线l上的一点,其纵坐标为 ,以 , 为边作矩形 .
(1)、当 时,点A的坐标是 , 抛物线与y轴交点的坐标是 .(2)、若点A在第一象限,且 ,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围.(3)、当 时,若函数 的最小值为3,求m的值.(4)、分别过点 、 作y轴的垂线,交抛物线的对称轴于点M、N . 当抛物线 与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C , 且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.29. 如图,在平面直角坐标系中,抛物线 与x轴正半轴交于点A,且点A的坐标为 ,过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作 于点Q;M是直线l上的一点,其纵坐标为 ,以 , 为边作矩形 . (1)、求b的值.(2)、当点Q与点M重合时,求m的值.(3)、当矩形 是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)、当抛物线在矩形 内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.30. 在平面直角坐标系中,函数 ( 为常数)的图象与y轴交于点A.
(1)、求b的值.(2)、当点Q与点M重合时,求m的值.(3)、当矩形 是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)、当抛物线在矩形 内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.30. 在平面直角坐标系中,函数 ( 为常数)的图象与y轴交于点A.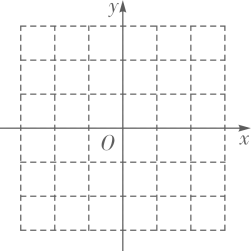 (1)、求点A的坐标.(2)、当此函数图象经过点 时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当 时,若函数 (a为常数)的图象的最低点到直线 的距离为2,求a的值.(4)、设 , 三个顶点的坐标分别为 、 、 .当函数 ( 为常数)的图象与 的直角边有交点时,交点记为点P.过点P作y轴的垂线,与此函数图象的另一个交点为 ( 与P不重合),过点A作y轴的垂线,与此函数图象的另一个交点为 .若 ,直接写出a的值.31. 已知函数y= (n为常数)(1)、当n=5,
(1)、求点A的坐标.(2)、当此函数图象经过点 时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当 时,若函数 (a为常数)的图象的最低点到直线 的距离为2,求a的值.(4)、设 , 三个顶点的坐标分别为 、 、 .当函数 ( 为常数)的图象与 的直角边有交点时,交点记为点P.过点P作y轴的垂线,与此函数图象的另一个交点为 ( 与P不重合),过点A作y轴的垂线,与此函数图象的另一个交点为 .若 ,直接写出a的值.31. 已知函数y= (n为常数)(1)、当n=5,①点P(4,b)在此函数图象上,求b的值
②求此函数的最大值
(2)、已知线段AB的两个端点坐标分别为4(2,2)、B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.(3)、当此函数图象上有4个点到x轴的距离等于4时,求n的取值范围.
-