湖北省襄阳市2021年中考数学试卷
试卷更新日期:2021-08-20 类型:中考真卷
一、单选题
-
1. 下列各数中最大的是( )A、-3 B、-2 C、0 D、12. 下列计算正确的是( )A、 B、 C、 D、3. 如图, , ,重足为 , ,则 等于( )
 A、40° B、45° C、50° D、60°4. 若二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、5. 如图所示的几何体的主视图是( )
A、40° B、45° C、50° D、60°4. 若二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、5. 如图所示的几何体的主视图是( )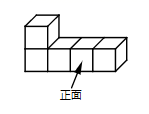 A、
A、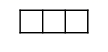 B、
B、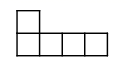 C、
C、 D、
D、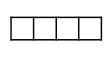 6. 随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为 ,下面所列方程正确的是( )A、 B、 C、 D、7. 正多边形的一个外角等于60°,这个多边形的边数是( )A、3 B、6 C、9 D、128. 不透明袋子中装有除颜色外完全相同的2个红球和1个白球,从袋子中随机摸出2个球,下列事件是必然事件的是( )A、摸出的2个球中至少有1个红球 B、摸出的2个球都是白球 C、摸出的2个球中1个红球、1个白球 D、摸出的2个球都是红球9. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈 尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( )
6. 随着生产技术的进步,某制药厂生产成本逐年下降.两年前生产一吨药的成本是5000元,现在生产一吨药的成本是4050元.设生产成本的年平均下降率为 ,下面所列方程正确的是( )A、 B、 C、 D、7. 正多边形的一个外角等于60°,这个多边形的边数是( )A、3 B、6 C、9 D、128. 不透明袋子中装有除颜色外完全相同的2个红球和1个白球,从袋子中随机摸出2个球,下列事件是必然事件的是( )A、摸出的2个球中至少有1个红球 B、摸出的2个球都是白球 C、摸出的2个球中1个红球、1个白球 D、摸出的2个球都是红球9. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈 尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( ) A、10尺 B、11尺 C、12尺 D、13尺10. 一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、10尺 B、11尺 C、12尺 D、13尺10. 一次函数 的图象如图所示,则二次函数 的图象可能是( )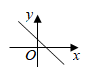 A、
A、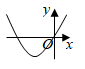 B、
B、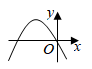 C、
C、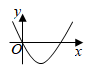 D、
D、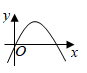
二、填空题
-
11. 据统计,2021年“五·一”劳动节小长假期间,襄阳市约接待游客2270000人次.数字2270000用科学记数法表示为.12. 不等式组 的解集是.13. 中国象棋文化历史久远.在图中所示的部分棋盘中,“馬”的位置在“---”(图中虚线)的下方,“馬”移动一次能够到达的所有位置已用“●”标记,则“馬”随机移动一次,到达的位置在“---”上方的概率是.
 14. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .
14. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .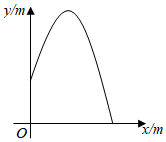 15. 点 是 的外心,若 ,则 为.16. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
15. 点 是 的外心,若 ,则 为.16. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,建筑物 上有一旗杆 ,从与 相距 的 处观测旗杆项部 的仰角为52°,观测旗杆底部 的仰角为45°,求旗杆 的高度(结果保留小数点后一位.参考数据: , , , ).
 19. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:
19. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:( 1 )收集数据从该校七.八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
( 2 )整理、描述数据按如下分段整理描述样本数据:
分数
人数
年级
七年级
4
6
2
8
八年级
3
4
7
( 3 )分析数据两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
33.2
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分,同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”):
③从样本数据分析来看,分数较整齐的是年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有人的分数不低于95分.
20. 如图, 为 的对角线. (1)、作对角线 的垂直平分线,分别交 , , 于点 , , (尺规作图,不写作法,保留作图痕迹);(2)、连接 , .求证:四边形 为菱形.21. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象
(1)、作对角线 的垂直平分线,分别交 , , 于点 , , (尺规作图,不写作法,保留作图痕迹);(2)、连接 , .求证:四边形 为菱形.21. 小欣在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质.其研究过程如下:(1)、绘制函数图象①列表:下表是 与 的几组对应值,其中 ▲ ;
…
-4
-3
-2
0
1
2
…
…
-1
=2
-3
3
2
…
②描点:根据表中的数值描点 ,请补充描出点 ;
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
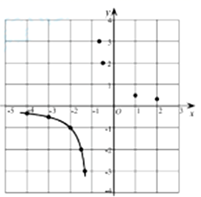 (2)、探究函数性质
(2)、探究函数性质判断下列说法是否正确。
①函数值 随 的增大而减小:
②函数图象关于原点对称:
③函数图象与直线 没有交点.
22. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , . (1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.23. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
(1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.23. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:进价(元/斤)
售价(元/斤)
鲢鱼
5
草鱼
销量不超过200斤的部分
销量超过200斤的部分
8
7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)、求 , 的值;(2)、老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼 斤(销售过程中损耗不计).①分别求出每天销售鲢鱼获利 (元),销售草鱼获利 (元)与 的函数关系式,并写出 的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低 元,草鱼售价全部定为7元斤,为了保证当天销售这两种鱼总获利 (元)的最小值不少于320元,求 的最大值.
24. 在 中, , , 是边 上一点,将 沿 折叠得到 ,连接 . (1)、特例发现:如图1,当 , 落在直线 上时,
(1)、特例发现:如图1,当 , 落在直线 上时,①求证: ;
②填空: 的值为 ▲ ;
(2)、类比探究:如图2,当 , 与边 相交时,在 上取一点 ,使 , 交 于点 .探究 的值(用含 的式子表示),并写出探究过程;(3)、拓展运用:在(2)的条件下,当 , 是 的中点时,若 ,求 的长.25. 如图,直线 与 , 轴分别交于 , ,顶点为 的抛物线 过点 . (1)、求出点 , 的坐标及 的值;(2)、若函数 在 时有最大值为 ,求 的值;(3)、连接 ,过点 作 的垂线交 轴于点 .设 的面积为 .
(1)、求出点 , 的坐标及 的值;(2)、若函数 在 时有最大值为 ,求 的值;(3)、连接 ,过点 作 的垂线交 轴于点 .设 的面积为 .①直接写出 关于 的函数关系式及 的取值范围;
②结合 与 的函数图象,直接写出 时 的取值范围.