山东省青岛市城阳区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{- 3} + a^{3} = a^{0}$ B、（a³）³=a⁶ C、（ab）²=ab² D、a³·a²=a⁵

查看试题解析
2. 下列图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
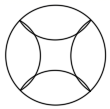3. 下列事件属于必然事件的是（）

A、任意买一张电影票，座位号是3的倍数 B、任意掷一枚质地均匀的骰子，掷出的点数是偶数 C、画一个三角形，其内角和是180° D、12人中至少有2人的生日在同一个月

查看试题解析
4. 如图，某地用图像记录了2月份某天24小时的温度随时间变化的情况，请你仔细观察图像，根据图中提供的信息，判断下列描述与图像不符合的是（）

A、16时的温度约为1℃ B、在-3℃以上的时间约为16小时 C、温度是-1℃的时刻只有10时 D、温度最低的时刻是4时

查看试题解析
5. 如图是一个可以自由转动的转盘，转动转盘，当转盘停止时，指针落在蓝色区域的概率是（）

A、 $\frac{25}{36}$ B、 $\frac{1}{3}$ C、 $\frac{11}{36}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，已知AB//CD ， EH⊥CD于点H ， ∠HEF=37°，则∠AEG=（）

A、37 B、53 C、63 D、143

查看试题解析
7. 如图，在△ABC中，已知点D、E、F分别是BC、AD、BE上的中点，且△BED的面积为3cm² ，则△ABC的面积为（）cm² ．

A、24 B、12 C、9 D、6

查看试题解析
8. 如图，大正方形的边长为 $m$ ，小正方形边长为n ，若用a、b表示四个全等小正方形的两边长（a>b），观察图案，以下关系式正确的是（）

① $a b = \frac{m^{2} - n^{2}}{4}$ ②a+b=m③ $a^{2} - b^{2} = m n$ ④ $2 a^{2} - 2 b^{2} = m^{2} - n^{2}$

A、①②③④ B、②③④ C、①②③ D、①②④

查看试题解析

二、填空题

9. 计算： ${(\frac{1}{5})}^{- 1} - {(π - 2)}^{0} =$

查看试题解析
10. 小华用三根木棒搭一个三角形，其中两根木棒的长度分别为10cm和2cm，第三根木棒的长度为偶数，则第三根的长度是cm．

查看试题解析
11. 某花的花粉直径约为0.0000009288米，则数据0.0000009288可以用科学技术发表示为．

查看试题解析
12. 如图，在△ABC中，已知DE//BC ， ∠1=∠2，∠BEC=96°，则∠FGE=°

查看试题解析
13. 如图，BD平分∠ABC交AC于点D ，沿DE折叠BC ，使B、C两点重合．已知∠C=35°，则∠A=°

查看试题解析
14. 一辆汽车邮箱内有油62升．如果设邮箱内剩油量为y（升），行驶路程为x（千米），则y随x的变化而变化：

行驶路程x（千米）

100

200

300

400

油箱内剩油量y（升）

50

38

26

14

请根据表格中的数据写出y（升）与x（千米）之间的关系式y= ．

查看试题解析
15. 如图，把一副七巧板按如图进行1~7编号，1~7号分别对应着七巧板的七块，如果编号5对应的面积等于5cm² ，则由这幅七巧板拼得的“房子”的面积等于cm² ．

查看试题解析
16. 如图，在△ABC中，∠ACB=90°，CE⊥AB于点E ， AD=AC ， AF平分∠CAB交CE于点F ， DF的延长线交AC于点G ，以下结论：①DF//BC；②FG=FE；③∠ACF=∠B；④EF+CG>CF ．其中正确的有（填正确结论的序号）

查看试题解析

三、解答题

17.

(1)、已知：线段a ， ∠α，∠β．
求作：△ABC ，使AB=a ， ∠A=α，∠B=β（请用直尺、圆规做图，不写作法，但要保留作图痕迹）

(2)、如图，在长度为1个单位的小正方形组成的网格中，点A ， B ， C在小正方形的顶点上，在图中画出与△ABC关于直线l成轴对称的△A'B'C' ．

查看试题解析
18. 计算

(1)、 ${(- x^{2} y)}^{3} \div (- \frac{1}{3} x y^{3})$

(2)、 $(- \frac{1}{4} x - 3 y) (- \frac{1}{4} x + 3 y)$

(3)、 $(3 x - 1) (x + 2) + {(x - 3)}^{2}$

(4)、 ${(a - b)}^{3} \div (a - b) + 2 a b$

查看试题解析
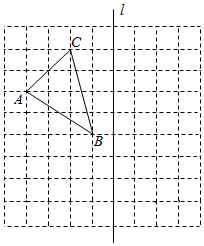19. 先化简，后求值： $[(2 x y - 3) (2 x y + 3) - 5 x^{2} y^{2} + 9] \div x y$ 其中x=35，y= $\frac{1}{7}$

查看试题解析
20. 某校举行“青春心向党．建功新时代”演讲比赛．每班选拔一人参加．七年级（1）班的小丽和小华表现都很优秀，现在打算从2位同学中任选1人参加学校演讲比赛．设计了如下游戏规则：把5个完全相同的乒乓球标上数字1，2，3，4，5然后放到一个不透明的袋子中，一个人从袋中随机摸出一个球记下数字．若摸出的球上的数字为奇数，则小丽去；若摸出的球上的数字为偶数，则小华去．

(1)、小丽去的概率是；

(2)、小华去的概率是；

(3)、这个游戏规则是否公平？请说明理由．

查看试题解析
21. 已知：∠DEC+∠C=180°，DE平分∠ADF ， ∠F=∠1．求证：∠B=∠C ．

查看试题解析
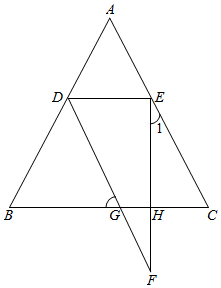22. 某校需印制导学案，有甲、乙两家印刷厂可供选择．除按印数收取印刷费外，甲印刷厂还需收取制版费，而乙印刷厂不需要制版费．两印刷厂的费用y（元）与印刷份数x（份）之间的关系如图所示：

(1)、描述甲印刷厂费用y（元）与印刷份数x（份）之间关系的图像是．（填y₁或y₂）

(2)、直接写出乙印刷厂费用y_乙（元）与印刷份数x（份）之间关系式是．

(3)、若该校印刷的数量为120份，则他去厂印刷的花费少；

(4)、若该校印刷的花费了280元，则他去厂印刷的数量多．

查看试题解析
23. 已知： Rt△ABC中，∠CBA=90°，AB=BC ， Rt△DBE中，∠DBE=90°，DB=EB ，连接DC ， AE ，延长AE交DC于点F ．

求证：

(1)、△AEB≌△CDB；

(2)、∠CFA=90°．

查看试题解析
24. 提出问题：在不透明口袋中放入16种颜色的小球（小球除颜色外完全相同）各50个，现要确保从口袋中随机摸出的小球至少有10个是同色的，则最少需要摸出多少个小球？
建立模型：为解决上面的“问题”，我们先建立并研究下面从口袋中摸球的数学模型：

(1)、在不透明的口袋中装有红、黄、蓝三种颜色的小球各50个（除颜色外完全相同），现在要确保从口袋中随机摸出的小球至少有4个是同色的，则最少需要摸出多少个小球？为了找到解决问题的办法，我们可以把上述问题简单化：
①我们首先考虑最简单的情况：既要确保从口袋中摸出的小球至少有2个是同色的，则最少需摸出多少个小球？

假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需要再从袋中摸出1个小球就可确保至少有2个小球同色，即最少需要摸出小数的个数是：1+3=4；

②若要确保从口袋中摸出的小球至少有3个是同色的呢？

我们只需要在①的基础上，再从袋中摸出3个小球，就可以确保至少有3个小球同色，即最少需摸出小球的个数是：1+3×2=7

③若要确保从口袋中摸出的小球至少有4个小球同色，即最少需要摸出小球的个数是：1+3×3=10

④若要确保从口袋中摸出的小球至少有a个是同色的呢？即最少需要摸出小球的个数是．

(2)、模型拓展一：在不透明的口袋中装有红、黄、蓝、白、绿、紫六种颜色的小球各50个（除颜色外完全相同），现在从袋中随机摸球：
①若要确保摸出的小球至少有2个同色，则最少需摸出小球的个数是；

②若要确保摸出的小球至少有12个同色，则最少需摸出小球的个数是；

③若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是；

(3)、模型拓展二：在不透明口袋中装有n中颜色的小球各50个（除颜色外完全相同），现从袋中随机魔球：
①若要确保摸出的小球至少有3个同色，则最少需摸出小球的个数是

②若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是．

(4)、问题解决：在不透明口袋中放入16种颜色的小球（小球除颜色外完全相同）各50个，现要确保从口袋中随机摸出的小球至少有10个是同色的，则最少需摸出小球的个数是．

查看试题解析
25. 如图，AB=36米，CB⊥AB于点B ， EA⊥AB于点A ，已知CB=24米，点F从点B出发，以3米/秒的速度沿BA向点A运动（到达点A停止运动），设点F的运动时间为t秒．

(1)、如图，S_△BFC= ．（用t的代数式表示）

(2)、点F从点B开始运动，点D同时从点A出发，以x米/秒的速度沿射线AE运动，是否存在这样x的值，使得△AFD与△BCF全等？若存在，请求出x的值；若不存在，请说明理由

查看试题解析

行驶路程x（千米）	100	200	300	400
油箱内剩油量y（升）	50	38	26	14