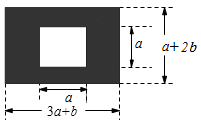
内蒙古自治区包头市青山区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-19 类型:期末考试
一、单选题
-
1. 下列图形不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在下列运算中,计算正确的是( )A、 B、 C、 D、3. 下列事件为必然事件的是( )A、打开电视机,它正在播广告 B、抛掷一枚硬币,一定正面朝上 C、投掷一枚普通的正方体骰子,掷得的点数小于7 D、某彩票的中奖机会是1%,买1张一定不会中奖4. 新型冠状病毒的直径约为125纳米(1纳米 米),125纳米用科学记数法表示为( )米.A、 B、 C、 D、5. 下列乘法公式的运用,错误的是( )A、 B、 C、 D、6. 将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
2. 在下列运算中,计算正确的是( )A、 B、 C、 D、3. 下列事件为必然事件的是( )A、打开电视机,它正在播广告 B、抛掷一枚硬币,一定正面朝上 C、投掷一枚普通的正方体骰子,掷得的点数小于7 D、某彩票的中奖机会是1%,买1张一定不会中奖4. 新型冠状病毒的直径约为125纳米(1纳米 米),125纳米用科学记数法表示为( )米.A、 B、 C、 D、5. 下列乘法公式的运用,错误的是( )A、 B、 C、 D、6. 将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )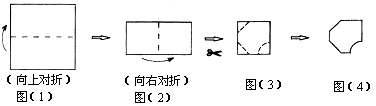 A、
A、 B、
B、 C、
C、 D、
D、 7. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、
7. 小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )A、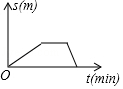 B、
B、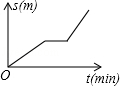 C、
C、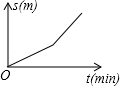 D、
D、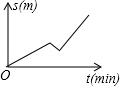 8. 将一把直尺和一块含 角的直角三角板按如图所示方式摆放,其中 , .若 ,则 的度数为( )
8. 将一把直尺和一块含 角的直角三角板按如图所示方式摆放,其中 , .若 ,则 的度数为( ) A、 B、 C、 D、9. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°10. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( )
A、 B、 C、 D、9. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°10. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( ) A、①②③④ B、①②③ C、②④ D、①③
A、①②③④ B、①②③ C、②④ D、①③二、填空题
-
11. = .12. 在一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球,记下颜色后,再放回暗箱,通过大量的重复试验后发现,摸到红球的频率稳定在25%.那么估计a大约有 个.13. 两同心圆,小圆半径为2cm,大圆半径为4cm,则一只蚊子落在同心圆的黑色区域内的概率为 .
 14. 任意写出一个三位数(三位数字都不相同),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大数减去最小数,得到差,不断重复这个过程,最后一定会得到相同的结果,这个结果是 .15. 如图,分割边长10cm的正方形,制作一副七巧板,图2是拼成的“小房子”,其中阴影部分的面积为cm2 .
14. 任意写出一个三位数(三位数字都不相同),重新排列各位数字,使其组成一个最大的数和一个最小的数,然后用最大数减去最小数,得到差,不断重复这个过程,最后一定会得到相同的结果,这个结果是 .15. 如图,分割边长10cm的正方形,制作一副七巧板,图2是拼成的“小房子”,其中阴影部分的面积为cm2 . 16. 如图所示,AD、CE、BF是△ABC的三条高,AB=6,BC=5,AD=4,则CE= .
16. 如图所示,AD、CE、BF是△ABC的三条高,AB=6,BC=5,AD=4,则CE= . 17. 如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 .
17. 如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则矩形MNPQ的面积是 .
三、解答题
-
18. 如图,如果AD∥BC , AD=BC , AC与BD相交于O点,则图中的全等三角形一共有对.
 19. 计算:(1)、(﹣1)2020+(﹣ )﹣2﹣(3.14﹣π)0;(2)、先化简,再求值:[(a﹣b)2﹣(a﹣2b)(2a+5b)+(a+b)(a﹣b)]÷2b , 其中a=1, .20. 某校七年级学生到野外活动,为测量一池塘两端A , B的距离,甲、乙、丙三位同学分别设计出如下几种方案:
19. 计算:(1)、(﹣1)2020+(﹣ )﹣2﹣(3.14﹣π)0;(2)、先化简,再求值:[(a﹣b)2﹣(a﹣2b)(2a+5b)+(a+b)(a﹣b)]÷2b , 其中a=1, .20. 某校七年级学生到野外活动,为测量一池塘两端A , B的距离,甲、乙、丙三位同学分别设计出如下几种方案: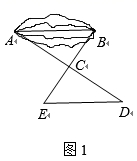
甲:如图①,先在平地取一个可直接到达A , B的点C , 再连接AC , BC , 并分别延长AC至D , BC至E , 使DC=AC , EC=BC , 最后测出DE的长即为A , B的距离.
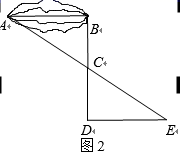
乙:如图②,先过点B作AB的垂线,再在垂线上取C , D两点,使BC=CD , 接着过点D作BD的垂线DE , 交AC的延长线于点E , 则测出DE的长即为A , B的距离.
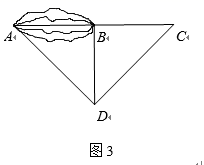
丙:如图③,过点B作BD⊥AB , 再由点D观测,在AB的延长线上取一点C , 使∠BDC=∠BDA , 这时只要测出BC的长即为A , B的距离.
(1)、以上三位同学所设计的方案,可行的有;(2)、请你选择一可行的方案,说说它可行的理由.21. 下面网格都是由边长为 的小正方形组成,观察如图三个图案(阴影部分),回答下列问题: (1)、请写出这三个图案的至少两个共同特征;(2)、请在图④中设计一个图案,使它具备你所写出的特征.22. 如图,现有一个均匀的转盘被平均分成六等份,分别标有 这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,不记,重转).
(1)、请写出这三个图案的至少两个共同特征;(2)、请在图④中设计一个图案,使它具备你所写出的特征.22. 如图,现有一个均匀的转盘被平均分成六等份,分别标有 这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,不记,重转). (1)、转动转盘,转出的数字大于3的概率是多少;(2)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
(1)、转动转盘,转出的数字大于3的概率是多少;(2)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?(注:要求写出各种可能情况)